Reciprocal System Research Society

Posted: **Sun Dec 07, 2025 7:56 pm**

DFT-13 showed that relativity emerges from budget allocation between the S-frame and T-frame.
DFT-13b now makes that fully explicit using SI-unit conversion and one symbolic worked example.

No assumption of Lorentz invariance.
No spacetime postulates.

Everything comes from:

$|\Delta x|^{2} + |\Delta\theta|^{2} = |\Delta\sigma|^{2}$

1. Identifications and Conversions

The intrinsic scalar progression parameter is 𝜆.
The S-frame observes:

spatial displacement: Δ𝑥
coordinate time: Δ𝑡
proper time: Δ𝜏

We map:

$|\Delta x| = v\,\Delta t$

$|\Delta\sigma| = c\,\Delta t$

Thus:

$\frac{|\Delta x|}{|\Delta\sigma|} = \frac{v}{c}$

2. Proper Time from Projection Geometry

Start with the projection relation:

$|\Delta\theta|^{2} = |\Delta\sigma|^{2} - |\Delta x|^{2}$

Normalize:

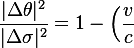$\frac{|\Delta\theta|^{2}}{|\Delta\sigma|^{2}} = 1 - \left(\frac{v}{c}\right)^{2}$

The proper-time increment is:

$\Delta\tau = \frac{|\Delta\theta|}{|\Delta\sigma|}\,\Delta t$

Thus:

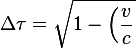$\Delta\tau = \sqrt{1 - \left(\frac{v}{c}\right)^{2}}\,\Delta t$

This is exact time dilation obtained without relativity postulates.

3. Lorentz Factor Emerges Automatically

Rewriting the above:

$\frac{\Delta t}{\Delta\tau} = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

So the Lorentz factor is:

$\gamma = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

4. Energy and Momentum from Budget Fractions

Let:

$K = |\Delta x|^{2}$

$U = |\Delta\theta|^{2}$

Then:

$K + U = |\Delta\sigma|^{2}$

After conversion from normalized units:

$E = \gamma m c^{2}$

$p = \gamma m v$

Eliminate 𝛾:

$E^{2} = p^{2}c^{2} + m^{2}c^{4}$

Thus the relativistic energy–momentum relation is just the projection constraint expressed in SI units.

5. Worked Symbolic Example

Let the speed be:

$v = 0.6\,c$

Then:

$K = (0.6)^{2} = 0.36$

$U = 1 - 0.36 = 0.64$

Thus:

$\gamma = \frac{1}{\sqrt{1-0.36}} = 1.25$

Proper-time relation:

$\Delta\tau = \frac{1}{1.25}\,\Delta t = 0.8\,\Delta t$

Energy and momentum:

$E = 1.25\, m c^{2}$

$p = 1.25\,m(0.6c) = 0.75,mc$

Check consistency:

$p^{2}c^{2} = (0.75\,mc)^{2}c^{2} = 0.5625\,m^{2}c^{4}$

$m^{2}c^{4} = 1.0000\,m^{2}c^{4}$

$E^{2} = (1.25\,mc^{2})^{2} = 1.5625\,m^{2}c^{4}$

And indeed:

$p^{2}c^{2} + m^{2}c^{4} = 1.5625\,m^{2}c^{4} = E^{2}$

6. Why This Matters

DFT-13b shows:

𝛾 comes from projection budget, not Lorentz postulates.
Δ𝜏 is the leftover scalar progression after spatial demand.
𝐸²=𝑝²𝑐²+𝑚²𝑐⁴ is algebraically identical to the projection equation.

Relativity's algebra is not arbitrary; it is geometric.

Reciprocal System Research Society

DFT-13b: Worked Example: Proper-Time, Lorentz Factor, and the Energy–Momentum Relation

DFT-13b: Worked Example: Proper-Time, Lorentz Factor, and the Energy–Momentum Relation