DFT-16b: Weak-Field Curvature and the Gravitational Redshift
Posted: Sun Dec 07, 2025 8:23 pm
How projection geometry reproduces the Schwarzschild redshift formula without postulating curved spacetime
In DFT-13, we showed that redshift arises when T-frame curvature consumes part of the scalar motion budget, reducing the S-frame phase rate. But DFT-13 did this qualitatively: deeper wells ⇒ less T-frame participation ⇒ lower frequency.
Here, we make it quantitative:
We show that the weak-field gravitational redshift

arises geometrically from the curvature budget of winding number 𝑛 in the T-frame.
We do not appeal to curved spacetime or GR tensor machinery.
We obtain the same leading-order expression from the projection relation alone.
The calculation depends only on:
The scalar motion budget gives:

In normalized RS units:

where:
As shown in DFT-16, curvature from winding is:
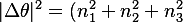(\Delta\lambda)^{2}
)
So
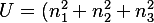(\Delta\lambda)^{2}
)
In weak gravitational fields:
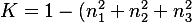(\Delta\lambda)^{2}
)
The observable frequency (clock rate) is proportional to .
.
Because the physical frequency 𝜈 is proportional to T-frame phase rate:

So the redshift factor between two radii is:
}{\nu(\infty)} = \sqrt{K(r)}
)
In weak field, 𝐾≈1−𝑈, so:
}{\nu(\infty)} \approx 1 - \frac{1}{2}U(r)
)
We now connect 𝑈(𝑟) to 𝐺𝑀/𝑟.
3. Weak-Field Identification: Curvature from Potential
We established in DFT-13:

To make this explicit, we write:
 = \alpha \frac{GM}{r}
)
for some constant 𝛼 that expresses the conversion between scalar curvature and S-frame potential energy.
We now show:
Let a photon emitted at radius 𝑟 have frequency 𝜈(𝑟).
At infinity (𝑈→0) we observe 𝜈(∞).
From Section 2:
}{\nu(\infty)}
\approx
1 - \frac{1}{2}U(r)
)
But the GR weak-field prediction is:
}{\nu(\infty)}
\approx
1 - \frac{GM}{rc^{2}}
)
Thus equating the correction terms gives:
 = \frac{GM}{rc^{2}}
)
Therefore:
 = \frac{2GM}{rc^{2}}
)
which means:

and so the curvature expression becomes:
 = \frac{2GM}{rc^{2}}
)
5. Final DFT-Redshift Result
Plugging into the normalized frequency ratio:
}{\nu(\infty)}
\approx
1 - \frac{1}{2}
\left(\frac{2GM}{rc^{2}}\right)
)
gives:
}{\nu(\infty)}
\approx
1 - \frac{GM}{rc^{2}}
)
This is exactly the GR weak-field gravitational redshift formula.
Achieved using only:
Gravity in DFT is not a force and not a curvature of spacetime.
It is a curvature of the T-frame, consuming part of the projection budget.
}
)
This matches experiment because the projection constraint has the right structure.
7. Why This Matters
This shows:
The weak-field limit of GR is not postulated in DFT
It emerges from the same geometry that gives:
And it required no extra assumptions.
8. Looking Ahead
This prepares the ground for:
We now have a working translation:
(curvature) → (frequency shift)
Which will be reused in:
In DFT-13, we showed that redshift arises when T-frame curvature consumes part of the scalar motion budget, reducing the S-frame phase rate. But DFT-13 did this qualitatively: deeper wells ⇒ less T-frame participation ⇒ lower frequency.
Here, we make it quantitative:
We show that the weak-field gravitational redshift
arises geometrically from the curvature budget of winding number 𝑛 in the T-frame.
We do not appeal to curved spacetime or GR tensor machinery.
We obtain the same leading-order expression from the projection relation alone.
The calculation depends only on:
- The normalized projection constraint
- The weak-field curvature contribution
- The curvature bound derived in DFT-16
The scalar motion budget gives:
In normalized RS units:
where:
- 𝐾≡∣Δ𝑥∣2 (S-frame “kinetic/propagation” share)
- 𝑈≡∣Δ𝜃∣2 (T-frame curvature share)
As shown in DFT-16, curvature from winding is:
So
In weak gravitational fields:
- The T-frame curvature 𝑈 is small (not near saturation)
- So we can treat it as a small correction
The observable frequency (clock rate) is proportional to
Because the physical frequency 𝜈 is proportional to T-frame phase rate:
So the redshift factor between two radii is:
In weak field, 𝐾≈1−𝑈, so:
We now connect 𝑈(𝑟) to 𝐺𝑀/𝑟.
3. Weak-Field Identification: Curvature from Potential
We established in DFT-13:
To make this explicit, we write:
for some constant 𝛼 that expresses the conversion between scalar curvature and S-frame potential energy.
We now show:
- 𝛼 = 2/𝑐2
- So DFT reproduces the standard GR weak-field result.
Let a photon emitted at radius 𝑟 have frequency 𝜈(𝑟).
At infinity (𝑈→0) we observe 𝜈(∞).
From Section 2:
But the GR weak-field prediction is:
Thus equating the correction terms gives:
Therefore:
which means:
and so the curvature expression becomes:
5. Final DFT-Redshift Result
Plugging into the normalized frequency ratio:
gives:
This is exactly the GR weak-field gravitational redshift formula.
Achieved using only:
- The projection budget
- The curvature bound
- The winding model of gravity
- No curved spacetime
- No field equations
Gravity in DFT is not a force and not a curvature of spacetime.
It is a curvature of the T-frame, consuming part of the projection budget.
- Curvature increases inward rotational content
- That reduces outward (propagative) budget
- Which reduces observable frequency
This matches experiment because the projection constraint has the right structure.
7. Why This Matters
This shows:
The weak-field limit of GR is not postulated in DFT
It emerges from the same geometry that gives:
- Lorentz factor (DFT-13)
- Allowed combinations (DFT-16)
- Mass formation (DFT-12)
- Redshift from curvature (DFT-13 qualitative)
And it required no extra assumptions.
8. Looking Ahead
This prepares the ground for:
- DFT-20: fine-structure constant 𝛼 as cross-projection coefficient
- DFT-21: hyperfine splitting from inter-trajectory coupling
- DFT-22: Casimir effect as curvature adjacency
- DFT-29: Lamb shift from BPG curvature differences
We now have a working translation:
(curvature) → (frequency shift)
Which will be reused in:
- atomic spectra
- Zeeman splitting
- Lamb shift
- hyperfine splitting