**************************
ADDENDUM 04/15/2020
**Prototype Universe**
.........in progress.........
Let Φπ² be a universe composed of an incessant relationship between Φ and π².π = √(8√5-8) or 4√Φ
π² = (8√5-8) or 16/Φ
Φ = (π+π√5)/2π
Φ² = (3π+π√5)/2π
1 = 2π/2π
Construct:
→ ∞ velocity = v = s³/t ↔ (st)² ↔ t³/s = e = energy ∞ ←
˟π ≠ 3.1415926...R/S System of Theory Postulates:
1. The universe is composed of one component, motion, existing in three dimensions, in discrete units, and with two reciprocal aspects, space and time.
2. The universe conforms to the relations of ordinary mathematics, its primary magnitudes are absolute, and its geometry is Projective.
(long-standing human "approximation" error,
π is naturally coupled to Φ via 4/√Φ=3.1446055...)
___________________________________________________
˟proposed barrier to any/all present-day scientific "progression".
Note (8√5-8) is an "octave" passing through the Φ terminus √5.
"Em-pi-phi":
√(8√5-8) = π
(8√5-8) = π²
(π√5±π)/2π = (Φ - 1), Φ
(3π+π√5)/2π = (Φ + 1), Φ²
Let unity be 1.
2π/2π = c ...."Datum..."
π = 4/√Φ ...."Enlighten..."
π² = 16/Φ ..."Empower..."
16 = Φπ² ...."Rationalize..."
e = MC² ....."Compare..."
1 = Φπ²/16 ...... "Unify..."
∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞bperet wrote: ↑Tue Oct 23, 2007 10:50 pm ...so they invent units for a "universal constant", G. In the RS, there should be no "universal constants" outside of unity. If there are, then we missed something, which is obvious in this case.
Right now, I don't have a definitive answer, but I'll post my research and thoughts on the subject. Please feel free to contribute any ideas you may have.
1 = Φπ²/16
∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞
viz.
√1 = +1, -1
+1 = Unity
-1 = Not Unity
-(-1) = Not Not Unity = Unity = +1
√+1 = +1 (real)
√-1 = i (imaginary)
viz. 'real' and 'imaginary' axes both implicitly and explicitly concerning unity and/or not.
Concerning Unity:
Φ = 1.618... UNIVERSAL PROGRESSION (concerns UNITY)
Φ² = 2.618... LOCAL DISCRETION (terminus of absolute magnitude(s) to+∞-from UNITY)
Φ³ = 4.236... UNIVERSAL GRAVITATION (concerns DISPLACEMENT(S) from UNITY)

.....Φ² ± Φ = Φ³, 1.....
"(All) LOCAL DISCRETION(s) to/from (all) PROGRESSION
is equal to (all) UNITY and/or (all) GRAVITATION(s)."
Discretely real (and imaginary) number (unit) axes:
256 = x⁴ + 16x²
x = 4/√Φ = π
x = ±√9.88854381999... viz. ±√1 as a real number axis 'r'
x = ±i√25.88854381999... viz. ±i√16 as an imaginary number axis 'i'
x² = 9.88854381999... = π² = (-8+8√5) RS¹ The late Dewey B. Larson ("yang" thinker).
RS² The late Bruce Peret et al. ("yin" contributor).
RS³ Unification (in progress...)
**************************
**************************
Original post:
______________________________________________________
Due to the circumstances at the time of this post, I am placing this here
should it be picked up and/or developed further by someone in the future,
as presently it is difficult to dialogue directly with other members for review.
After reviewing the work of Miles Mathis,
in particular his finding that π = 4
in all kinematic situations:
http://milesmathis.com/pi3.html (short version)
http://milesmathis.com/pi2.html (long version)
With a primer from Ken Wheeler regarding the importance of ΦAbstract: I show that in all kinematic situations, π is 4... this paper applies to kinematic situations, not to static or geometric situations. I am analyzing the equivalent of an orbit, which is caused by motion and includes the time variable. In that situation, π becomes 4. I will also remind you this is not just a theory: it has been indicated by many mainstream experiments, including rocketry tests and quantum experiments...
-Miles Mathis, The Extinction of π
and how it intimately relates to '1', much of which is relevant to
what follows:
https://www.youtube.com/watch?v=6hy5ItrH5MM
It occurred to me that because we live in a universe of motion (default: kinematic), π must always somehow relate to 4.
There is a rudimentary difference between a length and a distance: the former is static with no implicit motion, whereas
the latter implies time as a constituency: some space over some time, thus v = s/t implies a kinematic π by default.
Excusing Mathis' missing the connection to √Φ, both static (geometric) and dynamic (kinematic) π can be recovered:
Begin with a circle whose diameter is √5 and place two unit squares
inside the circle side-by-side, either horizontally or vertically (latter shown)
and connect any two opposite corners (shown AB) thus finding the describing line
to be √5. Extend AB by +1 unit (BC shown) and find the middle (D)
such to satisfy (1+√5)/2 shown as (BC + AB) / (D).
Find that by rotating AC about the origin, point D draws a related circle
which "kisses" the corresponding unit square 4 times equidistantly,
thus a precise π can be found (without the need for approximation)
expressed as an integer ratio of 4/√Φ.
wherein if:
4/√Φ = π then
16/Φ = π² thus
Φπ² = 16
See here for the source that lead to the connection:
https://www.youtube.com/watch?v=d-EjoQp9ug8
**************************
**************************
ADDENDUM 04/15/2020
The author of this post has not, does not, and shall not lay claim to the discovery re: π=4/√Φ.
This relationship was first encountered by myself according to the work of Jain via his public video lectures
and whose work can be found here: https://www.jain108.com/.
Regretfully I have not had the opportunity to read any of Jain's published works,
which includes a series on phi (containing the concerned π "correctional code"),
however was immensely pleased to learn of his having also found the following:
f(x) = x⁴ + 16x² - 256
Which relates to the difference of '16' allowing for
the conjoining of the real/imaginary number axes.
x = ±√9.88854381999...
x = ± i√25.88854381999...
π² = 9.88854381999...
I have given Jain an open-ended invitation to join the forums and interact freely,
thus submit this addentum is intended to clarify the origination of the π=4/√Φ correction,
and give Jain the freedom to participate (or not) in the progression towards RS³.
**************************
**************************
Thus, rather than π being transcendental,
π as 4/√Φ is a root of:
f(x) = x⁴ - 16x² - 256
whereas Φ is known to be the solution to
x² - x - 1 = 0... however unity concerns 1, not 0 (null), thus
x² - x = 1
What follows from this re-coupling of Φ to π is:
what Φ is to 1D yang {space}, π² is to 2D yin {time}
thus 16=Φπ² re-captures the co-operative relationship
between space and time: multiplicative reciprocal aspects of motion
viz. 1 = Φπ²/16 × 16/Φπ² = 1
We should thus expect to find of the former: two real and two imaginary roots (ie. an axes)
as pairs of conjugates (+/-) co-mutually concerning unity '1' in some relation to '16'.
See here for the roots, noting the '888'
beginning from the tenth decimal
(perhaps of esoteric interest to some): (Note: this finding has implications for the Reimann Hypothesis
as outlined here: https://reciprocal.systems/phpBB3/viewt ... =680#p4031).
Emphasis added: Φπ² = 16 implies π² = 16/Φ and Φ = 16/π²,bperet wrote: ↑Wed Feb 25, 2009 3:12 pm The 4x4 matrix contains the various speeds of the three, scalar dimensions along the diagonal, with transforms for rotation (turn) and shift (translation) multiplied in, as complex quantities. One interesting result is that spatial location is altered by temporal location, and vice versa, and that no single scalar dimension is directly represented in the system, as Larson claimed, but it is the net motion of all three dimensions that is represented. (Not a problem most of the time, since two of the dimensions are usually at unity--identity--and have no effect).
hence one altering the other and vice versa, however still hinging on 16, thus:
Bruce is right: 1 of 16 cannot be variable because '16' is inclusive of the universal datum of '1'
(thus the same is true for the posited 2x2 transcendental universal axes to follow),
the presence of which is needed for the rest of the matrix to be discernible from it,
just as unity would be required to allow discernment of all that is displaced from unity.
Thus posited: symmetrically about the 4x4 matrix sits a single transcendental axes of '4' composed of 2x2 null binaries:
all+/-not denoted {alpha/omega} and causation+/-cessation denoted {beg/end}, each pair being a conjugate binary (+/-),
the transcendental nature of which owing to the axes being wholly space- and time-invariant,
thus must rest in/of and/or as '1' as well as being '4' (if indeed both transcendental and universal).
This must be true because no non-transcendental axes can ever be used to transcend a displaced body(s) beyond
the limitation/boundary of the axes itself. Because this axes transcends beyond space and time, it must follow that all
caused bodies contains this axes intrinsic to their own composition. In other words: all displaced bodies have local to them,
as part of their own constituency, a transcending axes immutably concerning unity at all times from all places.
Here is the postulated transcendental axes: Universally Bestowed: {ALL∞NOT}{CAUSATION∞CESSATION}
Locally Employed: {ALPHA+∞-OMEGA}{BEG+∞-END}
Photon: {ALL∞NOT}=birotation/biorientation, {CAUSATION∞CESSATION}=null/false (because no displacement)
All Else: {ALPHA∞OMEGA}=true and implicitly/explicitly concerns {ALL∞NOT}, {BEG∞END}=true (displacement)
The birotation is related to the axes having two valid polar 'states' and polar 'orientations'
according to the axis of {ALL∞NOT} and concerning the local axis of {BEG∞END} as conjunct
such that the latter is subject to/of the former (as in the case of the counting Fib. sequence approaching Φ):
{ALL∞NOT}{BEG∞END} (all displaced, all not displaced).
This begs a brief mention of the Giza pyramid: rather than asking how?,
it is more fruitful to ask why? considering the resources/technology in manpower/hours such to construct.
It turns out the Giza pyramid utilized the same triangle as seen in the above π by way of Φ derivation:
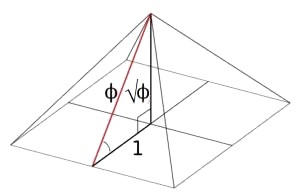
and thus encodes the relationship between space and time (ie. Φ and π²) as intrinsic to its own design/construction.
The axes of '4' act as radii moving from the center equidistant, thus find equality in one another
while producing 8 total sides (each face is two-sided), recalling √(-8+8√5)=π=4/√Φ.
The remaining '1' of √'5' (of which '4' composes the transcendental axes) is not unity,
but the immediate local 'state' (ie. 'orientation') of the displaced body as it concerns unity.
The 2x2 '4' axes is thus merely (though significantly) two pairs of null roots and operators
(+/-) whose own shared roots are both: real and imaginary, all of which discretely
concerns unity (or not) according to the particular discretion (or not) of the operator(s) in relation to '16'.
These are reflected in/as the four roots of f(x) = x⁴ - 16x² - 256 (as shown above) recalling x² - x = 1 as well as:
Recalling the first of the postulates:
The posited transcendental axes is a discretionary axis that can be seen asR/S System of Theory Postulates:
1. The universe is composed of one component, motion, existing in three dimensions, in discrete units, and with two reciprocal aspects, space and time.
universally bestowed, locally employed
according to the discretion of the operator,
as in: to be (+)... or not to be (-)... - that is the (real) discretion...
as well as the (imaginary) question (since all science is some faculty of inquiry).
However, because one axis affects the other, neither can be said to be a/the discretely real or discretely imaginary axis,
as the constituency of the entire '4' axes is itself 'transcendent' physically as well as 'real' metaphysically.
Thus f(x) = x⁴ - 16x² - 256 having two imaginary and real roots concerning unity seems to be whence
the natural discretionary limit begins/ends concerning what is real and what is imaginary.
If one were to theoretically "stand" in this 4x4 (16) grid and attempt to find the '1' that is unity,
they would find that it is not actually one particularly discrete unit therein, but rather contained in/as the constituency of the whole
and the same is (as necessitated to be) true for the posited transcendental axes of '4': though neither axis is discretely real/imaginary,
unity is the constituency of/as the whole of the axes, thus both physically transcendent while metaphysically real.
Another way of seeing this is by an inside-out approach, beginning with unity '1'
(as Mr. Larson did with his over-arching approach to RSoT)
and employing multiplicative expansion therefrom into 16:
1>2>4>8>16 wherein
1 is unity,
2 is unity and not (begets a binary polarity to/from concerning unity),
4 is the transcendental axes concerning unity (begets 2x2 binaries {all/not}{causation/cessation})
16 is discretely the particular collapsed 'state' and/or 'orientation' of the concerned body
To see how the axes meets/composes √5
(ie. a discretionary human being in space/time)
similarly working from the inside-out: (Φ) contains the axes as intrinsic to √5, with the additional 1
to concern unity (to/from) both internally and externally
(2(Φ)-1)² acknowledges both: birotation (2) and discretion concerning
{alpha/omega} by subtracting the discretion discarded (-1)
(A/5) couples the total energy of A via A/A(t/s) such to resolve at s²/t²
given s³/t→s²/t²→s/t³:t³/s→t²/s²→t/s³ concerns unity if/when 4²/4²
(the key being kinematic π is always bound to 4 about the golden root √Φ)
Therefor, √A (as ±A) intrinsically captures/employs the axis {alpha and omega},
capturing the discretion (or not) concerning unity, thus begetting {beg/end},
and is equal to its own particular s/t (dis)placement according to its own discretion
(that is: discretionary use of energy as t/s) and all relative motion is thereby discretely captured
and can thus be accounted for.
To close, with summary:
If we let *A be variable (+/-) discretion itself as 1/5The extent to which we have accomplished the purpose of our existence depends
on the nature of the structure that we have built, not on the amount of sunshine
during the progress of the work.
-Dewey B. Larson
(such to discretely both implicitly and explicitly +concern (or -not) unity = √1)
thus granting *A the transcendental 2x2 axes as 4/5
(thus completing the √5 of Φ)
({root}←{operator}←*axes*→{operator}→{root})
*A/5 expands:
1/5 ←←*A→→
5/5 {beg/end}←{alpha}←*A→{omega}→{end/beg}
_______________________________________________
thus:
√5 = 2x2 transcendental axes + 1x variable (+/-) discretion,
Φ = 16/π² captures all spacial (dis)placement(s) concerning unity,
π² = 16/Φ captures all temporal (dis)placement(s) concerning unity,
Φπ² = 16 thus wholly and discretely concerns unity
for both wholly and discretely containing unity
within itself.
1 = 16/Φπ² ∞ *u ∞ Φπ²/16 = 1