"Bless us, divine number, thou who generated gods and men! O holy, holy Tetractys, thou that containest the root and source of the eternally flowing creation! For the divine number begins with the profound,
pure unity until it comes to the holy four; then it begets the mother of all, the all-comprising, all-bounding, the first-born, the never-swerving, the never-tiring
holy ten, the keyholder of all."
"By that pure, holy, four lettered name on high,
nature's eternal fountain and supply,
the parent of all souls that living be,
by him, with faith find oath, I swear to thee."
Henosis
Henosis (Ancient Greek: ἕνωσις) is the classical Greek word for mystical "oneness", "union" or "unity." In Platonism, and especially Neoplatonism, the goal of henosis is union with what is fundamental in reality: the One (Τὸ Ἕν), the Source, or Monad.[1] The Neoplatonic concept has precedents in the Greek mystery religions[2] as well as parallels in Eastern philosophy.[3] It is further developed in the Corpus Hermeticum, in Christian theology, Alevism, soteriology and mysticism, and is an important factor in the historical development of monotheism during Late Antiquity.
Etymology
The term is relatively common in classical texts, and has the meaning of "union" or "unity".[note 1]
Process of unification
See also: Nepsis and Theoria
Henosis, or primordial unity, is rational and deterministic, emanating from indeterminism an uncaused cause. Each individual as a microcosm reflects the gradual ordering of the universe referred to as the macrocosm. In mimicking the demiurge (divine mind), one unites with The One or Monad. Thus the process of unification, of "The Being" and "The One," is called henosis, the culmination of which is deification.[citation needed]
Plotinus
Henosis for Plotinus (204/5–270 CE) was defined in his works as a reversing of the ontological process of consciousness via meditation (in the Western mind to uncontemplate) toward no thought (nous or demiurge) and no division (dyad) within the individual (being). As is specified in the writings of Plotinus on Henology,[note 2] one can reach a tabula rasa, a blank state where the individual may grasp or merge with The One. This absolute simplicity means that the nous or the person is then dissolved, completely absorbed back into the Monad.
Within the Enneads of Plotinus the Monad can be referred to as the Good above the demiurge.[5][6] The Monad or dunamis (force) is of one singular expression (the will or the one is the good), all is contained in the Monad and the Monad is all (pantheism). All division is reconciled in the one, the final stage before reaching singularity, what is called duality (dyad) is completely reconciled in the Monad, Source or One (see monism).
As the one, source or substance of all things the Monad is all encompassing. As infinite and indeterminate all is reconciled in the dunamis or one.
It is the demiurge or second emanation that is the nous in Plotinus. It is the demiurge (creator, action, energy) or nous that "perceives" and therefore causes the force (potential or One) to manifest as energy, or the dyadcalled the material world. Nous as being, being and perception (intellect) manifest what is called soul (World Soul).[7]
Plotinus words his teachings to reconcile not only Plato with Aristotle but also various World religions that he had personal contact with during his various travels. Plotinus' works have an ascetic character in that they reject matter as an illusion (non-existent). Matter was strictly treated as immanent, with matter as essential to its being, having no true or transcendential character or essence, substance or ousia. This approach is called philosophical Idealism.
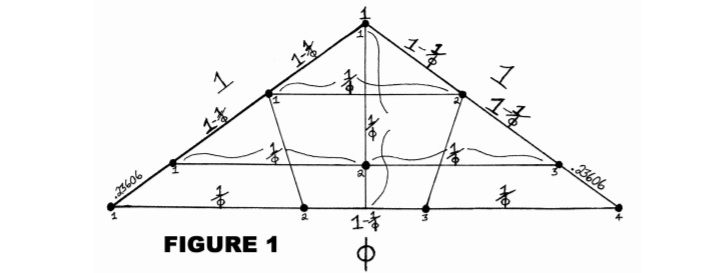
 Pythagorean symbol
Pythagorean symbol
The first four numbers symbolize the musica universalis and the Cosmos as:
(1) Unity (Monad)
(2) Dyad – Power – Limit/Unlimited (peras/apeiron)
(3) Harmony (Triad)
(4) Kosmos (Tetrad).[4]
The four rows add up to ten, which was unity of a higher order (The Dekad).
The Tetractys symbolizes the four classical elements—fire, air, water, and earth.
The Tetractys represented the organization of space:
the first row represented zero dimensions (a point)
the second row represented one dimension (a line of two points)
the third row represented two dimensions (a plane defined by a triangle of three points)
the fourth row represented three dimensions (a tetrahedron defined by four points)
A prayer of the Pythagoreans shows the importance of the Tetractys (sometimes called the "Mystic Tetrad"), as the prayer was addressed to it. (see top along with the Pythagorean oath)
https://en.wikipedia.org/wiki/Tetractys
Photon model as a Quaternion
viewtopic.php?f=14&t=231&hilit=scale
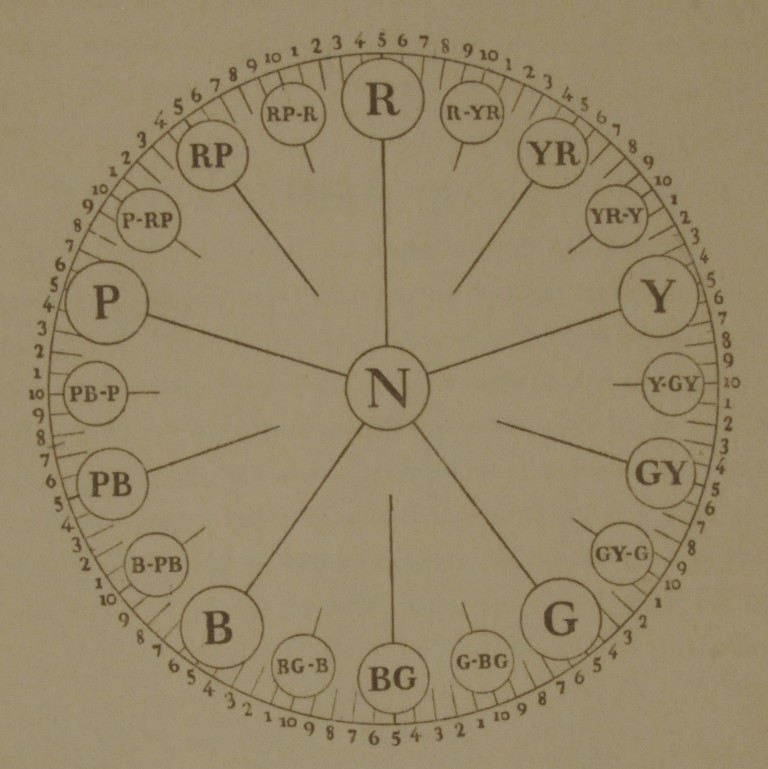
The Munsell Book of Color 1929: The Color Sphere
 Photon 2.0
viewtopic.php?f=7&t=597&hilit=scale
Photon 2.0
viewtopic.php?f=7&t=597&hilit=scale
bperet wrote:
Djchrismac wrote: ↑
Mon Sep 24, 2018 11:25 pm
His presentation is also relevant as he mentions Edmond Halley, father of the Hollow Earth Theory, who studied the magnetic field of the earth and imagined a magnetized interior and concentric spheres rotating at different speeds and forcing the magnetic field to move.
Halley's research was, as they say, "right pew, wrong church." He recognized that rotation and magnetism was involved, but without the RS, never put them together as "magnetic rotation" -- speed ranges, as documented in the --daniel paper, "The Annunaki Strike Back."
After all,
matter is just a temporal/magnetic rotation, so different speed ranges would LOOK like a series of discrete, concentric spheres in the Earth from a non-RS perspective.
Frequency as angular recursion
bperet wrote: ↑Sat Jan 05, 2019 11:18 am
Wow, it is hard to believe that I started this idea of a photon as a quaternion 7 years ago (first post:
Photon model as a quaternion, posted: 15-Feb-2012) and it has taken all that time and dozens of dead-ends to get where it is now. It is interesting to review how I get from one idea to another.
I have been looking for a way to convert the color quaternion to a conventional representation of frequency and ended up building a spreadsheet of the known frequency bands. One of the things that has always bothered me was the sheer number of "natural units" (Larson's "direction reversals") that must be packed together to get to the extremely low frequency band (ELF), the bottom of which--the longest wavelength--being some 2,194,763,294,778,660 "units" -- that's TWO QUADRILLION UNITS. Given that all the other displacements in the Reciprocal System don't get higher than ±16, I cannot see how this can be a viable structure, or a "natural consequence."
Last night I realized that the frequency spectrum is a logarithmic scale (base 10 log) and the log of this ELF frequency is only about 15. Now THAT makes more sense... then I realized that, as an angular velocity,
frequency is a recursion. What I mean by that is that angular velocity, like speeds in the time region, is a growth measure--layers of skin on an onion, and only the
outer skin is the one that matters for interaction.
We see this structure already in Larson's atomic model, as well as conventional science. Take, for example, gold (AU), atomic number 79. With displacements of 4-4-(7), it
does not have 79 units of anything, because we don't count the inner layers (4-3, 3-3, 3-2, 2-2, 2-1) unless we want to get the atomic number. Conventional science does the same, by references to the prior noble gas: [Xe] 6s
1 4f
14 5d
10--it does not include all the inner electron orbitals.
The center of this "
onion" appears to be on the green/magenta rotation, at 12 natural units. Visible light runs from 8 (410nm) to 16 natural units of space (729 nm), an
octave. Octaves are common in Nature, so this makes sense (conventional spectrum is based on powers of the meter).
The next layer out runs from 4 (UV-A, 364 nm) to 32 (IR-A, 1458 nm) natural units. Now this seems like a big spread--but we did not remove the visible part from 8-16 units, upon which it is built.

Angular-Recursion.png
As a consequence of this recursion, the "A" band is split into two halves, UV-A (ultraviolet) and IR-A (infrared),
which is observed. The next layer is the UV-B:IR-B, then UV-C:IR-C.
What is not accounted for in the conventional frequency model is the reciprocal relation. We have the spatial displacements well documented (from red down to ELF), because the frequency distribution is exponential--the further you go from red, the larger the spatial gap (wavelength).
However, in the opposite direction, all we have is blue, UV, EUV (extreme UV), SX (soft X-rays), HX (hard X-rays) and gamma rays. Space seems to have been "compressed out"... because on this side, it isn't a
wavelength, but a
waveduration... the displacement is in time and "more time = less space." If one were to look from the temporal aspect, then we'd see dozens of bands, rather than just four of them.
This recursion model of the frequency spectrum also parallels
Nehru's concept of "electric folds" that he once presented to explain atomic orbitals. It also makes the photon behave in the same manner as other rotating systems, both magnetic and electric. However, it also proves that Larson's model of the "direction reversal" is wrong (only applicable to low displacements in the visible light region).
Goethe on Color
http://forum.antiquatis.org/viewtopic.php?f=20&t=1783
LoneBear wrote: ↑Tue Feb 09, 2016 11:20 am
Something I noticed many years ago, was that the EM spectrum (Newton version) came in chunks of 256 natural units of space (2^
8), and that the colors of the rainbow hit very nearly on integer multiples of the unit of space, as wavelengths, between 8 and 15 natural units (1 octave, 16 starts iR). This
chart is available on the RS2 site:

RS-visible-spectrum.gif
Couple of other things I noticed between light and music:
Light is continuous in the time of the reference system (on), whereas music is discontinuous in the time of the reference system (notes). For example, during a concert, we hear a bunch of different frequency notes, whereas the lights over the musicians are constantly on at the same frequency.
Also, light is discontinuous in the space of the reference system--made of bundles of photons, whereas music is continuous--a song filling a room.
This indicates that light is a time region (material) phenomenon, whereas music is more "space region" (cosmic). The body is made of atoms displaced in the time region; the soul's atomic structure is in the space region. Therefore, light affects the body and music affects the soul. (Using visible light; the inverse may apply to the X-ray/gamma ray side.)
Going back to the demiurge:
The Enochian Apocalypse
https://www.bibliotecapleyades.net/bb/bluebook418.htm
It has always been generally assumed that the apocalypse is in the hands of the angels of wrath, to be visited upon the world at the pleasure of God, at a moment preordained from the beginning of creation. In the veiled teachings of the Enochian angels this is not true. The gates of the Watchtowers can only be unlocked from the inside. The angels of wrath cannot initiate the apocalypse even if they wish to do so. This is suggested by an exchange between Dee and the angel Ave:
Dee - As for the form of our Petition or Invitation of the good Angels, what sort should it be of?
Ave - A short and brief speech.
Dee - We beseech you to give us an example: we would have a confidence, it should be of more effect.
Ave - I may not do so.
Kelley - And why?
Ave - Invocation proceedeth of the good will of man, and of the heat and fervency of the spirit: And therefore is prayer of such effect with God.
Dee - We beseech you, shall we use one form to all?
Ave - Every one, after a divers form.
Dee - If the minde do dictate or prompt a divers form, you mean.
Ave - I know not: for I dwell not in the soul of man. (8)
Spiritual beings must be evoked into our reality by human beings. We must open the gates and admit the servants of
Coronzon ourselves. Evocation and invocation are not a part of the business of angels, but of humans. That is why the angels needed to go through the elaborate ruse of conveying the system of Enochian magic, with the Keys and the Great Table of the Watchtowers, to Dee. If the apocalypse is to take place, and if it is necessary for human beings to open the gates of the Watchtowers before it can take place, the angels first had to instruct a man in the correct method for opening the gates.
It is evident that Dee was to be restrained from opening the gates of the Watchtowers until it pleased the angels. The angel Gabriel, who purports to be speaking with the authority of God, tells him:
"I have chosen you, to enter into my barns: And have commanded you to open the Corn, that the scattered may appear, and that which remaineth in the sheaf may stand. And have entered into the first, and so into the seventh. And have delivered unto you the Testimony of my spirit to come.
"For, my Barn hath been long without Threshers. And I have kept my flayles for a long time hid in unknown places: Which flayle is the Doctrine that I deliver unto you: Which is the Instrument of thrashing, wherewith you shall beat the shears, that the Corn which is scattered, and the rest may be all one.
"(But a word in the mean season.)
"If I be Master of the Barn, owner of the Corn, and deliverer of my flayle: If all be mine (And unto you, there is nothing: for you are hirelings, whose reward is in heaven.)
"Then see, that you neither thresh, nor unbinde, until I bid you, let it be sufficient unto you: that you know my house, that you know the labour I will put you to: That I favour you so much as to entertain you the labourers within my Barn: For within it thresheth none without my consent."(9)
Macrobes, Silicon, Serpents & John Dee
https://forum.antiquatis.org/viewtopic. ... it=holy+10
"Serve us, and we shall show you where our "flayles" are hidden (technology). It seems with must disgust these entities maintained this contact, but remember. The original alien masters were HIGHLY intelligent, had vast working knowledge of space/time/planes of consciousness and manipulation of matter. They could also probably, very easily maintain consciousness after physical death"
https://en.wikipedia.org/wiki/Choronzon
Choronzon /ˌkoʊˌroʊnˈzoʊn/
is a demon or devil that originated in writing with the 16th-century occultists Edward Kelley and John Dee within the latter's occult system of Enochian magic. In the 20th century he became an important element within the mystical system of Thelema, founded by Aleister Crowley, where he is the "
dweller in the abyss",[1][2] believed to be
the last great obstacle between the adept and enlightenment.
Thelema

Does
Coronzon remind you of anything? Let us examine this further:
https://www.bibliotecapleyades.net/bb/bluebook418.htm
A Mental Armageddon
Fundamentalist Christians commonly believe that the end of the world will be a completely physical event and will be sparked by some horrifying material agent -- global thermonuclear war, or the impact of a large asteroid, or a deadly plague.
This supposition is natural in view of the concrete imagery of the book of Revelation. It is in keeping with the materialistic world view of modern society. But nobody stops to consider that this destruction is described by angels, or that angels are spiritual, not physical, beings.
In my opinion the apocalypse prepared by the Enochian angels must be primarily an internal, spiritual event, and only in a secondary way an external, physical catastrophe. The gates of the Watchtowers that stand guard at the four corners of our dimension of reality are mental constructions. When they are opened, they will admit the demons of Coronzon, not into the physical world, but into our subconscious minds.
Spirits are mental, not material. They dwell in the depths of mind and communicate with us through our dreams, unconscious impulses, and more rarely in waking visions. They affect our feelings and our thoughts beneath the level of our conscious awareness. Sometimes they are able to control our actions, either partially, as in the case of irrational and obsessive behavior patterns, or completely, as in the case of full possession. Through us, and only through us, are they able to influence physical things.
The Enochian communications teach not only that humanity itself must initiate the apocalypse through the magical formula delivered to Dee and Kelly, but that humans must be the physical agents that bring about the plagues, wars, and famines described with such chilling eloquence in the vision of St. John. It is we who will let the demons of Coronzon into our minds by means of a specific ritual working. They will not find a welcome place there all at once, but will worm their way into our subconscious and make their homes there slowly over time. In the minds of individuals that resist this invasion they will find it difficult to gain a foothold, but in the more pliable minds of those who welcome their influence they will establish themselves readily.
Once the demons have taken up residence, we will be powerless to prevent them from turning our thoughts and actions toward chaotic and destructive ends. These apocalyptic spirits will set person against person and nation against nation, gradually increasing the madness and chaos in human society until at last the full horror of Revelation has been realized upon the stage of the world. The corruption of human thoughts and feelings may require generations to bring to full fruition. Only after the wasting and burning of souls is well advanced will the full horror of the apocalypse achieve its final fulfillment in the material realm.
Let us suppose for the sake of argument that the signal for the initiation of this psychic invasion occurred in 1904 when Crowley received the Book of the Law, as he himself believed. Crowley’s Enochian evocations of 1909 then pried the doors of the Watchtowers open a crack enough to allow a foul wind to blow through the common mind of the human race. This would explain the senseless slaughter of the First World War and the unspeakable horror of the Nazi Holocaust during the Second World War. It would explain the decline of organized religions and why the soulless cult of science has gained supremacy. It would explain the moral and ethical bankruptcy of modern times and the increase in senseless violence.
We may not have long to wait before the individual known in the vision of St. John as the Antichrist, the one foretold in Crowley’s Book of the Law to follow after the Beast, will succeed in completing the Apocalypse Working. Then the gates of the Watchtowers will truly gape wide, and the children of Coronzon will sweep into our minds as crowned conquerors. If this chilling scenario ever comes to pass, the wars of the twentieth century will seem bucolic to those who survive the slaughter.
Those in control continue to dabble with dark forces, tread carefully my friends, apologies if this post seems a bit of a tangent but I am sure more will be revealed in due course.
Cheers.
Chris