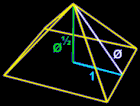
This thread culminated into the derivation of a more precise calculation of π as shown here:
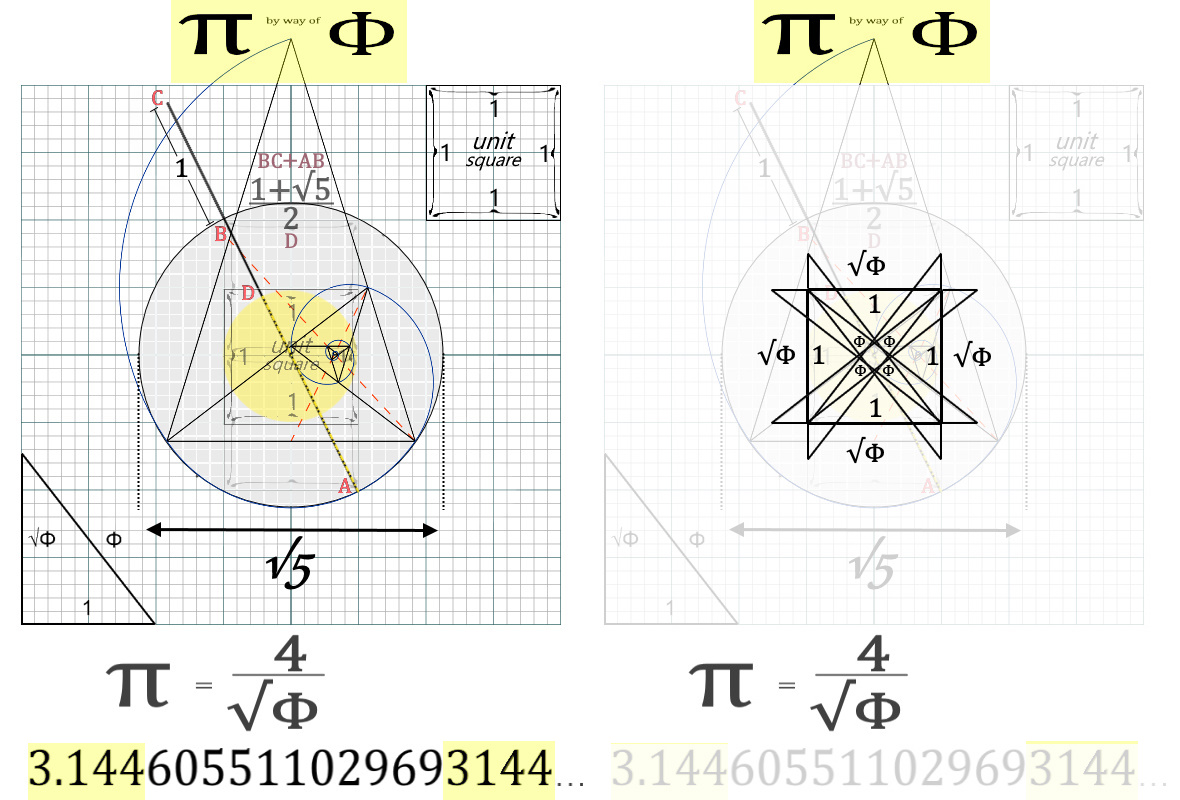
and elaborated on page 3.Beginning with a circle whose diameter is √5,
place two unit squares inside of the circle side-by-side
(either horizontally or vertically, the latter is shown)
and find √5 as any diagonal between two opposite corners (AB shown).
Note: this diagonal is equal to the diameter of the circle as √5.
Add 1 unit distance (BC shown) to this diagonal and find the midpoint (D shown)
such to satisfy (√5+1)/2 as (AB+BC)/D wherein D effectively halves AC.
By rotating the √5 diagonal about the origin of the circle we began with,
the midpoint (D) incessantly coincides with the circle whose diameter is 2r = 1
and "kisses" the unit square four times equidistantly, thus a more precise π
can be measured directly by way of Φ expressed as a ratio of Φ.
This ratio is 4/√Φ and/or (8√5-8)1/2
Concerning:
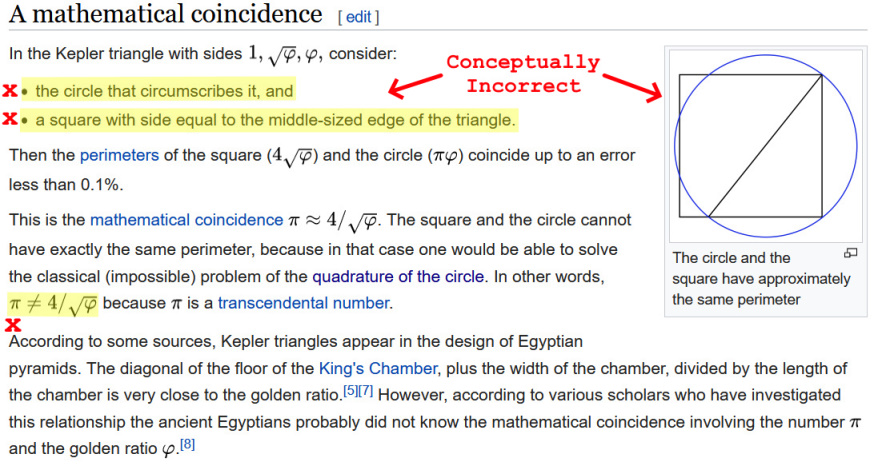
https://en.wikipedia.org/wiki/Kepler_triangle
I am unsure as to the motive for the above, but the construction of the geometry
is conceptually unsound: concerning the same Kepler triangle, a circle that circumscribes it
completely ignores the imperative need for the diameter of the circle to be √5, the same to which
the Kepler triangle must apply. If the circle is not √5, there is no valid coupling and π remains 'transcendental'
however if coupled to the √5 diameter circle (as shown), the coupled relation permits a geometry
whose co-operation between Φ and π are respectively reflected in the following:
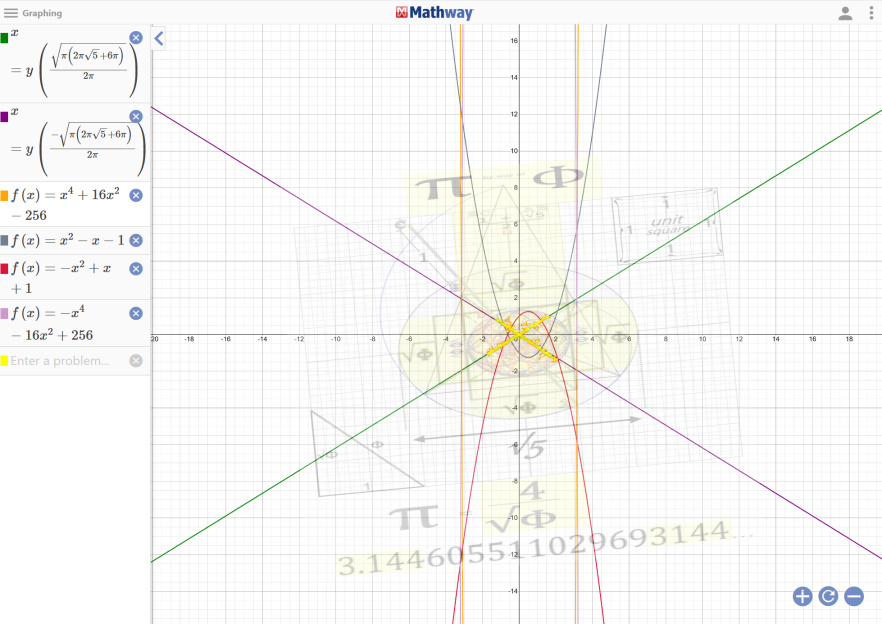
Φ solves for
f(x) = x² - x - 1
π as 4/√Φ solves for
f(x)=x4 + 16x2 - 256
thus
16=Φπ²
and General Relativity states:
e=MC²
thus must concern the herein derived:
1=Φπ²/16
The former f(x) graphed with an overlay of the same geometry:
__________________________________________________________________________

This is important because it confirms the bi-rotation model (mandated by the geometry as intrinsic)
and implies a bi-orientation compliment, the properties of which can be derived inductively -
the implications of which amounts to the capacity to calculate universal roots using universal geometries
that satisfy cubed proportionality (as time and space reciprocally do) viz. (s³/t ∞ t³/s).