Hi Doug, I am not a "follower" of anyone, just my own internal logic and gut feelings. Bruce did a brilliant job of describing Larson's RS and RS2, as does Gopi, in ways that I can understand that don't involve a lot of equations and mathematics.
I have read through your posts on here and also your website at
http://www.lrcphysics.com/.
This post in particular sums things up for me -
http://www.lrcphysics.com/general-discu ... st/2013618
I can see why Mildred never returned as I too cannot follow your explanation of you theory.
On the page above you have written:
Ok, the first thing to understand in Larson's new system, is that it is a system of physical theory. Newton's system of physical theory is used to explain the behavior of matter, but not its origin.
Space and time in Newton's system contains matter and his system is used to explain the interactions between particles of matter, from planets to electrons. Larson's system on the other hand, begins with nothing but motion.
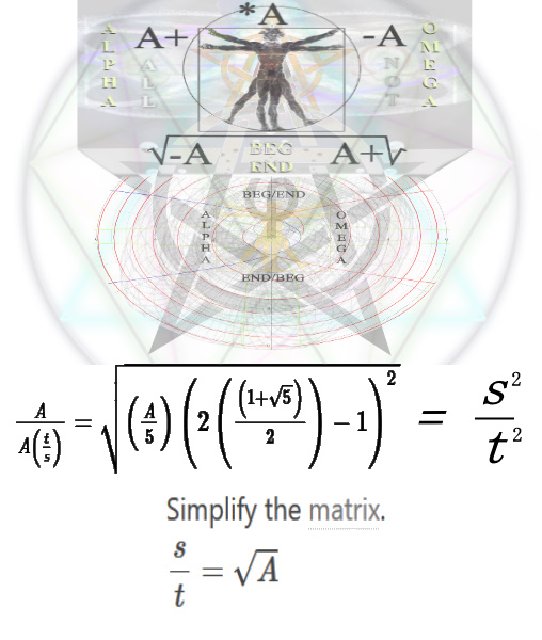
Consequently, the motion cannot be the movement of anything. It is simply a universal increase of space and time, the very definition of motion. We can understand it in numerical terms as the eternal increase of two numbers, s and t, one the inverse of the other, s/t.
We can understand still more, if we give the numbers s and t geometrical meaning, by assigning dimensions to them, s^3/t^3 for instance. Thus, we can conceive of a uniform eternal progression,
s^3/t^3 = 1/1, 2/2, 3/3, ...n/n,
as simply an eternally increasing number. In order for something to come out of this perfect uniformity, however, there must be some deviation from unity. The only way that this can occur is if there is a periodic reversal in the denominator or numerator of the number,
s^3/t^3 = 1/1, 2/2, 3/3, 2/4, 3/5, 2/6, 3/7, 2/8, ....
Here, we see the reversals in the numerator, meaning that the space aspect of the motion at this "location" in the progression is not increasing, but oscillating, while the reciprocal, or time, aspect continues to progress normally.
In a sense, the spatial non-progression at this point in the progression creates a stationary entity that is progressing in time only. If the periodic reversals had commenced in the denominator of the number, or the time aspect of the motion, the oscillating entity would have been stationary in time and progressing in space.
As more and more entities of these kinds are created, the distance between them, whether space or time is determined by the space/time distance between the instances occurring in the uniform progression, the amount of progression between the instances of the commencement of periodic reversals.
Thus, in effect, coordinate space and coordinate time are created by the initiation of periodic reversals in one or the other aspects of the uniform progression. How, when or why this happens is impossible to say, but the system requires it.
Now, in Larson's development of the RST, the periodic reversals occur first in one of the three dimensions, while the remaining two dimensions continue progressing normally. We have taken another route of development at the LRC, which assumes that the reversals occur in all three dimensions simultaneously.
Regardless, however, the result is the same in both cases, as far as the emergence of coordinate space and coordinate time is concerned. The coordinate locations in space and time are created by the effective cessation of progression in one aspect or another of the unit progression at a given point in the progression. Once these positions are occupied by non-progressing, oscillating entities, the postulates of geometry can be satisfied for the set of them.
Of course, once these coordinate positions are occupied by oscillating entities, there is nothing preventing them from changing these coordinate positions, if they are acted upon in some way consistent with their properties.
It is the logical development of their properties, consistent with observed properties of matter, that we are seeking to accomplish at the LRC.
I hope this helps. More later.
November 29, 2012 | Doug
Now that we have established non-progressing, oscillating, entities of scalar motion in coordinate space (time) simply by introducing periodic reversals into the uniform progression, we need to consider how they behave and interact and how this behavior and interaction changes as they combine into more complex entities of scalar motion.
Before delving into this fascinating subject, however, we should understand that since the non-progressing oscillation of the entities is three-dimensional, in the case of the LRC development of the consequences of the system, and their non-oscillating, reciprocal, aspect is three-dimensional, the coordinate space (time) between them constitutes the space (time) aspect of the scalar motion that has occurred between their instantiation, at the onset of the periodic reversals:
A -------> B -------> C
However, since the uniform progression is three-dimensional, this is not as straight forward as a linear progression, A->B->C, would be. Consider the progression before point A for instance, the progression at point A-1, we can say. The 3D scalar increase from A-1 to A creates a one-unit ball, and point A-1 therefore becomes a spherical surface at “point” A in the progression. The question is, therefore, where on this surface is point A?
Clearly, any point on the sphere qualifies as the next point in the progression! Consequently, since the instantiation of A by the reversal process must collapse the previous expansion back to the previous point A-1, the entire surface must collapse back to point A-1. Thus, the 3D oscillation is a one-to-many, many-to-one periodicity, while the non-oscillating 3D progression is a continuous many-to-many process.
This development has many implications, but the most important to understand at this stage is that since the continuous time (space) expansion of the entity is the inverse of its oscillating space (time) aspect, its effect on the behavior of the entity is inverse; that is, its 3D increase of time is equivalent to a 3D decrease of space.
We can view this as the effect of the oscillation, which, in effect, prevents the entity’s space aspect from progressing and thereby creates an imbalance in its space/time progression, causing it to continuously increase in time only, which is equivalent to a decrease in space, since time is the inverse of space.
The result is what we call gravity: Oscillating entities of scalar motion are, in effect, consumers of space, causing them to appear to attract one another at all times.
November 30, 2012 | Doug
Are you saying that space and time are both expanding in a scalar motion, in the same direction, yet gravity is caused when space decides to oscillate and time doesn't?
What initiates periodic reversals in one or the other aspects of the uniform progression?
What if your assumption below, and several others you admit to, are incorrect assumptions? Would it not be better to eliminate your assumptions by referring to funamental postulates in order to remove any doubt and confusion and settle on a definitive answer?
Now, in Larson's development of the RST, the periodic reversals occur first in one of the three dimensions, while the remaining two dimensions continue progressing normally. We have taken another route of development at the LRC, which assumes that the reversals occur in all three dimensions simultaneously.
Regardless, however, the result is the same in both cases, as far as the emergence of coordinate space and coordinate time is concerned. The coordinate locations in space and time are created by the effective cessation of progression in one aspect or another of the unit progression at a given point in the progression. Once these positions are occupied by non-progressing, oscillating entities, the postulates of geometry can be satisfied for the set of them.
November 29, 2012 | Doug
What is it that stops the natural progression of the reference system in a universe of motion, this oscillation you speak of? Could you please give a detailed description of how gravity works in your version of the RSoT?
Could you also explain coronal holes in the sun to me using your theory? I understand this well in RS2 terms so it might be a good place to provide more detail after you explain gravity to me in LRC terms. Thanks.
The following page is another attempt to explain the theory:
http://www.lrcphysics.com/general-discu ... st/1560625
Your explanation does not help i'm afraid, it only confuses further:
This is the most difficult concept for beginners. Nothing has to move, since the definition of motion is a change of space and time. We are used to a change in an object's location to indicate the change of space, in the equation of motion. However, we are conscious of a change in time without requiring something to move.
Think of a space clock marking the increase of space, as a time clock marks the increase of time.We refer to this as the space/time progression: One unit of space increase for each unit of time increase.
As for the definition of space and time, the only definition we have is that they are the reciprocal aspects of motion. If this seems to beg the question, it does. I don't know how to get around that. One of the most fundamental facts of nature is that if two things exist, one greater than the other, then we can be sure that there is a third, greater than them both.
The good news is that the concept of increasing space and an increasing reciprocal of time, is perfectly reflected in the system of numbers and the structure of geometry.
When we begin with space and time, we begin with magnitude, dimension and "direction," where "direction" are the two "directions" inherent in a given dimension. As these dimensions are compounded into one three-dimensional construct, the two "directions" grow to a maximum of eight "dimensions" that enable us to define an infinitude of directions in terms of them.
I hope this helps.
Update: The word "dimensions" in the last sentence, should read "directions" instead. The mainstream mathematicians confuse "directions" with "dimensions" and this may explain why I used the wrong word.
July 29, 2011 | Doug
The part in bold baffles me and you sound confused at your own explanation.
What is this third fundamental factor of nature that is bigger than space and time? Is motion not your fundamental factor with space and time being a reciprocal relationship of this? Is your frame of reference as an observer only in space/time and you cannot make the jump over to time/space to view the unverse from that perspective?
How does the LRC explain the inverse/temporal region, where space is in one dimesion and time is in 3 dimensions, a landscape of time? I have not seen an explanation of this.
How does LRC explain faster than light motion? I have not seen this mentioned anywhere.
Do you agree with the fundamental postulates of RS2?
1. The universe is composed of one component, motion, existing in three dimensions, in discrete units, and with two reciprocal aspects, space and time.
2. The universe conforms to the relations of ordinary mathematics, its primary magnitudes are absolute, and its geometry is Projective*.
* an RS2 update from Larson's original "its geometry is Euclidean"
What are the fundamental postulates of LRC physics?