Sadly, nothing ever came of it. However, with the LRC's RST-based theory (RSt), which has taken us down a different path of theoretical development, compared to Larson's RSt, it now may be possible to devise the coveted experiment. The reason for the new optimism is the fact that we now have an RSt model of the observed elementary particles and of the atomic spectra groups, as well as a new understanding of the periodic table of the elements, together with a new mathematical approach to quantify it all.
All this brings with it a much simplified model of the atom, as a combination of space and time scalar motions, wherein we can explore physical phenomena, as relations between motion combinations. A good place to start might be with particle interactions. Right now the LST community is spending beaucoup bucks studying neutrinos and cosmic rays and dark matter.
One of the investigations is a search for "sterile" neutrinos, meaning inert neutrinos that haven't been detected. The reason they are thinking that they might exist, though, is due to what they see as a lack of symmetry in the interactions of particle physics. They love symmetry almost as much as we do, because of its links to laws of conservation.
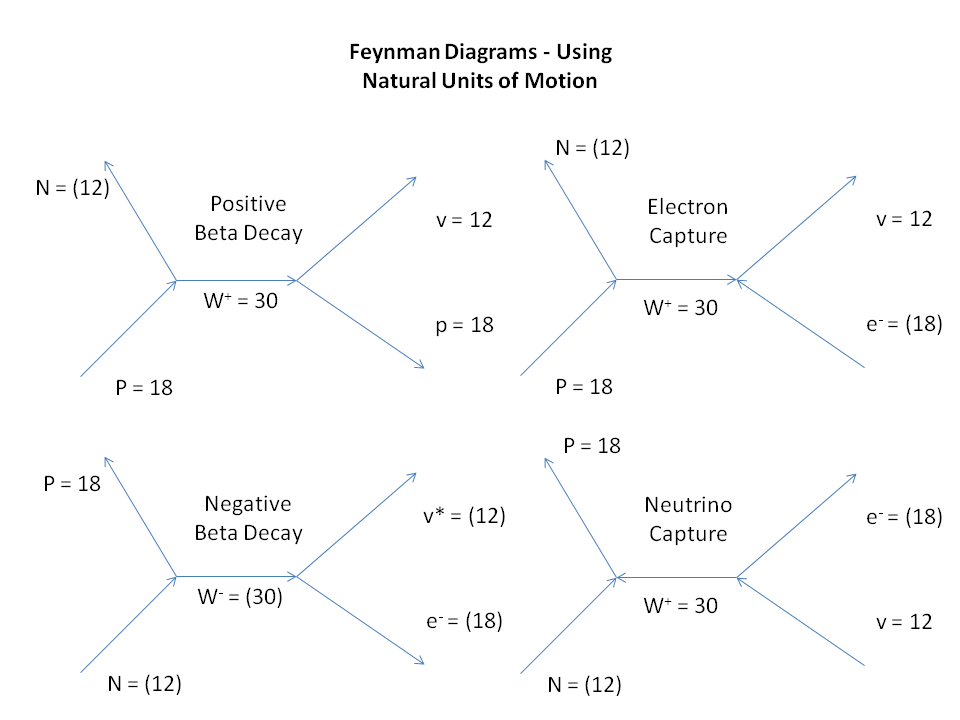
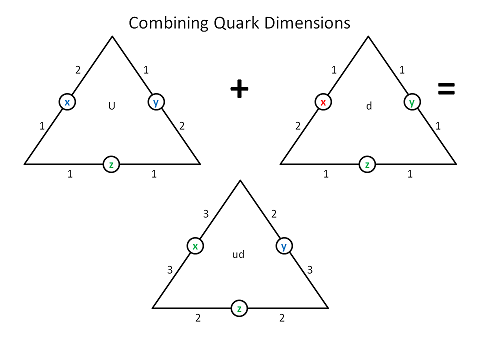
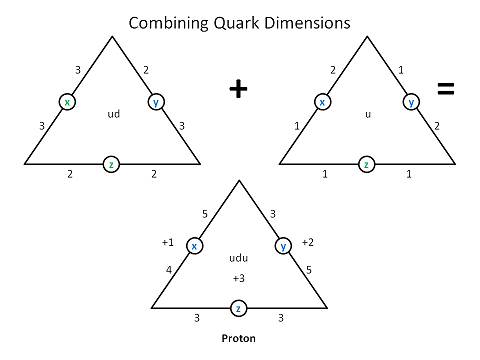
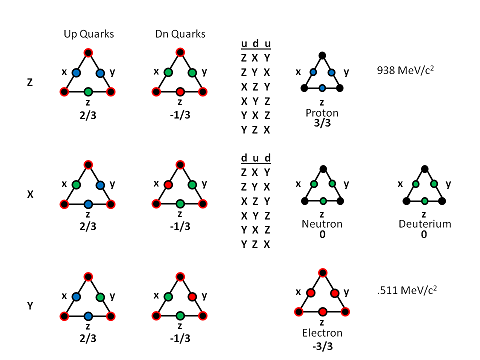
In this case, the lack of symmetry is found in the fact that positive and negative beta decay happens with the production of right-chiral positrons and left-chiral electrons, respectively, along with their associated neutrinos, but not vice-versa. No such decay takes place that produces right-chiral electrons or left-chiral positrons. These four particles can be seen clearly in our model, which was originally based on the LST's Bilson-Thompson braid model, and we've followed it ever since, deriving the natural units of motion (num), for each particle, as shown in the table of the following graphic:
However, it's not that easy to see in the LST language. Several mistakes have been made in various presentations of the topic that tend to confuse people. For instance, here is one presentation with great animations, but they got the charge signs wrong on the positrons:
https://www.youtube.com/watch?v=0mXW1zPlxEE&t=309s
So, left-chiral neutrinos are produced with right-chiral positrons, in positive beta decay, and right-chiral anti-neutrinos are produced with left-chiral electrons, in negative beta decay, and all of this has to do with quantum spin, the nature of which the LST has no clue, while we can explain it easily.
I'll have more to say about this, of course, but I also want to reference the MiniBoone investigation mentioned in the above video, where they want to find sterile neutrinos to help explain how their heavier muon neutrinos quickly transform into lighter electron neutrinos, if indeed they do so.
Here is a new slide presentation on several experiments along this line:
https://theory.fnal.gov/wp-content/uplo ... eminar.pdf
It's very technical and obtuse for non-specialists, but it conveys a sense of the lengths they're willing to go to, in order to explain the observed anomalies, including the consideration of extra dimensions!
Given our much simpler system of theory, we would immediately conclude that there can be no other neutrinos, since the neutrinos (in each family, of course) are the neutral, or foundational, particles of the material and cosmic sectors of our theoretical universe. That is the reason they occupy the center position in the graph, between the three s/t (velocity) and the three t/s (energy) particles. They are neutral, or balanced entities, we might say, just as unit progression (s/t (t/s) = 1/1) is unit speed (energy), in the triality of the RST. The LST's lack of recognition of this fact, blinds them to the true nature of the particles and the beauty of their inherent symmetry.
It turns out, though, that the Bilson-Thompson braid model, which we have based our particle schematic upon for years now, because it is well-known and accepted by the LST community, doesn't follow the reciprocity of the LRC's RSt, as it has developed over the intervening years. We've ignored this annoying fact, as we have gone along, because we could still use it to great advantage and we didn't want to run the risk of violating some well-known, but obscure, physical principle.
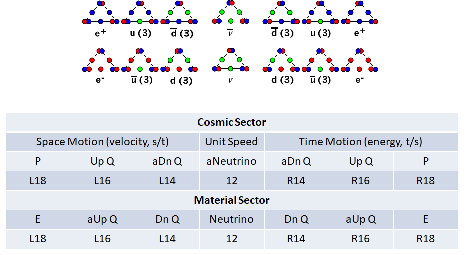
However, in the study of the neutrinos and in the context of the search for a "crucial" experiment, the need to rectify this situation has become apparent. Therefore, the following graphic shows the theoretically correct, or at least a more consistent way to order the particles in our theory:
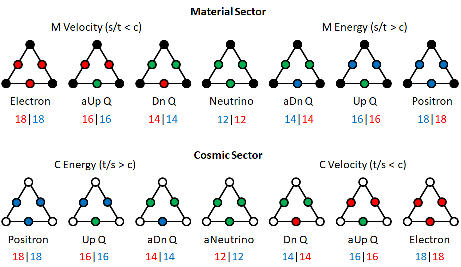
In the above graphic, the color of the vertices has been changed to black and white, in order to convey the reciprocal nature of the two sets of particles more clearly. The chirality is obvious, given the left and right side of the middle position of the two neutrinos. The colors of the less than 'c' speed S|T units is red, while it is blue for the greater than 'c' speed T|S units, for the material sector particles. Of course, this color scheme is reversed for the cosmic sector set of particles. It's easy to see that the cosmic sector set is just the material sector set, rotated horizontally around the neutrino.
This makes the cosmic sector neutrino (with the white vertices) the anti-neutrino, and no other possibility exists. In other words, the anti-neutrino is the reciprocal of the neutrino, which is why its spin is also opposite. The chirality of the neutrinos can't exist in this model, any more than it exists for two, opposite, sides of a coin, but more on this later.
What this new, reciprocal, arrangement of the particles gives us is the ability to investigate the particle interactions in a more straightforward manner. In fact, in the next post, we'll see how to do a version of Feynman diagrams, in terms of the interacting particles' num value.