Meeting a Terrific Challenge

[dbundy]

Using the new approach to our atomic model, where we increase the numbers of the up and down quarks in one tetrahedron, instead of trying to fit multi-tetrahedron together, as demonstrated in the previous post, we can use the scalar equations to calculate the combinations of scalar motion, belonging to a given element.

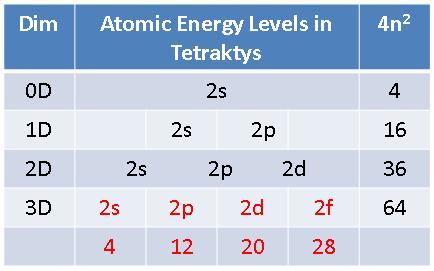
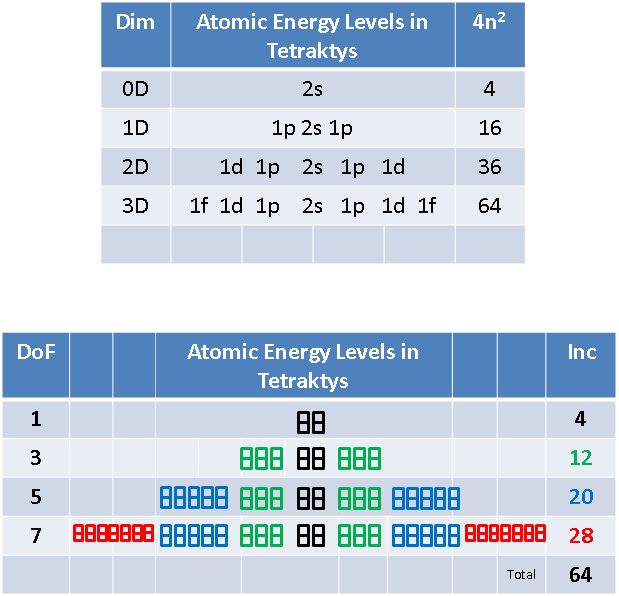
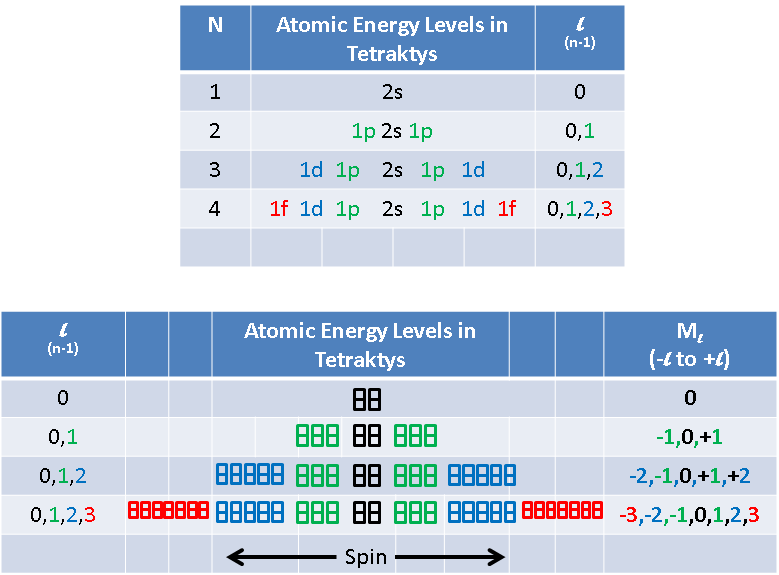
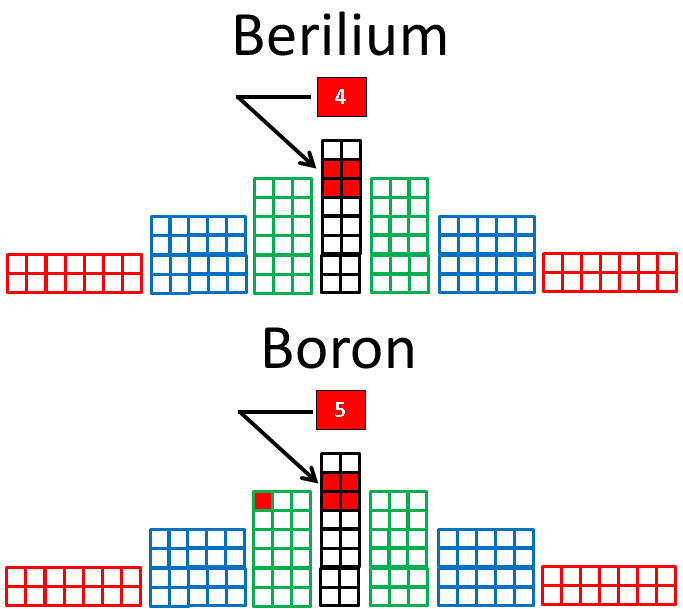
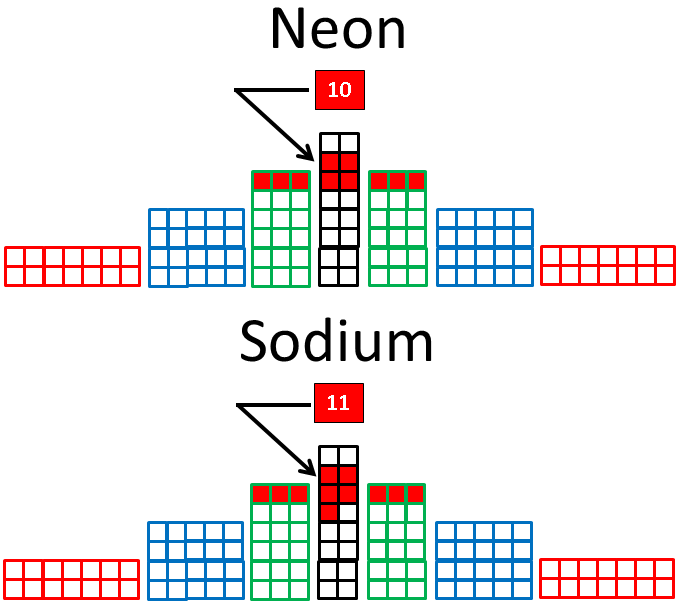
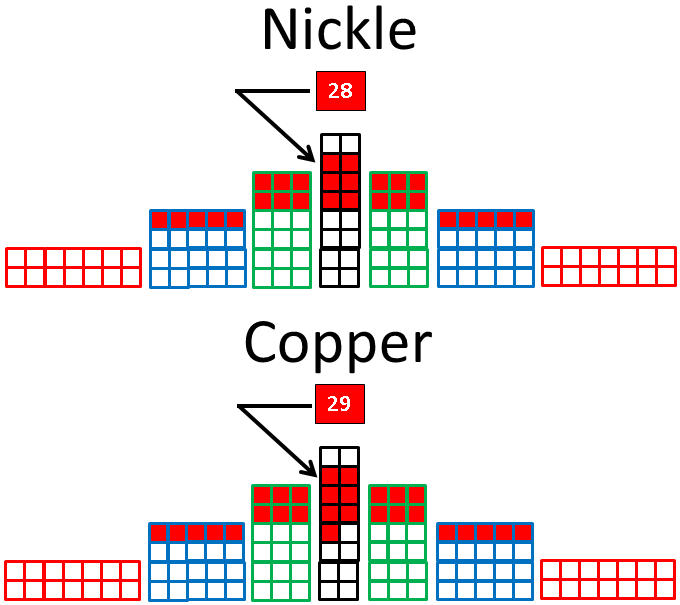
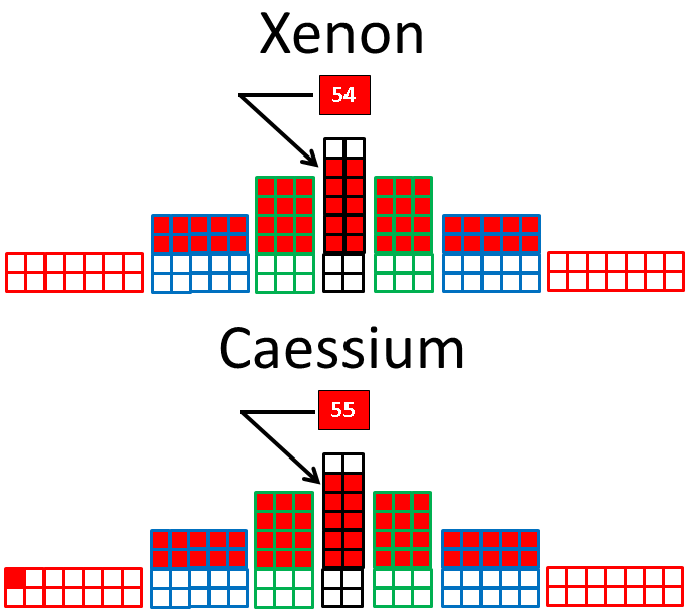
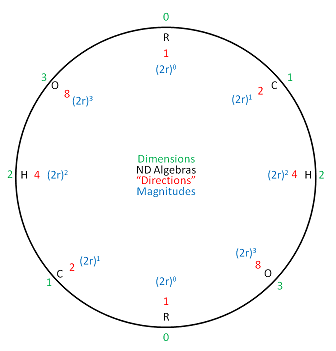
Also, instead of trying to cope with the drawing of atomic elements in the circles of the wheel of motion, we can transform the wheel back into a periodic table, as follows:



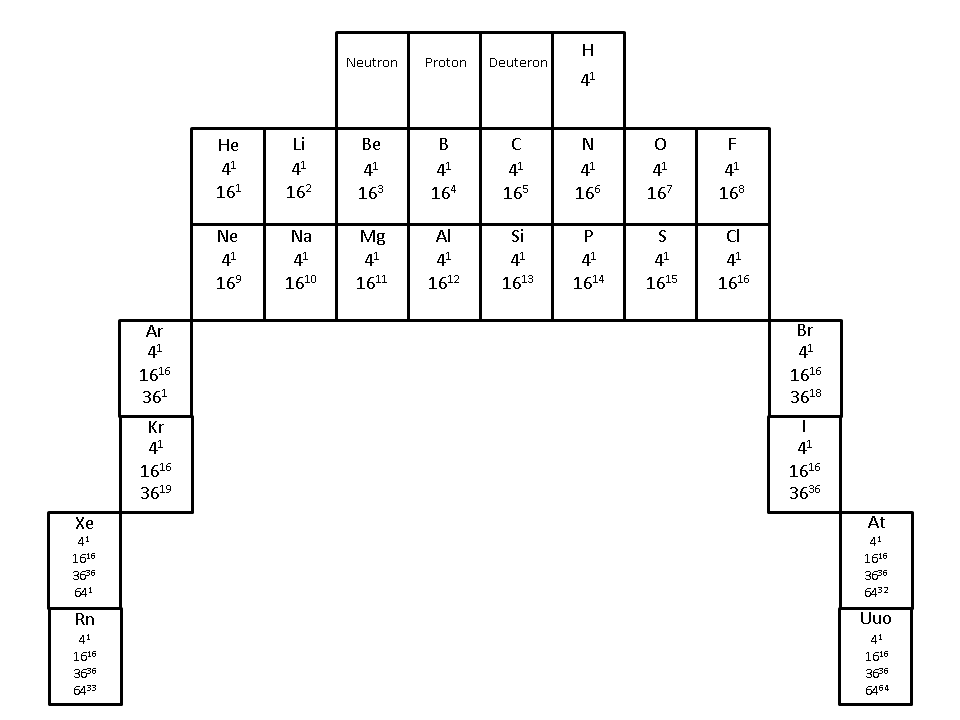
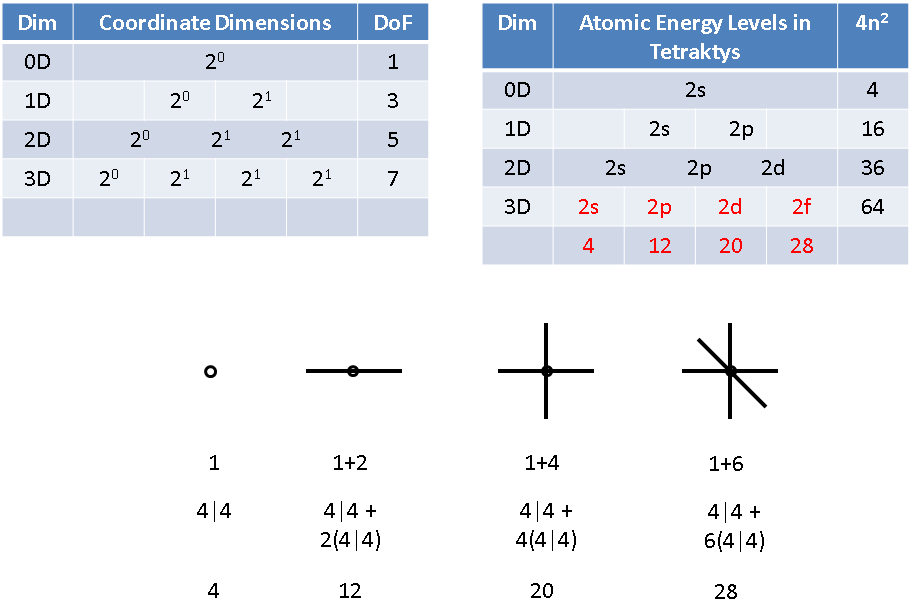
Here the table, like the wheel, is based on four, 4n² periods, where n = 1, 2, 3 and 4, respectively. Hence, the first row has four entities, the second and third have eight elements each, followed by two rows of 18 and two rows of 32 elements, although only the first and last element in the last four rows are shown, due to space limitations.

Of course, such a table is not of much use to chemists, since the groups of elements with similar chemical properties by column are not maintained. However, for understanding how our RSt generates the periodic elements, it serves better. Note how the number 4, designating the 4-entity row, has a superscript of 1, indicating the one electron of Deuterium. Each succeeding element also contains this electron, as its first electron, adding to it the electrons belonging to each of the next 16-elements of the double 8-row.

When these two rows are filled with 16 additional elements, the 18 elements in each of the next two rows that follow carry the full complement of electrons from the 4-row and the two 8-rows preceding them, designated as the 16, double row. The remaining elements follow suit.

Now, it's helpful to know how the LST treats the development of physical theory, from their perspective of vector motion, energy and momentum, but when it comes to the model of the atom, the scalar motion-based concept has to part ways with the LST concept dramatically, forcing us to think logically and philosophically, in a manner that is as consistent and powerful as Larson's was. It's a terrific challenge, but I'm forging ahead as best I can.

One of the grandest aspects of Larson's RSt, is how he treats the three dimensions of space and time. Electrical force is obviously 1D, magnetic force 2d and gravitational force 3d combinations of motion. I love the way he arrives at these conclusions mathematically, and I love the fact that Xavier Borg independently showed the validity of Larson's space/time dimensions from the formulas of the accepted SI dimensions, alone.

Consequently, the groundwork has been laid to help us discover how the combinations of motion that we have developed so far, which have been so successful in the 1D (electrical) realm, can be extended to the 2d (magnetic) and 3d (gravitational) realms. However, while the electrical aspects, like points on a line, are relatively easy to comprehend, in a reciprocal system, extending the reciprocal idea to 2d circles and 3d spheres is another thing altogether.

I imagine the center point of a space oscillation (unit circle, at -1 on the number line), combining with a time oscillation (unit circle, centered at +1 on the number line), according to our scalar motion equation, and wonder what that would entail. It must be that they have to be inverses of each other. Their product has to be equal to unit motion, and their sum has to be zero, the same as the analogous points, but how does that work?

We've been here before. In 2009, I showed how certain anomalies in the LST periodic table show up in the analysis of ionization potentials by Le Cornec. The late Albert Tarantola had "dismissed" Le Cornec's results, which he called a "second ordering of the elements" based on ionization potentials. He had long preferred a table introduced by Charles Janet, in 1929, which was based on the order of elements by atomic number, which Tarantola designated a "first ordering of the elements."

Both tables differ from the currently accepted periodic table, in the ordering of the elements, because the first ordering is based on atomic number (number of protons) and electron configuration, building up the atoms, proton-electron by proton-electron, and the second ordering is based on the ionization potentials, removing electrons, electron by electron.

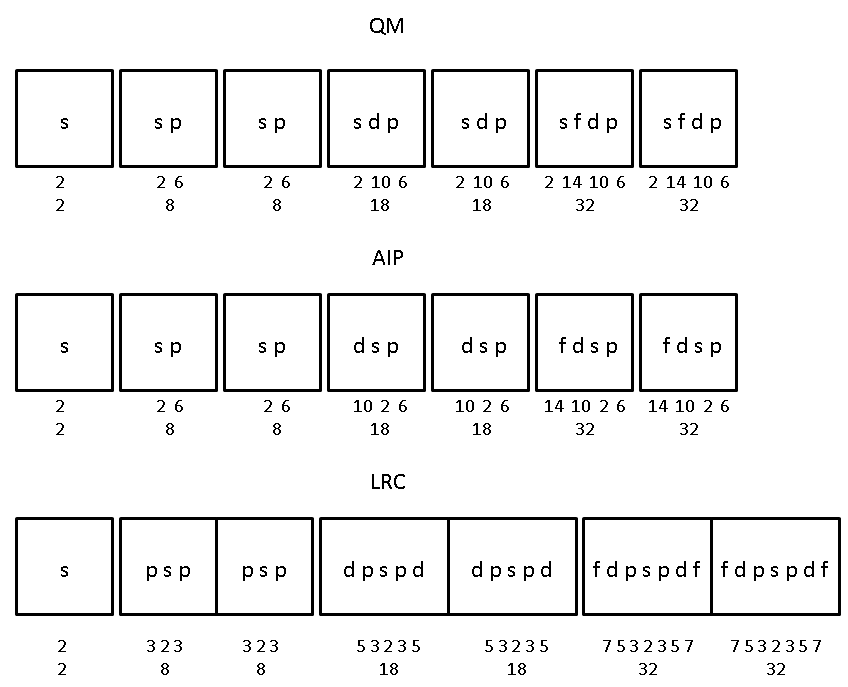
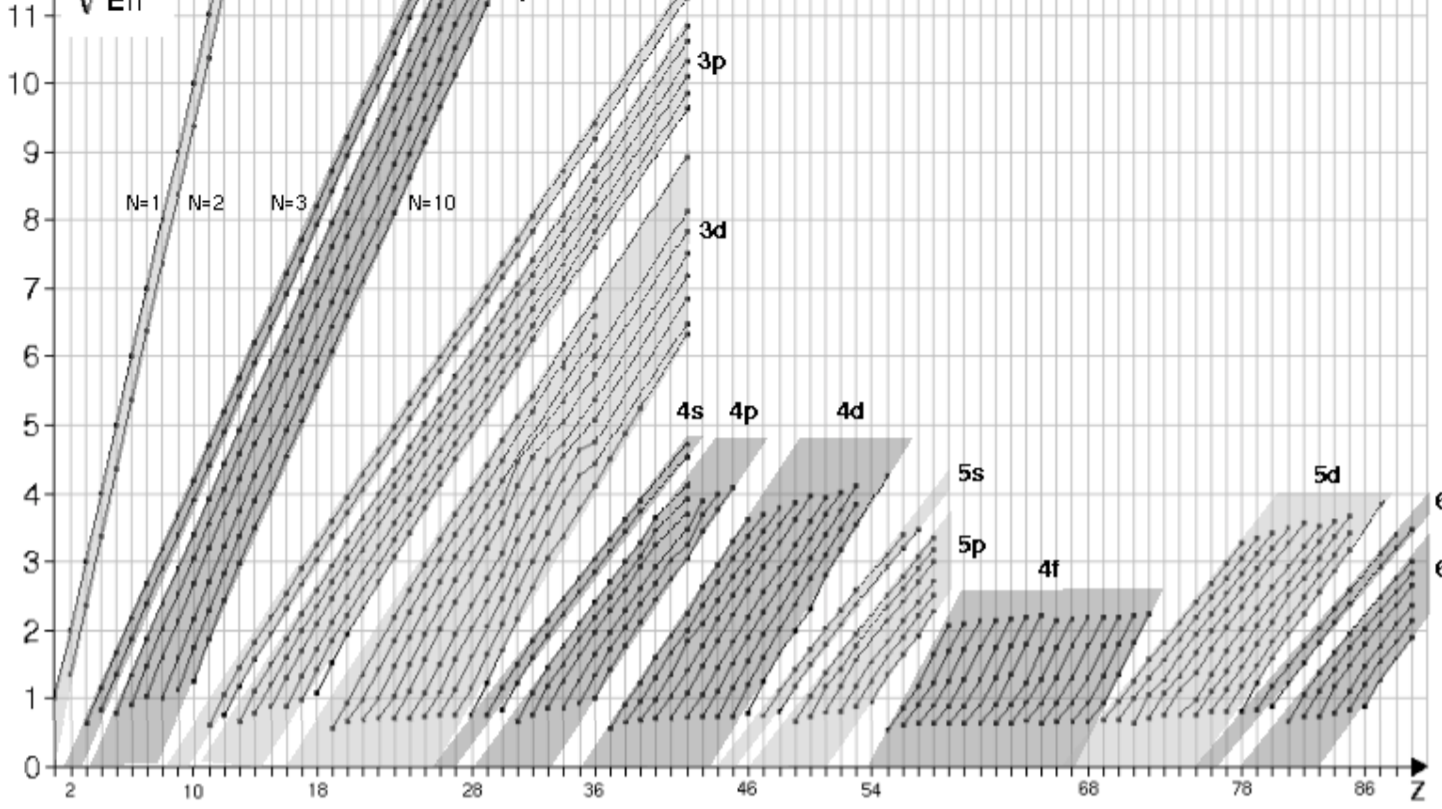
Tarantola explains the first ordering: "The order in which the energy levels of atoms is filled is well known: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p... Although not obvious, it is not hard to discover the regularity behind this list, and this regularity is expressed by the stair-like structure at the [foundation] of the Table, that has to be read in the normal reading sense (i.e., from top to bottom and from left to right). Placing in this ordered Table of Energy Levels the atoms that successively fill the energy levels (i.e., the consecutive atomic numbers) directly produces the 'Periodic' Table of the Elements."



This ordering is usually explained by chemists, as shown here by Paul Andersen, in this video. However, the underlying mathematics for this scheme is the Schrodinger wave equation, based on energy levels calculated from the total of potential and kinetic energy of electrons moving in certain "orbitals." It should agree with the reverse order of the energy required to remove these electrons from their atoms, but it does not. Here is the order of the elements found in the ionization data of Le Cornec:



As Le Cornec observed: "... the order of population of the different atomic layers in the standard model is 1s, 2s, 2p, 3s, 3 p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 5f, 5d, 6p, but the experimental evidence shows rather 1s, 2s, 2p, 3s, 3 p, 3d, 4s, 4p, 4d, 5s, 5p, 4f, 5d, 6s, 6p." Something is wrong!

Since the first ordering is theoretical, while the second ordering is empirical, we should see the LST community scrambling to revise the theory, but, of course, we don't. In a 2015 article, published in Science News, author Tom Siegfried explains how an "Old periodic table could resolve today’s element placement dispute," referring to Charles Janet's table. However, although Siegfried goes into quite a bit of detail on Janet's work, in the context of the energy levels of the table and their ordering, no mention is made of Le Cornec's iconoclastic results, which constitute much more worthy "scientific news" coverage than does the settling of disputes over the positions of certain elements in the order.

Needless to say, though, it should be highly regarded by us in our attempt to "remodel" the atom, in light of the RST.

More later.

[dbundy]

In considering the 2d and 3d forms of our 1d equation of motion. 1/2 + 1/1 + 2/1 = 4|4 num, we get into the subject of inversive geometry, where the inverse of the number line is generalized to what we might call a "number plane" and a "number ball," respectively. A better and more simple terminology, though, would simply be a 1d, 2d and 3d number line. The 1d number line is the set of rational numbers, where the unit value is the √1. The 2d number line is the same set, but with a unit value of √2, and the 3d number line is also, but with a unit value of √3, all three values stemming from the analysis of Larson's cube, already explained in previous posts. This, then, enables us to formulate the three forms of the equation of scalar motion, corresponding to each of the three dimensions:

1d --> √1/√4 + √1/√1 + √4/√1 =√16√16 num
2d --> √2/√8 + √2/√2 + √8/√2 =√32√32 num;
3d --> √3/√12 + √3/√3 + √12/√3 =√48√48 num

It's clear that the 1d form is straightforward: it's isomorphic to the group of rationals, where 1/1 is the identity element and the group is closed under all the usual operations, where each element of the group has an inverse element in the group. Geometrically speaking, this is just a reflection of a line. However, for the two higher dimensions, it's not so straightforward, unless one understands the basic principles of inversive geometry. Fortunately, there is a good video on this subject, and even though the A/V quality is poor, the content is excellent. See it here. It is a copy of a BBC and the UK Open University film.

Of course, we have to translate the geometric interpretation of lengths used in the film, with a datum of 1-1 = 0, like the R number set (the Reals), to the set of rational numbers, with the datum of 1/1 = 1. Also, the video only covers the 2d reflection of circles, and we need the 3d reflection of balls, or spheres, as well. Happily, there is not a lot of difference between the two.

Our objective is to deduce a new atomic structure, based on combinations of scalar motion that will accommodate the energy levels, which form the basis of the Periodic Table of Elements, as revealed, not by the electron configuration model of the Janet table, using the Schrodinger wave equation, but based on the Le Cornec table, using the NIST atomic ionization data (see previous post.)

Recall, how we have used the three scalar motion equations to formulate the respective quarks and fermions of each of the three families of our version of the standard model. Of course, only the first family, known in the LST community as the Electron family, is stable. We can call it the 1d family, while the other two, known as the Muon and Tau families in the LST world, would be our 2d and 3d families, respectively.

Given that our RSt posits these three families, based on the three scalar motion equations, for quarks and leptons, it follows that they also apply to the three bosons belonging to these families as well; That is to say, there are three dimensionally distinct W and Z bosons, as well as photons. We will call them 1d, 2d and 3d bosons and photons, and, as we have posited in the case of the constituent quarks of protons and neutrons, hypothesize that they play a role in the 1d family's combos, even though their own family is not stable.

If this is the case, then maybe we can find a dimensionally-based structure emerging from our atomic model, that follows the atomic ionization data presented by Le Cornec. Recall that the 1d equation for the proton,

S|T = 10/20 + 10/13 + 26/13 = 46|46 num,

combined with the 1d equation for the electron,

S|T = 6/12 + 6/3 + 6/3 = 18|18 num, equals

S|T = 16/32 + 16/16 + 32/16 = 64|64 num,

the 1d scalar motion equation for Hydrogen.

Taking the energy form of the equation of our 1d photon, where what Larson called the time-displaced oscillation is divided into what he called the space-displaced oscillation, we get the 1², 2², 3²...n², result, which is due to the balanced scalar motion equation, and which, as we have previously shown, follows the Rydberg equation for calculating the energy levels of the Hydrogen atom.

Notice that in that case we take the numbers in the equation to be isomorphic to the Reals; that is, Larson's time and space speed displacements are just the difference between the denominator and numerator. This means that the first one (1/2+1/1+2/1) is equivalent to 2/1 divided by 1/2, but, when we invert and multiply (2/1 * 2/1), we execute the operation using the displacement values, and so we get 1 * 1 = 1², instead of 2/1 * 2/1 = 2²/1. Then, the next increment is 4/2 * 4/2, where the two displacement values are 2, giving us 2², the next are both 3, giving us 3², and so on, up the n² energy sequence.

Unfortunately, while this works just as well as the stacked electron orbits of the Bohr model, it lacks the multi-dimensional features of the Schrodinger model that the Bohr model also lacks. The spherical harmonics of the Schrodinger wave equation managed to accommodate the s, p, d and f, magnitudes of spectral analysis, even though the Le Cornec results show something is not right with the model, because the positions are incorrect, as discussed in the previous post.

In short, Le Cornec has shown, in what C. K. Whitney calls “a stunning demonstration,” that the atomic ionization potentials exhibit a strikingly simple underlying pattern. The new pattern reveals that, while the elements are indeed grouped into the four 4n² periods (or eight 2n² sub-periods) exhibited by all these tables, the s, p, d, and f energy levels of spectroscopy repeat themselves in a different sequence than they do in the quantum mechanics theory. Le Cornec’s empirical pattern is:

s | s-p, s-p | d-s-p, d-s-p | f-d-s-p, (f-d-s-p),

while the theoretical pattern from QM, based on the four quantum numbers, n, l, m, s, and several rules of selection, is:

s | s-p, s-p | s-d-p, s-d-p | s-f-d-p, s-f-d-p.

Janet’s sequential pattern is the same as QM, but the energy levels are grouped differently, requiring the addition of two more elements at the end of the sequence in group s:

s, s | p-s, p-s | d-p-s, d-p-s | f-d-p-s, f-d-p-s.

Now, years ago, we noticed that these spectroscopy groups of energy levels map perfectly into the tetraktys:



This implies that the groups are somehow related to the three (four counting 0) dimensions of the tetraktys, with the 2s groups occupying the scalar slots along the left side, and the s, p, d and f groups occupying the pseudo-scalar slots along the right side. Tallying up the total numbers of electron slots of the groups from left to right, starting at the top, yields the 4n² numbers of the table periods. The numbers in the bottom row count the total numbers of each group in the 3rd dimension only. Note how they are evenly spaced by the number 8: 4-12, 12-20, 20-28. This will be significant as we go along.

More later.

[dbundy]

In the previous post we saw that the atomic spectra of the periodic table of elements has a three-dimensional (four counting zero) characteristic, as clearly shown by mapping the s, p, d and f energy groups to the tetraktys. Moreover, as the dimensions increase, from 0 to 3, the number of elements in the corresponding period increases as well, by 4n².

Now, this is another interesting instance of our favorite number 4 playing a central role in our theory. In fact, we can see that the value of the pseudoscalars, going down the right side of the spectral tetraktys, as we can call it, increases by 4n, where n = 1, 3, 5, 7: 0d = 1x4; 1d = 3x4; 2d = 5x4 and 3d = 7x4, or 4, 12, 20, 28, which is 4, modulo 8.

This is exceedingly curious, given John Baez's analysis of the Bott periodicity theorem, that "spooky fact of mathematics," as he calls it, which we have referred to many times over the years. His exposition of it is supposed to clarify why the periodicity of the tetraktys is modulo 8, proving there are no new phenomena beyond three, non-zero, physical dimensions. The numbers, 0, 1, 3, and 7 fall out of his analysis, and he excitedly emphasizes how curious that fact is, given that they are obviously one less than the dimensions of the Reals, Complexes, Quaternions and Octonions, or 1, 2, 4, 8, which we now know pertain to the "directions" of the three (four) dimensions of the tetraktys, not its dimensions.

However, we also see that the n series of numbers, 1, 3, 5 and 7, the factors of 4 in the spectral tetraktys, are one less than the square root of the four periods of the periodic table, relating them to the modulo 8 of Bott periodicity, as well; that is to say, modulo 8 not only holds for the dimensional "directions" of the tetraktys, as Baez correctly notes, but it also holds for the dimensional structure of the atom, as seen through its spectra. In the words of Baez, "Bott periodicity strikes again!"

Since four natural units of motion (num) is the minimum value of our first combo (1/2 + 1/1 + 2/1 = 4|4), we conclude that there might be a connection with the tetraktys and our scalar motion combos that will lead us to the dimensional structure we are looking for in the atom. Indeed, it appears that, just as the concentric circles of the wheel of motion provide an increased degree of freedom as the radius of each circle increases, the degrees of freedom of the scalar motion equation may also increase with increasing num.

For example, if we consider s/t (t/s) = 1/1, the unit progression, we see that it has only one degree of freedom, 1/1 = 1. However, if we consider the same thing as 2/2, we see that it has three degrees of freedom: 1/2, 2/2, 2/1, while 3/3 has five degrees of freedom: 1/3, 2/3, 3/3, 3/2, 3/1. Finally, 4/4 has seven degrees of freedom: 1/4, 2/4, 3/4, 4/4, 4/3, 4/2, 4/1.

These are the same degrees of freedom used in the Schrodinger wave equation, which come from the mathematics of spherical harmonics, used to define the s, p, d and f orbitals of the LST's atomic model. In effect, they are the four dimensions of the tetraktys manifesting themselves in the form of energy. We can use the LST model as a guide to illustrate the concept, but adopt our new model to the Le Cornec results, hopefully.

First, let's map the groups to the tetraktys in more detail:



Figure 1. Top graphic: Spectral Tetraktys -- Lower graphic: Electron Configuration for Hydrogen

In figure 1, we again see how the spectra groups map to the dimensions of the tetraktys and the periods of the periodic table. Below that, the electrons of each group are laid out: the s groups are black, the p groups are green, the d groups are blue and the f groups are red.

The degrees of freedom are indicated in the left-most column, while the number of electron slots in each degree is indicated in the right-most column, with the atomic number Z shown in the bottom row.

The red fill color indicates an electron populating a given dimension. In this case, the one electron of Hydrogen is shown in the 0 dimension with 1 degree of freedom. The configurations for Helium through Fluorine follow: (Errata Note: the two red f groups consist of 14 electron slots each, not 10, as shown in these graphics.)






The graphics don't show it clearly enough, but it should be understood that each group is a double set: 2s (2&2), 2p (3&3), 2d (5&5) and 2f (7&7), although if we treat the 2s group as a single group, instead of a double group, then the correct number of degrees of freedom in each dimension is quite evident, and this makes a lot of sense in our RSt, because 4 is the minimum number of num that can form a combo.

In fact, on that basis, we can rearrange the groups to clearly show that the dimensional increase follows the s/t (t/s) pattern, as given in the example previously:



This is a stunning illustration of how the atomic spectra is indeed a dimensional structure that conforms to the mathematics of the tetraktys and Bott periodicity. As the degrees of freedom increase with each dimension, the number of electron slots (atomic elements) increases, accordingly. We begin with four slots at the top, or 0 dimensional level, with only one combo accommodating an electron, the combo Deuterium. At the 1 dimensional level, the number of electron slots (elements) increases by 12, from 4 to 16. Dimension 2 increases the freedom by 20 more, giving us a total of 36 in that dimension, while dimension 3 increases the freedom by 28 more, giving us 64 in the last dimension.

I think we are now one step closer to understanding the new scalar motion atomic model.

[dbundy]

As far as I know, yesterday was the first time ever, an alternate to the LST's atomic model, based on the Schrodinger wave equation, has ever been published. Of course, it's not going to be acknowledged as such until the day comes when the LST admits that scalar motion is real. Nevertheless, we've clearly reached a milestone in our RST community.

In the new, scalar motion based, model, we have the same rules of selection that the LST model has, namely the four so-called quantum numbers, n, l, m_l and s. The first one is n, the principal quantum number or energy level. The next is lowercase L, which is the value of the electron's angular momentum. The third is m sub L, which is the number assigned to the spectra groups, s, p, d and f, and the last one is s, the quantum spin. A good video explaining how these numbers are used in the LST model is here.

All of these numbers are also found in our new scalar motion quantum model, as shown below:



In the next post, I'll will attempt to show how we can follow the Le Cornec data to populate the model with electrons.

[dbundy]

The next step in our development of a scalar motion atomic model that can accommodate the energy levels of the atomic spectra, which we have shown to be related to the dimensions, "directions" and format of the tetraktys, is what the LST calls "electron configuration;" that is, we need to show how the electrons are configured within the atom, in such a way as to account for the observed line spectra for each element.

As already mentioned, this challenge is complicated by the published Atomic Ionization Potentials (AIP), which Le Cornec shows can be tabulated to show a different configuration than the LST's configuration, when the square root of the ratio of the element's Z number, with that of Hydrogen, is calculated.

Le Cornec asserts that the AIP data shows that "the complex mathematical shape of quantum mechanics is in real contrast with the simplicity of the AIP distribution. Obviously," he writes, "'God does not play dice' with the ionization potentials, at least, and we may wonder if quantum mechanics will be able to explain the AIP measures without some simplifications."

Well, actually that is a tall order, but the whole purpose of Larson's reciprocal system of scalar motion is to do just that: It purports to simplify the physical picture. Hence, if we can extend what we have accomplished at the LRC, using Larson's system, to simplify our understanding of the atomic spectra, it will be a wonderful day for our community. Unfortunately, we are not there yet, but we are making significant progress.

First, let's compare the LST electron configuration with the AIP configuration and then the LRC configuration:



In the graphic above, we can see that the difference between what the empirical data shows in the order and what the wave equation, based on the LST's four quantum numbers, shows, is a difference in the sequence of the spectra groups, s, p, d and f. What both orders have in common, however, is the duality of the groups. The LST breaks these down into the familiar list of orbitals and energy levels, and using the so-called "diagonal rule", the order is determined, as shown in our graphic.

However, this order does not conform to the AIP empirical data shown below it. If we were to take the same approach with this data, as the LST does with the wave equation calculations, we would have to use a "horizontal rule," which would work part way, but then it breaks down.

As shown in the two previous posts, the LRC approach is to recognize the spectral tetraktys, wherein we map the spectra groups to the dimensions and format of the tetraktys. On this basis, three out of the six energy slots in the p group are placed on either side of an s group. Then five out of the ten slots in the d group are placed on either side of these. Finally, seven out of the fourteen slots in the f group are added to both sides of these. When we do this, not only is the total number of energy slots fixed by the dimensions of the tetraktys (see the ? marks in the graphic linked to above,) but the order is also fixed. At least I thought so, until I tried to fill in the slots, according to the AIP data!

According to these values, starting at the highest value for a given element, the first slot in a p group is filled by the fifth electron in Boron, the last one with the least energy:



The first thing to notice, of course, is the first s group at the top, where n = 1. The two vacant slots are vacant because they are not slots for electrons, but the last two are. The bottom left of the four is the slot on the first line of the AIP plot (Hydrogen), while the bottom right slot is the second line of the plot. Both slots are populated for Helium, with the value of the left one showing 2. The boxes are too small to place the numbers in, so the number appears in a separate, larger, box with an arrow pointing to the first slot.

The selection rule, for now, is, populate the left slot first, then the right slot, in each row, starting with the s slots, until that row is full. Each slot will have its own number, indicating the energy value of that slot for that element (only the first slot value appears in these graphics.) Therefore, in the graphic above for Beryllium (Z = 4) (misspelled on the graphic) and Boron (Z = 5), there are four and five slots filled, respectively. The energy value for the first s slot at the top actually comes from the AIP data plot. It just happens to match the Z number, due to the square root of the Z ratio, used by Le Cornec.

As it turns out, there is no way to get the lowest energy electron of Boron to populate the first p slot, as the data shows it does, without populating the last two slots of the first s group at the top, with H and He. This means He is the last element of the 4n² period, when n = 1 and Li is the first element of the period when n = 2. So, Ne and the other noble elements are at the end of their respective 2n² half-periods.

Continuing to populate the energy slots, first left, then right, along the s and p half-groups, the first row of s and p is filled at Z = 10, Ne, with a first electron energy value of 10, and the next row begins to be populated with Na, at Z = 11 and energy at 11:



The first slot to be populated in the Na row is the left one in the next s group, as indicated by the AIP plot for Sodium. The s & p rows continue to be populated following the left | right rule, until we reach Ar, Z=36. It is at this point that trouble begins, because the first element of the next period to be populated, where n=3, is K, Potassium, and the plot shows that its electron populates the first slot of the d group, not the s group, as in the rows above it! I don't know how to explain this. It's as if there is some kind of rule that s & p always have to go together and s has to be filled first!

Not only that, but after the two d half-groups are filled, from the outside in (an arbitrary choice for now) the electron of the next element to be populated (Cu, Z=29) is placed in the first slot of the s group, not the p group, as would be expected!



This pattern completes with Krypton, and the next element, starting the second half of the 36 element period, Rubidium (Rb, Z=37), repeats the same strange way. This s & p behavior also holds true for the two half-periods of the next full period, beginning with Caessium (Z=55):



As yet, I have no explanation for this "swapping order" of the s & p groups, as I'll call it for now, but I'm happy with what has been achieved to this point anyway. Here's a legible copy of Le Cornec's data plot:



AIP Data

[dbundy]

One of the most important discoveries in our theoretical development has been the connection between the dimensions of the tetraktys and the geometry of the 2x2x2 stack of unit cubes we call Larson's cube (LC), and now that we see the connection of the atomic spectra and periodic table to the dimensions of the tetraktys and its associated degrees of freedom, we are naturally curious to know if we can extend it to the LC, as well.

Of course, the LC is the geometric basis of our scalar motion combos, the most fundamental of which we write mathematically as four units of motion: 1/2 + 1/1 + 2/1 = 4|4 num. Now it may be just another in a very impressive series of coincidences, but, in terms of the degrees of freedom, 1, 3, 5 and 7, which result from the four dimensions of the tetraktys, wherein we've seen the modulo 8 phenomenon of Bott Periodicity emerging, the equation is a perfect fit:

4|4 = (1 x 4|4) = 4|4;
4|4 + (2 x 4|4) = 12|12;
4|4 + (4 x 4|4) = 20|20;
4|4 + (6 x 4|4) = 28|28;

Again, the factors 1, 3, 5 and 7 show up in those terms of the scalar motion equation, answering to the s, p, d and f groups of the atomic spectra, as shown in the previous post. However, the 1, 2, 4 and 6 factors, which it takes to get us there, differ from the 1, 2, 4, 8 numbers of the binomial expansion of the tetraktys that we are so accustomed to using, the powers of 2.

Now, this was a little disconcerting at first, until it dawned on me that it does follow the dimensions of the LC, when we consider its coordinate dimensions, as opposed to its binomial dimensions. Its binomial dimensions are multiplicative. as powers of 2: 2⁰, 2¹, 2², 2³, or 1, 2, 4, 8, but its coordinate dimensions are additive: 2⁰, 2¹, 2¹+2¹, 2¹+2¹+2¹, or 1 unit (a 2⁰ point), 2 units (along 1 axis, in opposite "directions"), 2 units (along 2, perpendicular, axes, in opposite "directions") and 2 units (along 3, perpendicular, axes, in opposite "directions").

When we plug these coordinate units into the tetraktys, we get the same dimensional structure in it, as we do with the usual binomial, multiplicative, units, but it also reflects the same coordinate axis structure of the LC, implying that we can easily map the s, p, d and f groups into the LC:



Some people say that they don't believe in coincidences, yet I have seen uncanny ones many times. However, I have never seen a long series of them, consistent with a rigidly structured set of mathematical, geometric and logical principles, such as those we are dealing with in the development of our RSt.

It's very, very impressive to my mind.

[dbundy]

John Baez is a smart guy, and I've quoted him many times on Bott Periodicity. Bottom line, he says he's "shocked" that "something so basic-sounding as 'dimension' should be related to something so erudite-sounding as the 'octonions'!

However, what he and his fellow mathematicians have failed to recognize is that what they call "dimensions" are actually the "directions" of dimensions, and what Bott periodicity is about is the fact that, physically, there are no more than three non-zero dimensions. What the number 8 of Bott periodicity (and the namesake of the Octonions) has to do with dimension is that it represents the limit on the number of "directions" and thus the number of the dimensions of nature.

Baez's discussion of the subject is clothed in the usual obscurity of formal mathematics, but the simple truth of it can be clearly understood by the connection between the tetraktys and the LC. The graphic below depicts it:



The number of non-zero dimensions is limited to 3, and thus the number of dimensional "directions" is limited to 2³ = 8. What is not limited is the magnitude that can be expressed in the three dimensions and their eight associated "directions."

At unity, the magnitude is equal to the number of "directions," but beyond unity, the duality of the "directions" of each dimension becomes a factor of n: 2x1=2, 2x2=4, 2x3=6, ...2xn=2n. Hence, when we repeat the calculation of the tetraktys for each n => 1, the result follows the progression of the LC, as can be seen in the graphic.

What's interesting to us now that we have found the Bott periodicity in the groups of the atomic spectra, which enables us to graph them in the spectral tetraktys (see previous posts), is the fact that each time we advance the Bott period, we increase n by the power of three, as shown by the numbers under the successive tetrakti, indicated in the graphic above.

Consequently, we conclude that the dimensions, "directions" and magnitudes of the LC and the tetraktys progressions unify algebra, as the science of numbers, with geometry, as the science of right lines and circles, in a way that would have presumably excited Hamilton.

Yet Baez et al, having confused "directions" with dimensions and taken the route of imaginary numbers to construct number systems of higher dimensions, don't view the dimensional periodicity this way. Instead, they see the periodicity in terms of increasing dimensions (actually "directions"), instead of increasing magnitudes, as depicted in the graphic. The illustration he uses in his article is in the form of an eight hour clock:



Here we see that at hour 4, the dimensions ("directions") have increased from 2³ to 2⁴, where they place H, the symbol for quaternions (the symmetry he mentions in the text evidently goes along the 2 0'clock - 7 0'clock axis.) Thankfully, he distinguishes in the text between the dimensions of space (0, 1, 2 and 3) and the dimensions of Clifford algebras (1, 2, 4 and 8), which we call "directions."

Since Clifford algebra dimensions double with each higher dimension, at 2⁴, what we call "directions" would have increased to 16, which is a violation of the Bott periodicity theorem, limiting the dimensions of space to 3 in number and therefore the "directions" to 8 in number, but they get around this problem by reverting to matrices. If we are correct, the 8 hour clock should be modified to look like this:



Now, the reflection symmetry is perfect, all around the clock. Not only this, but we don't have to employ Clifford algebras in matrices to get around the problem of non-associative octonions, although I've kept the same designations used for the normed division algebras. The caveat is that they should be understood as 0d, 1d, 2d and 3d scalar algebras not imaginary number- based normed division algebras.

I don't know how useful this clarification will be in attacking our current challenge, but I thought it was worth pointing out.

[dbundy]

After thinking about it further, I realized that the new modulo 8 clock posted above could be enhanced to match the tetraktys - LRC graphic even more, by adding the notion of the progression of the radii of the LRC's inner ball to it, the magnitude of which is the √1. Since the progression is based on the two "directions" of each dimension, n (or in this case r) is doubled at each step, and the magnitude for each dimension ends up being equal to the diameter of the ball (2r):



On this basis, r is the dimension of time and increases as n = 1, 2, 3, ...∞, in the progression. This is a much easier, efficient and compact way to depict the progression of the Tetraktys - LRC. No more drawing stacks of cubes! My gratitude goes out to John Baez!

And there is no reason to stop there either, as we could add the 2d radius (√2) and the 3d radius (√3) to the clock, if we wanted to show the complete picture, or maybe just note the three values of r to be used, depending upon the particular dimension of the round being considered.

Of course, this is not the whole story. More to come later.

[dbundy]

With the new diagram posted above, combining the dimensions, "directions" and magnitudes of the tetraktys and the geometry of the LC with the Bott periodicity theorem adapted from John Baez's online article on the octonions, we have, in one image, a composite picture of the mathematics, geometry and logic of the LRC's RSt.

It's also very instructive to use it to compare and contrast the vector motion of the LST and the scalar motion of the RST, and how the two different concepts fundamentally affect the mathematics and science of the two systems of theory. Due to the fact that motion in the LST is conceived as a change of position in physical space, the mathematics of the LST follows suit, by conceiving algebra in terms of change of position in abstract space.

In contrast, motion in the RST is defined without regard to the changing position of objects; It is simply the relation between expanding/contracting space and expanding/contracting time. This is a radical difference, which we usually characterize by stating that, unlike the vector motion of the LST, which has both magnitude and direction, the motion of the RST is motion of magnitude only. It expands/contracts in all "directions" of a given dimension.

In algebra, the direction property of numbers is manifest in its operations. These operations are polarized, so that 2-3 is not the same as 3-2; that is, the result of the two operations places us in two different positions along the number line: -1 and +1. However, this is fairly easy to comprehend in one dimension, because it's much like our physical motion, where one direction of travel is the opposite of another, and we have to reverse direction to return to the origin. When we consider two dimensions, though, the reasoning becomes a bit more sophisticated and requires a rotation operation to "travel" between these two positions on the number line. In three dimensions, it is much more difficult to understand and even controversial.

The bottom line is that algebraic operations on numbers are complicated by the LST's connection of motion to change of position in two "directions" of each dimension. The complication becomes exacerbated as the dimension of the numbers increases, from 0 (points on a line) to 1 (distance between points on a line), to 2 (area between lines), to 3 (volume between areas).

Ingenious mathematicians have found ways to cope with these complications over the centuries, by devising rules of logical operations, but in the process have discovered that there are truths of nature that numbers and operations upon them reveal to be hidden deep within the ordinary experience of man.

Reciprocity is one of those hidden truths, and, as it turns out, the new diagram incorporates it nicely. In other words, in the one Bott cycle of 8, it encompasses two copies of the tetraktys - LC, and one of these is the reciprocal of the other:



Notice that this diagram is a revised version of the previous one posted above, where the notation now indicates the geometry of a respective dimension rather than the applicable normed division algebra. In essence, two copies of the tetraktys - LC, one the reciprocal of the other, are included in one Bott cycle, which answers to our new scalar equation, where two, reciprocal LCs are joined together.

Of course, the comparison with a clock in the original form is somewhat misleading in the revised form, where the radius, r, remains constant for a given interval, affecting all magnitudes simultaneously. When r changes, all values are thus affected together, according to the value of r.

[dbundy]

If the reader wants to review page 3 of the posts above, where I explored the progression of the tetraktys - LC in terms of poles, it will perhaps be helpful in the present context. There, we were discussing the connection of the tetraktys to Pascal's triangle and the LC progression, thinking that the progression of the three families of our version of the standard model, the electron, muon and tau families, could be explained in terms of multiples of the number of poles in the tetraktys.

However, that tentative conclusion was based on a misunderstanding of Bott periodicity, which at the time I thought meant a repeat of the tetraktys, given that the 8 dimensions involved were actually the 8 "directions" of the fourth normed division algebra, the octonions, which the mathematicians consistently confuse with physical "dimensions."

However, now I realize that's not the case. When they talk about Clifford algebras, which they do when explaining Bott periodicity, the word dimension does not refer to the "direction" of the normed division algebras, 1, 2, 4 and 8, but the dimensions of geometry, 0, 1, 2 and 3! Thus, the dimensional 8-unit "clock," which I have borrowed, goes from 2⁰ to 2⁷, before it repeats, not 2⁰ to 2³, as I had thought, due to the careless way they employ the word "dimension."

Baez doesn't bother to explain this explicitly, as far as I know. Usually, especially when addressing mathematicians, as in a series of comments he made in response to a post reviewing his article in Scientific American on octonions and string theory, posted at the Not Even Wrong website of Peter Woit's, he uses the word "dimension" in the mathematical sense. For example, he refers to a "magical identity that holds only in spacetimes of dimensions 3, 4, 6 and 10," which is explained, he says, in a highly authoritative string theory textbook. It turns out that a loop of string moving in time introduces two extra dimensions (think of the 2d wall of a tube), which are added to the dimensions of "spacetimes," which. of course, must then be 1, 2, 4 and 8, matching the "dimensions" of the normed division algebras, his favorite subject.

However, in explaining Bott periodicity, in terms of Clifford algebras (see his article linked to above), the dimensions of the algebras are only referred to as a number, n, not dimensions:

C0 = R

C1 = C

C2 = H

C3 = H + H

C4 = H(2)

C5 = C(4)

C6 = R(8)

C7 = R(8) + R(8)

C8 = R(16)

Hence, the "8 hour clock" is introduced as a way to remember the dimensions of the above list of Clifford algebras, in terms of combinations of normed division algebras. This is maddening, because I don't know if they don't recognize that every dimension has two "directions" or not. They never talk about it that I know of. Consequently, according to Bott periodicity, we have two copies of the tetraktys occurring every 8 increments of Clifford algebra dimensions, but these are a repeat of the four (counting 0) geometric dimensions of the tetraktys, not the confusing mathematical dimensions of the mathematicians.

Consequently, I have to now revise the work found in the entries on page 3 of this topic, but the good news is this equivocation has given us a clearer insight into Bott periodicity, and, hopefully, it connects with the spectral tetraktys and the dimensions and numbers of the spectroscopy groups and the periodic table we are now investigating.