Since comparing the properties of entire ratios (units of motion) is the only operation that makes sense in the scalar realm, then comparing their aspects individually does not make sense there. Because over the span of one ratio, the speed is always the same, the only property that can vary between ratios are their delta signs. Thus the only difference that two units of motion can have, are their signs and their order in the progression. Two consecutive identical signs tell us that the ratio is the same as the previous ratio in the progression order.
These observations allow for certain homotopic transformations to be performed on the graphs, namely they allow us to flip BOTH signs in any row of the PA graph and do not change anything from the scalar standpoint, because the resulting sign of the entire ratio does not change under such transformation. Flipping the sign of just one aspect, does change the sign of the ratio though, so it is disallowed, ...unless you are considering only one ratio in complete isolation, where the sign of this ratio is not related to the sign of another ratio so nobody cares about it and it just doesn't matter. The only use of the latter case, that I can see, is in teaching activities or in formulation of the Fundamental Postulate.
Flipping both the numerator and denominator sings in a ratio, changes nothing in the scalar realm, but it does affect the integration of multiple units. The latter is where the most of the variability is.
The animation below shows the result of such homotopic transformation at row 4.
Note that the ratio of the last row is 6/8 before the transformation and 4/9 after the transformation. That last row represents the result of an integration over 9 stages of progression.
I could make these transformations on any rows of the PA graph and did not change anything from the scalar standpoint, but it would change the result of the integration.
Below is a different motion (series of ratios) that is being gradually normalized to uniform unit time, from top to bottom, using the same signs-flipping transformations. Q:Who does such normalization in nature ?
A: The observer does (that's why c-Krypton is our material Muon)
Relativity of "Direction"
Moderator: dbundy
Re: Relativity of Direction
(Note this was written in connection with my previous comment. I had not seen your post above at that point. I will respond to that one, after I have had a chance to study it.)
I would like to point out, however, Horace, that I have maintained for a long time, it's important to remember that for each dimension there is a factor of two "directions," (21 = 2, 22 = 4 and 23 = 8), as shown both in the tetraktys and in Larson's cube.
That these are "directions" and not directions (in space or time), means that they are background independent. Thus, a scalar expansion/contraction, in a given set of dimensions, expands/contracts in all the "directions" of those dimensions, simultaneously, by definition:
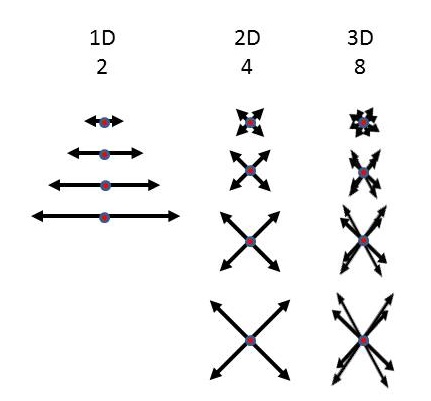
Again, no background is necessary to give meaning to these "directions." They are the inherent properties of the dimensions of a given magnitude.
I would like to point out, however, Horace, that I have maintained for a long time, it's important to remember that for each dimension there is a factor of two "directions," (21 = 2, 22 = 4 and 23 = 8), as shown both in the tetraktys and in Larson's cube.
That these are "directions" and not directions (in space or time), means that they are background independent. Thus, a scalar expansion/contraction, in a given set of dimensions, expands/contracts in all the "directions" of those dimensions, simultaneously, by definition:

Again, no background is necessary to give meaning to these "directions." They are the inherent properties of the dimensions of a given magnitude.
Re: Relativity of Direction
I have no problem with that, but note that this refers to the direction of a change.dbundy wrote: I would like to point out, however, Horace, that I have maintained for a long time, it's important to remember that for each dimension there is a factor of two "directions,
Change requires history. History requires time. Altering the direction of time also alters the direction of history ...and the direction of the change with it.
So although one dimension of change indeed has two directions, these directions are more ambiguous than one might expect when the customary restriction of unidirectional time is assumed.
That would be properly named "pseudoscalar" in Geometric Algebra's jargon, when the number of dimension is "given" and all used up.dbundy wrote: Thus, a scalar expansion/contraction, in a given set of dimensions, expands/contracts in all the "directions" of those dimensions, simultaneously, by definition
Yes, no background is necessary but a "past" reference is needed to define any change. If you alter that reference then the "direction" of the change will not stay the same.dbundy wrote: That these are "directions" and not directions (in space or time), means that they are background independent.
Again, no background is necessary to give meaning to these "directions." They are the inherent properties of the dimensions of a given magnitude.
Re: Relativity of Direction
Horace, this is a radical departure from my way of thinking about the consequences of the postulates. I'm open to learning more about it, but at this point I am skeptical.
I understand how a homotopic transformation maps a change in form, but we are not talking about changes in forms (geometry) here, I am not convinced of your conclusion that "comparing the properties of entire ratios (units of motion) is the only operation that makes sense in the scalar realm."
The properties of the two aspects of a vector motion, let's say the motion of a pendulum, are clearly comparable, or related in a definite way that constitutes a law of physics, which can be analyzed in terms of geometry and dynamics.
Now, when it comes to the scalar motion of objects, the same situation applies. We can analyze a change of scale in terms of geometry and dynamics. Hydraulics might be an example, where scalar values of volume and pressure enter into the calculations, in a way that has little to do with change in position.
So, when we enter the realm of the RST, where there is no object, but only an abstract concept of an initial state of expanding space and time, we are more dependent upon logic and numbers than ever. I think we have to proceed step-by-step, ensuring that our deductions are sound, as much as we possibly can.
One of the most important principles to keep in mind, I think, is known as the "Trichotomy Law." It's just a modern word for what I have already pointed out: A number, a magnitude, a value can be one of three things. It can be equal to another number, magnitude or value, or it can be more than it, or less than it. The only whole number less than 2/1 (1) is 0 (1/1), if we can call it a number, but this is true only if we don't change "directions" on the number line. Changing to the opposite "direction," on the other side of 0 (1/1), the only inverted whole number less than 1/2 (-1) is again 0 (1/1).
The only other way to change signs is to reverse the "direction" of a change toward 0 to a "direction" away from 0. This, of course does not require crossing 0, but it should be understood in the sense of the reference to 0. Otherwise, I can't see how we can progress (no pun intended).
Changing signs requires changing "directions" and that requires crossing over unity (0), or using it as a reference. It seems to me you have thrown that law out of the picture. Which, BTW, is exactly what the LST community did in their application of complex numbers to quantum mechanics.
I understand how a homotopic transformation maps a change in form, but we are not talking about changes in forms (geometry) here, I am not convinced of your conclusion that "comparing the properties of entire ratios (units of motion) is the only operation that makes sense in the scalar realm."
The properties of the two aspects of a vector motion, let's say the motion of a pendulum, are clearly comparable, or related in a definite way that constitutes a law of physics, which can be analyzed in terms of geometry and dynamics.
Now, when it comes to the scalar motion of objects, the same situation applies. We can analyze a change of scale in terms of geometry and dynamics. Hydraulics might be an example, where scalar values of volume and pressure enter into the calculations, in a way that has little to do with change in position.
So, when we enter the realm of the RST, where there is no object, but only an abstract concept of an initial state of expanding space and time, we are more dependent upon logic and numbers than ever. I think we have to proceed step-by-step, ensuring that our deductions are sound, as much as we possibly can.
One of the most important principles to keep in mind, I think, is known as the "Trichotomy Law." It's just a modern word for what I have already pointed out: A number, a magnitude, a value can be one of three things. It can be equal to another number, magnitude or value, or it can be more than it, or less than it. The only whole number less than 2/1 (1) is 0 (1/1), if we can call it a number, but this is true only if we don't change "directions" on the number line. Changing to the opposite "direction," on the other side of 0 (1/1), the only inverted whole number less than 1/2 (-1) is again 0 (1/1).
The only other way to change signs is to reverse the "direction" of a change toward 0 to a "direction" away from 0. This, of course does not require crossing 0, but it should be understood in the sense of the reference to 0. Otherwise, I can't see how we can progress (no pun intended).
Changing signs requires changing "directions" and that requires crossing over unity (0), or using it as a reference. It seems to me you have thrown that law out of the picture. Which, BTW, is exactly what the LST community did in their application of complex numbers to quantum mechanics.
Re: Relativity of Direction
In my opinion, that's what is required to progress. As the old airmen used to say "If you're not getting any flack, you're not over the target".dbundy wrote: Horace, this is a radical departure from my way of thinking
I'm not changing the postulates.dbundy wrote: about the consequences of the postulates.
That all right but you cannot refute my logic.dbundy wrote: I'm open to learning more about it, but at this point I am skeptical.
Yes and no. "Yes" because the PAs are geometric constructs. "No" because there are no geometric constructs in RST scalar realm.dbundy wrote: I understand how a homotopic transformation maps a change in form, but we are not talking about changes in forms (geometry) here,
Then state unambiguously, what else can be compared, so I can have something concrete to argue against.dbundy wrote: I am not convinced of your conclusion that "comparing the properties of entire ratios (units of motion) is the only operation that makes sense in the scalar realm."
Yes, but I was not writing about vectorial motion lately.dbundy wrote: The properties of the two aspects of a vector motion, let's say the motion of a pendulum, are clearly comparable, or related in a definite way that constitutes a law of physics, which can be analyzed in terms of geometry and dynamics.
No, because we do not have a unidirectional uniform growth of time in the scalar situation, like with the vectorial motion you just mentioned above.dbundy wrote: Now, when it comes to the scalar motion of objects, the same situation applies.
Objects? What "objects" ? At this stage of development there are not objects yet and if there are they are scalar motions, too.
No, there is no geometry in the scalar realm, because there is no preferred direction - there is only growth or shrinkage.dbundy wrote: We can analyze a change of scale in terms of geometry and dynamics.
I was not writing about a change of position lately - only about the relativity of growing and shrinking.dbundy wrote: Hydraulics might be an example, where scalar values of volume and pressure enter into the calculations, in a way that has little to do with change in position.
Also, I challenge you to illustrate the immutability of scalar direction using the ratio of "scalar values of volume and pressure" without involving time.
That's exactly what I was doing. I hope you did not construe my attempts to graph scalar motion as an attempt to impose geometry on scalar motion.dbundy wrote: So, when we enter the realm of the RST, where there is no object, but only an abstract concept of an initial state of expanding space and time, we are more dependent upon logic and numbers than ever. I think we have to proceed step-by-step, ensuring that our deductions are sound, as much as we possibly can.
I agree with the Trichotomy but I don't understand why you consider it to be so important. I think that it is more important that this Trichotomy requires at least TWO numbers to compare. Change is born from comparison.dbundy wrote: One of the most important principles to keep in mind, I think, is known as the "Trichotomy Law." It's just a modern word for what I have already pointed out: A number, a magnitude, a value can be one of three things. It can be equal to another number, magnitude or value, or it can be more than it, or less than it.
Yes, but why is it a prerequisite for 2/1 > 1/1 and how does that invalidate that 1/2 < 1/1 ? Also, on 1 unit level you don't even have speeds other than +(1Δ/1Δ) or -(1Δ/1Δ) so considering numbers other than ±1 is a misunderstanding with individual units of motion.dbundy wrote: The only whole number less than 2/1 (1) is 0 (1/1), if we can call it a number, but this is true only if we don't change "directions" on the number line.
Please be precise. The direction of what? Direction of the ratio or of the aspect/aspects ?dbundy wrote: The only other way to change signs is to reverse the "direction" of a change toward 0 to a "direction" away from 0.
If you meant the former, then one unit of motion is one ratio, it can only grow or shrink compared to another ratio. Numerically it can have only the speeds of +(1Δ/1Δ) or -(1Δ/1Δ) and if it is not compared to another ratio, you cannot even determine its sign (or determine whether it is growing or shrinking).
Show me how you would make that determination without that comparison.
In RST, a unit of motion cannot have a different speed than ±(1Δ/1Δ). A change from unit speed expansion +(1Δ/1Δ) to unit speed shrinkage -(1Δ/1Δ) does not require a 0 speed.dbundy wrote: This, of course does not require crossing 0, but it should be understood in the sense of the reference to 0.
That's what the unit boundary is for. Speed discontinuities can occur there ...from +(1Δ/1Δ) to -(1Δ/1Δ)dbundy wrote: Otherwise, I can't see how we can progress (no pun intended).
That does not make sense because individual units of motion always move at unit speed ±(1Δ/1Δ). That's the Larson's Law !dbundy wrote: Changing signs requires changing "directions" and that requires crossing over unity (0), or using it as a reference.
It seems to me you have thrown that law out of the picture
Only the scalar "direction" can vary between units. I emphasize, that it can vary "between units" - not "within unit".
Re: Relativity of "Direction"
Oh man, we are not communicating well, and I don't know how to get a handle on it.
Let's try it again.
Let's try it again.
I think we both agree with him, right?Larson wrote:
We have found that the normal space-time progression involves n units of space for each n units of time, which means that the velocity of the progression, is always n/n or unity.
If I understand it correctly, you wouldn't agree to that statement completely, Is that fair to say?He went on to write:
In beginning an examination of the consequences of the two Fundamental Postulates we note first that they involve a progression of space/time which is similar to the progression of time as it is ordinarily visualized. Let us consider a location A somewhere in space-time. During the next unit of time this location progresses to A + 1 in time and since one unit of time, on the basis of the First Fundamental Postulate, is equivalent to one unit of space the location also progresses to A + 1 in space. When n units of time have elapsed the location has progressed to A + n both in space and in time.
Re: Relativity of "Direction"
That's because there is a mess with the units. We are interchangeably communicating about:dbundy wrote:Oh man, we are not communicating well, and I don't know how to get a handle on it.
1) Standalone magnitudes of space and time *.
2) Changes/deltas between magnitudes of space & time
3) Ratio of deltas (as defined in pt.2). a.k.a. Scalar speed
...a) Canonical scalar speed notations, e.g. +(1Δs/1Δt)
...b) Incomplete scalar speed notations, e.g. 1/1 or 1Δ/1Δ
...c) Ambiguous operational scalar speed notations, e.g. (0) = +(1Δs/1Δt) = -(1Δs/1Δt)
4) Changes/deltas between scalar speeds (as defined in pt.3), a.k.a speed deviations/displacements
I agree with both because he is talking about a special case which is this one.dbundy wrote: I think we both agree with him, right?
...
If I understand it correctly, you wouldn't agree to that statement completely, Is that fair to say?
When he is not taking about that special case, his words are more general and revealing:
...and the changeover from the positive speed +(1Δs/1Δt) to the negative speed -(1Δs/1Δt) occurs at the unit boundary. To have a reversal you need more than one unit of motion in order to have that boundary. The speed so generated is an average computed over multiple units. That speed is different for different observers (e.g. material and cosmic) because of their different "directional" normalizations, which are based on the identity +(1Δs/1Δt) = +1Δs/+1Δt = -1Δs/-1ΔtDB Larson in NBM pg.97 wrote: Since motion exists only in units, according to the postulates that define a universe of motion, and each unit of motion consists of one
unit of space in association with one unit of time, all motion takes place at unit speed, from the standpoint of the individual units. This speed may, however, be either positive or negative, ...
Do you dispute that identity?
* IMO such standalone magnitudes don't exist.
Re: Relativity of "Direction"
Horace wrote:
When he is not taking about that special case [unit motion], things become much clearer:
DB Larson in NBM pg.97 wrote:
Since motion exists only in units, according to the postulates that define a universe of motion, and each unit of motion consists of one
unit of space in association with one unit of time, all motion takes place at unit speed, from the standpoint of the individual units. This speed may, however, be either positive or negative, ...
Yes. I do dispute it. Polarity signs need not be associated with the speeds Larson is referring to. I think you have confused his meaning of negative (s/t) and positive (t/s) speeds. When the space oscillations occur, we get what we might call "less than unit space speeds," i.e. s/t = 1/n) and when time oscillations occur, we get what we might call "less than unit time speeds," i.e. t/s = 1/n,Horace wrote:
...and the changeover from the positive speed +(1Δs/1Δt) to the negative speed -(1Δs/1Δt) occurs at the unit boundary. To have a reversal you need more than one unit of motion in order to have that boundary. The speed so generated is an average computed over multiple units. That speed is different for different observers (e.g. material and cosmic) because of their different "directional" normalizations, which are based on the identity +(1Δs/1Δt) = +1Δs/+1Δt = -1Δs/-1Δt
Do you dispute that identity?
An earlier attempt of mine to capture the two perspectives in one chart is shown below. It's two views of the same thing, like the teeter-totter analogy. However, the space and time progression lines in the lower chart ought to be swapped, if we envision the familiar upper chart of the MS perspective being turned over at the origin, to attain the CS perspective, but you get the idea, I think:
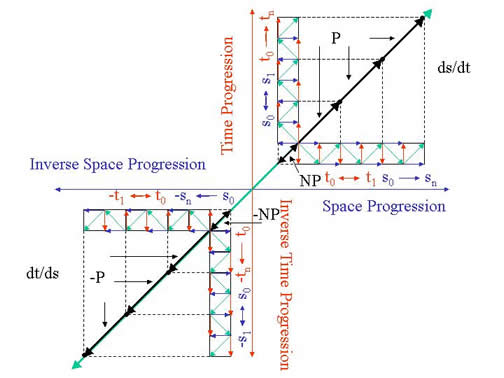
From the MS perspective, 1/n time speeds appear to be over-unity space speeds (s/t = n/1), and vice-versa, from the CS perspective, 1/n space speeds appear to be over-unity time speeds (t/s = n/1).
However, Larson would never write over unity speeds as such, since time has no direction in space, and space has no direction in time. Crossing the unit speed boundary, s/t speeds become t/s speeds, with unity being the maximum speed attainable in both cases, because changes of locations in space (time) must become changes of location of time (space) at that point.
It's as straightforward as that. Normalization has nothing to do with it, as far as I can see.
Re: Relativity of "Direction"
Evidently you cannot dispute it on mathematical basis, nor on "appeal to authority" basis, so that leaves you with logical and conceptual basis, which I prefer anyway.dbundy wrote: Yes. I do dispute it.
DB Larson in NBM pg.97 wrote: Since motion exists only in units, according to the postulates that define a universe of motion, and each unit of motion consists of one
unit of space in association with one unit of time, all motion takes place at unit speed, from the standpoint of the individual units. This speed may, however, be either positive or negative, ...
The signs are needed in the canonical scalar speed notation in order to avoid the "directional" ambiguity. How else would you distinguish inward from outward unit scalar speeds? This is manifested in that passage above, written by Larson, where he is analyzing only the attributes of unit scalar speed - not any speed deviated from unity. He was the one to use the words "negative" and "positive" in reference to unit scalar speed that he was expressing in the canonical form of 1Δs/1Δt , as evidenced by his words "each unit of motion consists of one unit of space in association with one unit of time...".dbundy wrote: Polarity signs need not be associated with the speeds Larson is referring to.
Not according to Larson. In that passage above he was considering unit speed only (not any deviated speed). Exchanging the numerator with the denominator does not affect the unit speed, thus your distinction between (s/t) and (t/s) does not make sense for the unit speed that Larson was considering.dbundy wrote: I think you have confused his meaning of negative (s/t) and positive (t/s) speeds.
That might be true in general when using the operational notation of a fraction, but Larson was not using that notation and he was writing only about unit speed in that passage above.dbundy wrote: When the space oscillations occur, we get what we might call "less than unit space speeds," i.e. s/t = 1/n) and when time oscillations occur, we get what we might call "less than unit time speeds," i.e. t/s = 1/n,
Re: Relativity of "Direction"
For those that are quietly following this thread, the operational notation of rational numbers, that Doug is often referring to, is depicted below the number line on the following diagram:
In RST, the unit speed would be written as zero in operational form.