Doug,
Could you introduce the LRC for first time visitors:
1) What it is and how it came to be
2) How is it different from Dewy Larson's Reciprocal system and RS2
3) What are its strengths, weaknesses, opportunities and threats.
LRC Introduction
Moderator: dbundy
Re: LRC Introduction
The full name of the LRC is the Dewey B. Larson Memorial Research Center. It is an incorporated non-profit organization, with 501(3c) tax exemption status.
It was formed, when the late Mr. Jesse Greer, of Kentucky, encouraged it and donated the funds for it.
The research we wanted to pursue was based on my discovery of the work of Stephen Wolfram with what was known as "cellular automata." The first big breakthrough was the development of the Progression Algorithm (PA), which was adopted from rule 254 in Stephen Wolfram’s list of cellular automata rules.

For him, it was the most uninteresting of all 256 rules. However, by reinterpreting the progression of space and time in this rule, in order to incorporate them as two, reciprocal, aspects of motion, we were able, for the first time, to graph the scalar progression and the “direction” reversals, which enabled us to visualize the meaning of these concepts and think about their implications in terms of numbers.
At the time, we dubbed the work as the Net-Zero Project, and it has grown from there. The net-zero label referred to the fact that the PA algorithm showed the zero progress of one aspect or the other of the uniform progression.
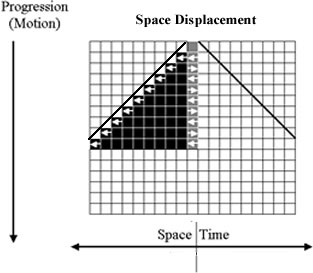
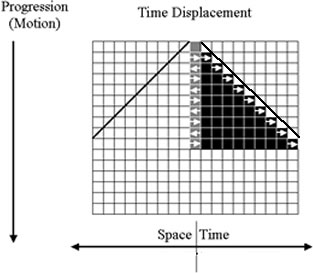
From this, it soon became apparent that only two space|time ratios were possible, 1|2 and 2|1, and that these had to be combined to get anything interesting, but combining them only led us back to the unit progression, 1|1! However, we eventually recognized that the sum of the numbers 1|2 and 2|1 was actually the sum of 2|2 and 2|2 in terms of total units of progression; that is, there is one unit of inward motion, for every unit of outward motion, in a cycle of two “direction” reversals. Hence, the complete equation for summing two, reciprocal, units of scalar space|time oscillation had to be
ds|dt = 1|2 + 1|1 + 2|1 = 4|4 num,
where num is an acronym for “natural units of motion.”
At first, the idea was to form the LRC as part of ISUS, to fund various RST-based research projects, but disagreements as to the ground rules eventually led to my decision as ISUS President to resign and establish the LRC, as an independent organization.
I've written more, by way of introduction here: viewtopic.php?f=17&t=430
It was formed, when the late Mr. Jesse Greer, of Kentucky, encouraged it and donated the funds for it.
The research we wanted to pursue was based on my discovery of the work of Stephen Wolfram with what was known as "cellular automata." The first big breakthrough was the development of the Progression Algorithm (PA), which was adopted from rule 254 in Stephen Wolfram’s list of cellular automata rules.

For him, it was the most uninteresting of all 256 rules. However, by reinterpreting the progression of space and time in this rule, in order to incorporate them as two, reciprocal, aspects of motion, we were able, for the first time, to graph the scalar progression and the “direction” reversals, which enabled us to visualize the meaning of these concepts and think about their implications in terms of numbers.
At the time, we dubbed the work as the Net-Zero Project, and it has grown from there. The net-zero label referred to the fact that the PA algorithm showed the zero progress of one aspect or the other of the uniform progression.


From this, it soon became apparent that only two space|time ratios were possible, 1|2 and 2|1, and that these had to be combined to get anything interesting, but combining them only led us back to the unit progression, 1|1! However, we eventually recognized that the sum of the numbers 1|2 and 2|1 was actually the sum of 2|2 and 2|2 in terms of total units of progression; that is, there is one unit of inward motion, for every unit of outward motion, in a cycle of two “direction” reversals. Hence, the complete equation for summing two, reciprocal, units of scalar space|time oscillation had to be
ds|dt = 1|2 + 1|1 + 2|1 = 4|4 num,
where num is an acronym for “natural units of motion.”
At first, the idea was to form the LRC as part of ISUS, to fund various RST-based research projects, but disagreements as to the ground rules eventually led to my decision as ISUS President to resign and establish the LRC, as an independent organization.
I've written more, by way of introduction here: viewtopic.php?f=17&t=430
Re: LRC Introduction
I noticed, that you summarized this entire graph with one ratio: 1|2 and that ratio is your shorthand symbol for the average speed, which deviates from unity on this graph.dbundy wrote:
That shorthand symbol can be expanded to enumerate the progression of individual aspects of that motion, creating an infinite series like this:
+1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, ...
( this graph had 10 rows so this series has 10 members listed as well, but it could've been continued ad infinitum )
Do you agree?
Re: LRC Introduction
Why wouldn't this be possible as well ?dbundy wrote: From this, it soon became apparent that only two space|time ratios were possible, 1|2 and 2|1, ...
Re: LRC Introduction
Yes. That's when I made the chart to show it more clearly, but I didn't understand it completely and put the wrong PAs in it at the top right:I noticed, that you summarized this entire graph with one ratio: 1|2 and that ratio is your shorthand symbol for the average speed, which deviates from unity on this graph.
That shorthand symbol can be expanded to enumerate the progression of individual aspects of that motion, creating an infinite series like this:
-1s/+1t, +1s/+1t, -1s/+1t, +1s/+1t, -1s/+1t, +1s/+1t, -1s/+1t, +1s/+1t, -1s/+1t, +1s/+1t, -1s/+1t, ...
( this graph had 10 rows so this series has 10 members listed as well, but it could've been continued ad infinitum )
Do you agree?
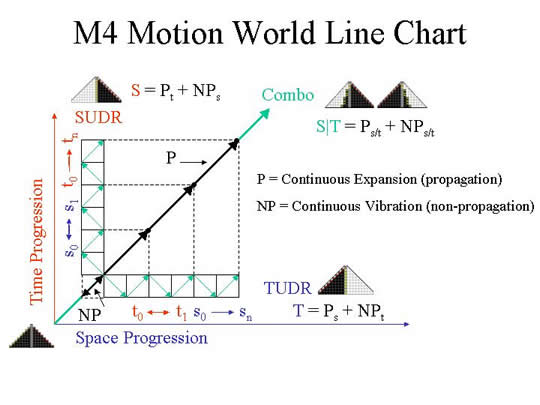
To answer your question, why I don't think it's possible, I can only refer you to Larson's explanation, which I confess is not all that clear to me, but I chose to take his word for it. Now, I can develop the consequences of simple harmonic motion, but I wouldn't be able to do so, if it were not harmonic. Also, everything in nature seems to be harmonic - waves in water, tunning forks, bells, whistles, pendulums, etc.
From Chapter 4 of NBM, Larson wrote:
Another possibility is simple harmonic motion, in which the scalar direction of movement reverses at each end of a unit of space, or time. In such motion, each unit of space is associated with a unit of time, as in unidirectional translational motion, but in the context of a stationary three-dimensional spatial reference system the motion oscillates back and forth over a single unit of space (or time) for a certain period of time (or space).
At first glance, it might appear that the reversals of scalar direction at each end of the basic unit are inadmissible in view of the absence of any mechanism for accomplishing a reversal. However, the changes of scalar direction in simple harmonic motion are actually continuous and uniform, as can be seen from the fact that such motion is a projection of circular motion on a diameter. The net effective speed varies continuously and uniformly from +1 at the midpoint of the forward movement to zero at the positive end of the path of motion, and then to -1 at the midpoint of the reverse movement and zero at the negative end of the path. The continuity and uniformity requirements are met both by a continuous, uniform change of direction, and by a continuous, uniform change of magnitude.
Re: LRC Introduction
Note that the series listed above was written in a differential form.dbundy wrote:YesHorace wrote:... an infinite series like t this:
+1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, +1Δs/+1Δt, -1Δs/+1Δt, ...
Do you agree?
If this series is written in absolute form ( where the numbers denote the absolute magnitude of space and time, as measured from the ORIGIN OF THE GRAPH - marked in red color ) then it would appear as this:
0s/0t, 1s/1t, 0s/2t, 1s/3t, 0s/4t, 1s/5t, 0s/6t, 1s/7t, 0s/8t, 1s/9t, 0s/10t, ...
I emphasize that this is true on that GRAPH and does not have to be true in another system.
Do you agree?
Re: LRC Introduction
Yes. I think so - but I would have to see the other system you are referring to in order to say for sure.
Re: LRC Introduction
THE OTHER SYSTEM does not matter for now. I wrote this only to emphasize that my statements referred to that GRAPH only.
BTW: I added the delta characters to this post.
BTW: I added the delta characters to this post.
Re: LRC Introduction
I'd like to make a correction to the origin of the graph (marked in red color) in this post because the origin there was drawn in the middle of the unit on the horizontal axis.
That origin mark introduced a conceptual error which caused the pyramid of the PA to possess a single block at its apex.
While that looked pleasingly graphically it carried with itself the misleading implication, that space and time shared the same unit at the apex.
It was not clear whether that was a unit of space or unit of time, it was kind of a "shared unit" with an unavoidably shared direction.
We know this to be wrong because space does not have a direction in time and vice versa.
The lack of directional arrows in the apex block, underscores this incoherency in that graph.
So below is a corrected graph of the same motion and it does not have a shared apex: Note, that this alteration divides the graph into the left (gray) side that depicts space and the right (black) side that depicts time.
These two sides have no shared apex, no shared column in the middle no oriented st axes and are essentially two separate graphs.
Both, the time and space, can change in any "direction" (outward, inward) so there would appear to be a total independence between them if not for the synchronization along the vertical (progression) axis.
If not for that synchronization, it would be a 3 dimensional graph. (not to be confused with 3D space or time).
I write "3 dimensional" because it could be described by 3 independent variables on the space axis, time axis and progression axis; despite that the time and space axes are not perpendicular to each other on that graph.
But even with the latter alteration, we can already give the left and right halves separate origins (red) and separate axes, like this: From there it is not far to separate the space and time axes even more, even up to a point of making them perpendicular to each other ( like you started to do here ) or putting them in separate graphs altogether, as long as some auxiliary device maintains step-by-step correlation between them to depict the progression.
That origin mark introduced a conceptual error which caused the pyramid of the PA to possess a single block at its apex.
While that looked pleasingly graphically it carried with itself the misleading implication, that space and time shared the same unit at the apex.
It was not clear whether that was a unit of space or unit of time, it was kind of a "shared unit" with an unavoidably shared direction.
We know this to be wrong because space does not have a direction in time and vice versa.
The lack of directional arrows in the apex block, underscores this incoherency in that graph.
So below is a corrected graph of the same motion and it does not have a shared apex: Note, that this alteration divides the graph into the left (gray) side that depicts space and the right (black) side that depicts time.
These two sides have no shared apex, no shared column in the middle no oriented st axes and are essentially two separate graphs.
Both, the time and space, can change in any "direction" (outward, inward) so there would appear to be a total independence between them if not for the synchronization along the vertical (progression) axis.
If not for that synchronization, it would be a 3 dimensional graph. (not to be confused with 3D space or time).
I write "3 dimensional" because it could be described by 3 independent variables on the space axis, time axis and progression axis; despite that the time and space axes are not perpendicular to each other on that graph.
But even with the latter alteration, we can already give the left and right halves separate origins (red) and separate axes, like this: From there it is not far to separate the space and time axes even more, even up to a point of making them perpendicular to each other ( like you started to do here ) or putting them in separate graphs altogether, as long as some auxiliary device maintains step-by-step correlation between them to depict the progression.