It was brought to my attention that Miles Mathis (as recently as April 10, 2020) released a paper entitled 'Squaring the Circle' as a 'part 2' follow-up to an existing paper from 2006. The concerned paper can be found here: http://milesmathis.com/square2.pdf
What follows is an annotation of any/all relevant content (as deemed of practical need/use)
as it relates to both: "squaring the circle" and the relationship between Φ and π² as "yang-space" and "yin-time"
or in other words: "yanging the yin" being my parallel to Miles' "squaring the circle".
As a preface: I respect the work of Miles Mathis because his approach is rooted in a discipline in ever-endeavoring
to find the very root of a problem(s) by way of conscious inquiry. I appreciate such an approach, and thus take
the opportunity to draw from both inspired and inspiring work while reflecting it in light of RSoT
and its recent uncovering of 1=Φπ²/16.
Miles clearly acknowledges the need for a π of 4 in kinematic situations, which happens to be thus a "fixed" integral in a universe of motion such as our own. What should follow from this is π is always related to the rational integer '4' if/when dealing with any/all real-world physics, from cosmology to molecular biology. To say π simply equals '4' is not enough, however: it needs to be reflected somewhere in/as some relationship between our space s on time t universe. If we let v be velocity, v=s/t must accommodate a '4' somewhere in that as a fixed "root" of kinematic motion. This will turn out to be 4/√Φ as we shall find shortly.I thought of something last night. Don't know why, since I wrote part 1 on this problem way back in 2006. I thought to ask myself how my replacing of pi with 4 would affect this problem. The short answer is: it wouldn't, necessarily, since the historical problem had to do with the area of drawn circle. My pi papers don't affect area, since area is not kinematic.
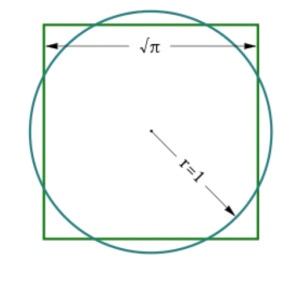
My own reflection to the capping question is: it's not that those who came before us didn't know how to measure... it's more-so they did not know what to measure. Understanding how the line (or mascu-line if I may) may relate to the curve (or femin-ine as I would) is not indifferent to understanding how the square relates to the circle thus their union would involve finding the pre-projective properties of a square to be the same with/as a "corresponding" circle: the same endeavor of Miles' paper, the same is mine (albeit from a different approach) and the same is ultimately reflected in 1=Φπ²/16 as corollary of π=4/√Φ.But then it occurred to me to ask myself why the historical problem was one of matching the area of a square to a circle, instead of matching the circumference of a square to a circle. That would be an equally interesting problem of construction, one that historically would also include pi. Instead of r²π=s², we would have 2rπ=4s. So a square of side 1 would be matched by a circle of r=2/π. Or a circle of radius 1 would be matched by a square of side π/2. So why was this question always in the form of area?
It can thus be said of this π: from Φ's own rib is derived π. This is no "accident" of nature: that humanity has been in dark times for many thousands of years by rather religiously dividing (mathematicians included) is a problem this equality is equipped to promptly address. Therefor this annotation is not only intended to highlight Mathis' strengths, but his barriers to making a true and lasting difference that his work would otherwise merit - his inductive discipline is not something a typical dogmatic Relativist can possess, as the very possessing of it would have lead them to the very same questions Miles has already posited, addressed, uncovered the root(s) of, and made corrections wherever necessary. This is exactly what the enterprise of science ought to be, but is not presently.
As to whether or not one is even able to derive an "ought" from an "is", one can certainly derive an ought not from an unfortunately is, the distinction being the latter actually mandates one acknowledge what is to-begin-with, before being able to improve upon. This involves knowing what is not necessarily true, else progression "relatively" and temporarily ceases and time takes her curve accordingly. It is the intention of the author to contribute to the understanding of both how and why this is so, as time is merely a measure.
"Of what"? is the problem... nobody seems to know what to measure.
They do not have the same area because a square and a circle are hardly in/of the same dimension, thus the "circumference" of a square is not the same as the circumference of a circle, especially in the context of a universe of motion wherein scalar and non-scalar motion are each unique kinds of motion. We need an alternative way of relating the two which may capture what is commonly shared between the circle and the square.Also curious is that a square and circle of equal circumference do not have the same areas. A square of side 2 has an area of 4, while an equivalent circle has an area of 16/π, or about 5.1. So if you want to create the maximum area, a circle is the way to go. That helps us understand the orbit, which tends over time to seek the circle. We have seen many other explanations for why it tends to do that, but we have never been told the central reason: charge. We have been told the circle is mathematically and kinetically the most efficient shape for an orbit, which is true, but the circle is also the most efficient as a matter of charge. All celestial bodies are charge engines, as I have proven. Therefore, if that engine wishes to maximize the amount of charge it can capture from a central body, it will move about that body in a shape that encloses the area of most emitted charge: the circle.
Miles' question is certainly better than the area-approach (the bizarre "misdirection" matter aside). Perhaps it is more along the lines of "misconception" - that "squaring the circle" should have ever meant finding equivalent "area" indicates the same: not knowing "what" to measure. Squaring the circle should imply what we are after: establishing a relationship between the two. However, associating a radius to/with a square is highly problematic, and indicative of a misconception. To be fair: basically all of Western science is making this same error in conception because they do not see the impetus of motion (let alone motion itself as being the sole constituency of the universe) as being of variable two-fold nature: a rational terminating integer with a fixed (ie. "scalar") magnitude and a non-terminating irrational. Whereas integers are resolutely fixed to a magnitude (thus are technically their own squares), irrationals change according to a square. What is important is to find a way that these two become as one: one works with/off the other, and vice versa. This is the essence and basis of reciprocity, with the "square" and the "root" operations being a bi-directional terminus....
But back to our first question. Why not square the circle as a matter of circumference? Why talk of area? Given what I have discovered, I now think it was a matter of misdirection. If this question had been framed as a matter of circumference rather than area, someone might have figured out earlier what I did. Construction with real tools tends to push a person to a step method when comparing the circumference of a circle to a square, and that step method takes one to a manhattan metric or taxicab geometry, where pi=4. By that method, the equivalent square is easy to draw.
v = s³/t ↔ (st)² ↔ t³/s = e
s³/t ↔ (-8+8√5) ↔ t³/s
t³/s ↔ (+8-8√5) ↔ s³/t
"...as a matter of kinematics it has the same circumference as the circle" is problematic. The equivalence in/of the "circumference" is only apparent if/when projected (as in the case with a picture, for example). No such equivalence exists between a straight-line square (?) and a perfect circle (??) in a motion-based universe for the same reason above: a square and a circle imply two different dimensions - namely, rational and irrational. In order to understand this, it involves tackling (and perhaps conquering) a problem at the heart of number theory itself: the relationship between real and imaginary numbers (ie. complex analysis). Fortunately, Mr. Larson's intuition to "begin with unity" brings light to-the-forefront (and some much needed light at that). By way of taking the same approach we take the square of 1 such to concern unity and/or not:The square has a much larger area, but as a matter of kinematics it has the same circumference as the circle. Both circumferences are 8r. That is to say, if you treat the circumference as a distance that has to be traveled by a real body, the distances are equal. It will take the same time to travel the circle as the square.
1 = nº and/or Φ²-Φ
√1 = (root of) Unity as +1, -1
√+1 = 1
√-1 = i
_______________________
+1 = Unity (wherein s/t = 1)
-1 = Not Unity (wherein s/t ≠ 1)
-(-1) = Not Not Unity = Unity
(multiplicative reciprocity)
(s/t ≠ 1)Not-∞+Unity(s/t = 1)
We know √1 is therefor bound to "two" discernible and discrete conditions: unity and not (ie. anything and everything but). Inquire rationally: where does '1' even come from? What is the 'constituency' of '1'? Where, if anywhere, in the number system, using ordinary mathematics do we naturally see a discernible and discrete '1' emerge as a natural "product of a square?" What about in the irrational numbers? These strange numbers which do not terminate unless a local "approximation" is made... how does one rationalize irrationals? Is there a relationship between rationals and irrationals that exists naturally? I found these to be very important questions, as certainly there is such a relationship that exists.
The key is hidden as the solution to f(x) = x² - x - 1 set to naught, which we refer to as Φ, the golden ratio, and not only does it produce a natural '1' if/when squared, it "re"-produces itself along with it viz. Φ² = Φ + 1, or in other words: an irrational acts on itself to produce itself plus a rational and discrete '1'. How has this unique property been overlooked for so long, especially given the implied x² - x = 1 such to resolve into our discrete and rational integer 1, the root of which may (or may not!) concern unity? Yet a simple operator switch Φ² + Φ = (√5+2) yielding simply Φ³ merely makes the addition of an irrational non-unity (ie. 2, a duality) to the same irrational √5. Wait a minute... may we just be looking at the same "operation" from two different perspectives here? Is this not the same "operation" made in reverse?
"Powers of Phi":
±1 = Unity+∞-Not
Φ = (√5+1)/2 = (π+π√5)/2π = 1.618...
Φ² = (√5+3)/2 = (3π+π√5)/2π = (Φ+1) or 2.618...
Φ³ = (√5+2) = (4π+2π√5π)/2π = 4.236...
____________________________________________
-Φ³ + Φ² + Φ ± 1 = +1, -1
and
Φ² ± Φ = 1, Φ³
Combining the operators as a single expression, Φ² ± Φ = 1, Φ³ further yields a rational '1' in one direction, yet an irrational '4.236...' in another. This is an extremely important "junction" therefor, because it pins the R.H.S. to either a rational and discrete '1' or an irrational and non-terminating 4.236... based on a mere operator "switch"... a needed key in "yanging the yin" while highlighting the explicit need to measure the circle whose diameter is √5. The diagonal about a 2x1 rectangle is √5, thus a circle whose diameter is √5 both implicitly and explicitly concerns the diagonal about a 2x1 rectangle, or two unit squares side-by-side. √5 thus becomes instrumental in relating the line to the curve.
However note that it can be constructed "geometrically" from the level of the axes/plane itself up: rational and discrete (ie. "geometric") axis x and irrational and imaginary (ie. "complex") axis i. This complex plane "works" in kinematics for a reason, if even present-day science doesn't understand the "nature" of it: that's just how it is in nature: image and likeness, yang and yin, space and time, line and curve etc. So how do they actually come together? How do we "yang the yin" and/or "square the circle"?No one ever thought to frame this question as one of kinematics or motion, however. It was framed as geometric only, which served to bury my discovery for millennia. And the fact that it was framed as geometric from the beginning messed up kinematics all along, because mathematicians and physicists never figured out that kinematics couldn't be expressed by classical geometry. They never understood that motion added a degree of freedom as well as a mathematical dimension. In other words, they didn't understand how a circle was actually constructed. Although in geometry the circle is given, in the real world a circle can't be given. It has to be constructed.
Miles was/is off by miles with his trying "area is not kinematic" as it certainly is, the oversight owing to the broad constituency of what is to follow, especially relating to the need to measure for π only by way of the circle whose diameter is √5.You will say that if that circle and square are actually equivalent regarding circumference, then it is the square that maximizes the area, not the circle. So the planets should orbit in squares to maximize charge intake.
Yes, it does get confusing, I admit. But the answer is that area is not kinematic, as I already admitted.Area really is static or geometric, since we don't care how long it takes a real body to surround that area or shape. Area is a function of content, not motion. So in that case we don't use the equivalency above, which is a kinematic equivalency. In the case of charge, we want to know how much charge is in that area, so even if we bring time into the problem, it doesn't make it kinematic Say we want to know how much charge is in a given area in one second. Well, we don't track individual photons, do we? We don't care how fast they are going, except insofar as it tells us whether they are in or out during that period. So the above square and circle aren't equivalent in that sense.
Say a universe abides in/as one primary conjugate magnitude according to the "square" operation √1. The progression being as +1 is the vehicle of light (ie. "speed" of, though this author rejects the treatment of light itself as even having/being a "velocity"), and its own conjugate being gravitation as -1. We only need a simple axes a universe of motion may concern, given our equation is a simple v = s/t for velocity and/or the reciprocal e = t/s for energy wherein s/t x t/s = 1. This should be very easy to do as yet again corollary of Larson's intuition to "begin with unity" thus immediately concerns photons (ie. light) as carried by the progression, which we may recall is functionally a constant 1 as could be in counter-operation to a constant -1, hence v and/or e implicitly/explicitly and ultimately concerns the "roots of unity".
We need an axes that may capture this "constant" progression/gravitation condition such to capture any/all particulars (ie. matter, or M in Einstein's e=MC²) which are displaced from unity. We may express this binary of conditions as any particular(s) "particles" as measured either s/t ≠ 1 (thus as some displacement(s) from unity) or in the case of light s/t = 1( thus no displacement(s)). If the former, we are dealing with a particular displacement(s) from unity. If the latter, we are both implicitly and explicitly concerning unity... or not, depending on if there is an "outstanding" root operation on the 1 such to potentially measure a gravitational magnitude -1 rather than a progressive one +1. It is important to understand that what applies to space and time themselves must also apply to all motion-based everything, as according to RSoT: there is only motion, thus the RSoT has already intuited the need for a "quantum" π of 4 long before their finding of the connection to Φ.
What the correction of π to 4/√Φ does is it effectively re-couples the "quantum" 4 to its actual measure, instead of the "approximated" 3.14159... and "transcendental" only for transcending the grasp of present-day "science". By way of satisfying the condition that one 'rational' 4 is in a fixed relation with one irrational root of Φ, the coupling of the rational/irrational numbers (thus the real/imaginary complex analysis) may occur, and does occur, and naturally.
In reality, the "complex analysis" is actually not complex, it is merely the cooperation of rational and irrational numbers.
What Miles is describing here is s/t=1 or simply the progression, and understandably (still, bizarrely) claims the unit square s = 1 has a larger "average radius" than an associated 2r = 1 circle. Squares do not actually have a radius. A radius is a property of a circle, not a square. Yes, we are looking to unite the two, but saying the square has a radius is like saying yin has her own wang, leaving yang... hanging.To see that, we have to imagine we are one of the photons. Say all photons are released from the center of the area and travel out on a radial line, as if they are coming out from a central sun, for instance. They don't see the red square above as equivalent, since it has a much larger average radius than the circle. So they would see the equivalent square as the one that had the same average radius as the circle. That would be the first equivalency we studied above, of static perimeter. Given that equivalency, we then find the circle has the maximum area.
It certainly can be if/when the universe employs a multiplicative/square function by default, such as to give rise to a scalar magnitude(s) upon which rests rotating bases of time. 2π/2π would then describe 1 such discrete unit of time and/or user-defined measure of time. (π+π√5)/2π is thus significant should it turn out to be the case that 4/√Φ = π implies 16/Φ = π² being in any relation to Einstein's e=MC², which happens to be the case.But why? Why does the circle have more area that the equivalent square? If the average radius of both figures is the same, why would one have more area than the other? Shouldn't the same average radius give us the same area? No, because area isn't a function of radius alone.
...not all radii need be averaged, they may be fixed/scalar as in the 2r = 1 such to concern a unit square, noting that √5 is simply a diagonal about two conjoined unit squares...That is why area doesn't follow circumference, as we saw in previous papers. Area is a function of shape, and shape can't be determined by average radius. You can create an infinite number of possible shapes with the same average radius,
...hence the use of the fixed/scalar (and invariably scalable) Kepler triangle such to concern each: 1, √Φ, Φ.but they won't have the same areas. This is because shape is determined by average radius and the angle to radial line. The circle maximizes that summed angle, since each and every value in the sum is 90. With the square, only four values in the sum are 90, while all others are less. If we compare the square to the equivalent circle, we find the square loses area more often than it gains, due to those angles.
This is the same triangle upon which the Giza pyramid was constructed by the way, by way of use with:
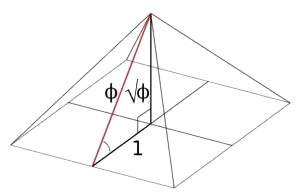
Noting how the plateau is constructed with the "Powers of Phi" explicitly concerned:
And the "golden" axes depicted here which relates to the '4' in/of 4/√Φ is a big way (to follow):
__________________________________________________________________________
Credit (images): Gary Meisner and/or https://www.goldennumber.net/great-pyra ... den-ratio/
You can measure a square using a radius, but the radius of the circle concerning that same square must be half that of the square. For example, measuring the square with a side of 1 concerns the circle r = 1/2 and/or 2r = 1. This is because, once again, a square and a circle are not technically in the same dimension, as squares do not have a "variable radius", let alone a radius. The best one can do is using the same square and circle, the diameter of the circle described by 2r = 1 will only meet the "circumference" of the square (I prefer perimeter here) in four places both symmetrically and equidistantly, as with a "cross" depicted both in the preceding Giza plateau overhead and what is to follow, as it constructs the axes we need to "yang the yin".Also notice that when the angle to radius is maximized with the square, the length of the radius is minimized. So when the square is most like the circle, it has the least radius. So the angle being at maximum doesn't really help it.
In other words, you just have to think of the square as a type of circle, and try to measure it using a radius, instead of with external legs. The square then becomes a circle with a variable radius, right? Its radius has four maxima and four minima. You then compare it to the circle in that way.
This is needlessly complicated. However, while we are here we might as well point out the two most important points: the angle is always 90 with the circle (electricity and magnetism share in this relationship, thus is integral to space and time) and only four places with the square. We are getting closer to the '4' about the golden root.The next step is to let the radius of the square intersect its own perimeter, then notice that an angle is created. While that angle is always 90 with the circle, with the square it is 90 only at four places—the midpoints of the legs. At all other points that angle is less than 90.
The problem can not be solved in this way at all, because the concerned circle is not one whose diameter is √5. In RSoT, the space/time ratio is 1/1 if/when concerning a photon. Again, s/t x t/s = 1, thus we merely only concern ourselves with the circle whose property(s) is (are) shared with a square. Miles intuited this relationship a long time ago: that π is "equal to 4.00". His outstanding oversight is missing the imperative to fix this discrete '4' about a base of motion. This roots into the real matter of the problem: Miles seems to deny and/or disregard the imperative that we recognize our universe as a "kinematic universe" such that virtually the only property it relies on is the very same "kinematic" π = 4 property Miles uncovered, yet catastrophically fails to apply it: for we live in a UNIVERSE OF MOTION. By acknowledging this fact, we may let all motion according to s/t ≠ 1 concern all motion s/t = 1 wherein 2π serves as a variable rotating base such to be divided into halves/quarters etc. as needed given the desired measurement/juxtaposition(s) to be taken.
That square and circle have equal areas, and that is because the square loses the same as it gains, due to angles to radius. But that square and circle do not have equal perimeters. The circumference of the circle is 2pi=6.28, while the circumference of the square is 4√pi=7.09. The square needs a larger perimeter to create an equal area. If we make the square smaller to match the perimeters, those four external areas in the corner get smaller, while the four external areas of the circle get larger. So the angles gained by the square become smaller than the angles lost, and the summed angle to radius therefore becomes smaller with the square. So all you need to know here is the radius and the angle to radius. The problem can be solved with that and only that.
There should be no summing anything, certainly not of angles, except how many times the circle kisses the square.You will say that summing the angle of the square won't help us, because the angle is over 90 exactly as much as it is under 90, so as a sum it will even out to 90, just like the circle. But you see that you can't ever let it go over 90. Any angle that is not 90 will cause the square to lose area compared to the equivalent circle, because that angle causes a cut into the interior of the perimeter. You will say that angle also causes a gain on the other side of the radius, but that gain is outside the tangent, so it doesn't count toward area. That angle is part of the next differential. We are only following angles on the short side here. So in summing the angle, you don't measure from the same direction as you go around the clock. You measure from whatever direction will give you an angle under 90. I trust you followed that logic.
There is thus no rationale (both practical and rhetorical) and/or logic in attempting a squaring of a circle
whose diameter is not the needed √5... the same corresponds to the diagonal of two unit squares side-by-side
thus is able to capture dichotomy: a rationing of two. In both Miles' case, the "Squaring the Circle", and in mine,
a "Yanging the Yin" which, as I hope to tacitly show, are the same exercise.
...Miles basically closes with this, before citing a number of other... not-as-good answers to the problem along with:That is the simplest answer*, and it still requires some precise visualization, but I find it very much preferable to the answer you will find on the internet.
Despite Miles not actually "Squaring the Circle" as intended, he did not even utilize the '4' he foundAnd so on down the line. I found no one that gave you my simple answer. Is it because they don't know, or is it because they aren't good at simplifying an explanation down to basics?
to construct/show any symmetry between the square and the circle. Wasn't that the point?
We started off okay, (we ourselves arrived at the point of needing to construct an axes that allows for
the capturing of any/all s/t≠1 motions in relation to s/t=1) then Miles asked us to imagine being a photon
and started talking about the "average radius" of a square. Let's pick up with the axes.
We may begin towards constructing the symmetrical axes needed here,
first drawing attention back to the "Powers of Phi" relationships:
±1 = Unity+∞-Not
Φ = (√5+1)/2
Φ² = (√5+3)/2
Φ³ = (√5+2)
and seeking/finding what is common/shared among all three powers in relation to unity: √5.
Or in other words: whereas another said "make the two as one" I take it one step further and say "make the three as one".
In doing so, all "square" operations involving √5 implicitly concerns the relationships noted above.
What does it even mean to "square" anything?
Does it not take a square to multiply a thing by itself?
How can area (ie. "content" of a square) thus be said to be non-kinematic,
esp. if gravitation can be shown to be a function of radius alone?
If π-based Φ can be written in terms of π as (π+π√5) / 2π
and/or even by "square rooting the circle" as √(2π(π√5 + 3π)) / 2π
why can not π be written in terms of Φ? If it can,
then √5 can act as a "coupling constant" between them,
recalling √5 is any diagonal between the corners of
two "unit squares".
All content is motion, as motion is (as postulated in RSoT) the sole constituency of the universe.
All real-world physics thus concerns a "kinematic" π by default, as space and time are already coupled
via naturally being multiplicative reciprocal aspects of MOTION, the very thing
the "kinematic" π concerns. The only "terminal" between the two that is needed is a "square" operation
in two directions, "inward" or inverse square as in √16→4, and "outwards" or ... outverse (normal) square 4²→16.
This bi-directional {n1/2 ↔ n2} squaring is extremely important given the relationship space and time have:
→ v = s³/t ↔ (st)² ↔ t³/s = e ←
_________________________
v = s³/t (3D space on 1D time)
e = t³/s (3D time on 1D space)
It is for this reason we must measure the circle whose diameter is √5
such to derive a valid coupling between the two to "yang the yin"
and/or "square the circle", noting use of the "Kepler triangle"
whose proportions are 1 x √ Φ x Φ or one rational unit,
one irrational number, and a square of the latter:
Beginning with a circle whose diameter is √5,
place two unit squares inside the circle side-by-side
(either horizontally or vertically, the latter is shown)
and find √5 as the diagonal between any two opposite corners (AB shown)
noting this diagonal as being equal to the diameter of the circle.
Add 1 unit distance to this diagonal (√5 + 1 as AC) and find the mid-point (/2 as D).
Note: by way of rotating the √5 diagonal AC about the origin,
the midpoint D coincides with the circle whose diameter is 2r = 1
and "kisses" the unit square four times equidistantly, thus a more precise π
can be retrieved directly from Φ expressed as a ratio of Φ.
This ratio is 4/√Φ = π.
...demonstrating a conjoined "scalable" coupling found naturally via equidistant rotations of the associated Φ spiral. The need to measure the √5 circle relates to the "squaring" of Φ (which can also be generalized as (π+π√5)/2π or "Φ in terms of π"). What is crucial to note is if/when "squaring" this π-based Φ, one finds (3π+π√5)/2π which is a difference of... exactly 2π, such to concern one rotation and satisfies our 2r = 1. In other words: Φ² = Φ + 2π/2π or one full rotation of/as a photon. If allowing 2π to describe any rotating base, the denominator implies "per rotation of 2π" which can thus apply to any variable constituency(s) of the numerator, recalling space and time are multiplicative reciprocal aspects of motion. In all practicality, √5 is thus in every sense as integral to motion as it is to Φ, because it will soon be shown that Φ is actually a constituency of an even more important relationship (to follow) that "illuminates" and/or "sheds light on" Einstein's e=MC² which certainly "yangs the yin".
With π corrected to 4/√Φ, we can now observe the crucial junction-function of which the former is a (real) root of:
f(x)= x⁴ + 16x² - 256
roots (zeros):
x= ±√9.88854381999...
x= ±i√25.88854381999...
____________________________________
wherein x=4 and x=4i yields +256 and -256 respectively
viz. a "coupling" between real/imaginary resting on the integer '4'
cooperatively concerning a relative ± 256 or "spread" of 512.
as having an important symmetry about the real/imaginary axes described by the roots of the above function. This axes is composed of half 'real' and half 'imaginary' elements, thus for any/every relationship between rational 'discrete' units and irrational 'non-terminating' magnitudes (such to describe a universe of motion) the real element is always 1/2. This is true by Ananke (necessity) owing to the properties/constituency of the axes itself incessantly "rationalizing" rational/irrational, as in the case of 4/√Φ and/or 16/Φ if squared. The square as 16/Φ (or real element x² as 9.888...) is interesting because it can simply be substituted into/as the C² term in/of Relativity's e=MC²:
π=4/√Φ
=(8√5-8)1/2
π²=16/Φ
=(8√5-8)
e=MC²
e=M(8√5-8)
___________
e=8M√5-8M
M=e(√5+1)/32
Now those look awfully familiar... 8M looks like a shadow of 8r passing through √5
whereas M looks to be in the form of Φ. What happens if/when we also set M to Φ?
e=MC²
e=Φ(8√5-8)
e=16
16=Φπ²
1=Φπ²/16
The equality above shown implies that Einstein's
e=MC² is a valid coupling only because 16=Φπ²
rationally precedes it.
Additionally:

the Reimann Hypothesis is certainly true by Ananke. By clarifying the nature of the relationship between the real and imaginary number systems through the function f(x)= x⁴ + 16x² - 256 whose root is 4/√Φ and/or (8√5-8)1/2, an axes is revealed which couples/fixes and subsequently governs the real and imaginary numbers via the immutably integral conduit of real element x=4 and imaginary element x=4i such to solve 256 and -256 respectively.The real part of every non-trivial zero of the Riemann zeta function is 1/2.
As for the "Squaring the Circle":
Wherein (√1+2√4)1/2 yields 51/2, the 2√4 implying the birotation of the photon
as well as the 2x2 axes based on the bidirection/biorientation symmetry of the pentagram.
And as for unity in the context of Reciprocal Systems of Theory:
And as for Miles and when it comes to "Squaring the Circle", one must recognize this endeavor is not strictly speaking a problem of only mathematical nature, as questions need be asked transcending any/all mathematical context(s). The missing of the significance of a square '4' in relation to a rounding π, despite Miles' technical ability having deduced it (the same discipline to ever-receive ongoing accolades) should have been the key focus. The lack of focus on this relation in particular, particularly reflects in/as Miles appropriating a radius and/or circumference to a square. The circumference of a circle is the product of an irrational, whereas the radius is the product of a rational. Therefor, 4/√Φ may concern any/all 1, Φ, √Φ "Kepler" relations as they may (and do) exist in nature, naturally. These oversights are highlighted not out of desire for undermining Miles in any way: to the contrary, I endeavor to see Miles consider his own derived "Charge Field" and be honest with himself in asking and adjudicating, for himself, is he able to both clearly and succinctly define both the words "charge" and "field"? What precisely is a "charge"? And what precisely is a "field"? Such that if/when one permutes "Charge Field" one comprehensively captures the essence of all there is?
I leave those questions with Miles to his person, while reminding him that RS² already has two such clear and succinct postulates which together captures the essence of all there is: motion.
If we live in a universe of motion as postulated, π of 4 is implicit, wherein π ≠ 3.14159...R/S System of Theory Postulates:
1. The universe is composed of one component, motion, existing in three dimensions, in discrete units, and with two reciprocal aspects, space and time.
2. The universe conforms to the relations of ordinary mathematics, its primary magnitudes are absolute, and its geometry is Projective.
...π must be in some relation to/as 4. A ratio is also a relation. For example, s/t is a relation.
Some space about some time. Thus they can not ever be "rationally" severed from one another.
Reciprocal Systems has honored this inseparability from day one by acknowledging space and time
as reciprocal aspects of motion. This implies s/t x t/s = 1 and the reason unity begins (and ends)
from a proper rationing of ones own constituency.
Thanks to the work of the late Dewey B. Larson and late Mr. Bruce Peret et al., Reciprocal Systems of Theory already has (had) the groundwork laid for the unification of space and time from-the-onset by having already found them to be multiplicative reciprocal aspects of motion. This is crucial because it preemptively safeguards space and time from ever being autonomous from one another: they are merely reciprocal aspects of, as Larson's book title implies, Nothing But Motion, and we can measure this motion (in discrete units) from two related reciprocal perspectives: v (velocity) as s/t and/or e (energy) as t/s, the constituency of one being the reciprocal of the other whose multiplicative relation (s/t x t/s = 1) both implicitly and explicitly concerns 1, thus unity.
The extent to which we have accomplished the purpose of our existence depends on the nature of the structure that we have built, not on the amount of sunshine during the progress of the work.
-Dewey B. Larson