************************
ADDENDUM: 04-16-2020
f(x)=x⁴+16x²-256
roots in 4/√Φ thus:
±√9.88854381999...
±i√25.88854381999...
Consider:
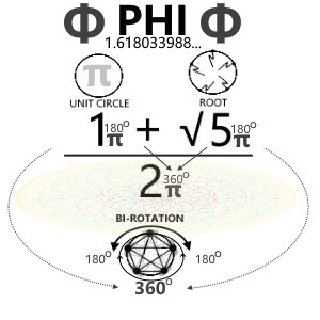
1 = UNITY
√Φ = non-terminating, ≠1
Φ = PROGRESSION (irrational, non-terminating, constituency of '1' concerning UNITY).
Φ² = DISCRETION (Φ+1) (irrational + rational and discrete '1' concerning UNITY∞NOT ).
Φ³ = GRAVITATION (√5+2) (irrational and discrete '2' +concerning DUALITY).
{s³/t ∞ t³/s}
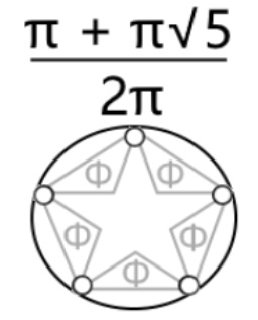
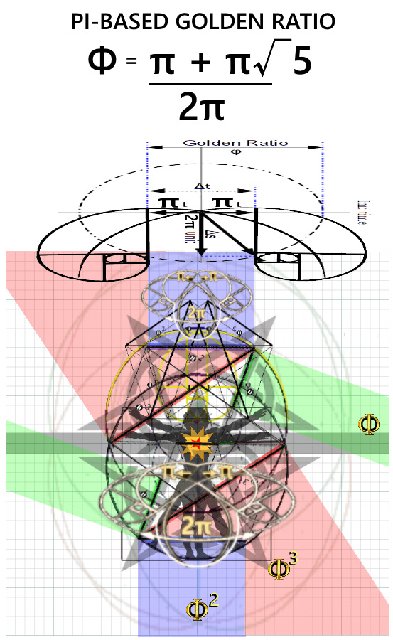
Recalling π=4/√Φ, π²=9.88854381999..., thus
"empower" π=4/√Φ viz.
π²=16/Φ and "rationalize" one side
16 = Φπ² and "compare" to Einstein's General Relativity:
e=MC² and solve for UNITY
1=Φπ²/16
viz. 1 "discrete" unit of absolute magnitude.
Because the four roots of f(x)=x⁴+16x²-256
are as two pairs of conjugates (±r, ±i)
whose both internal (±) and external (1:16)
variables are known, this axes directly relates to
the Reimann Hypothesis which states:
The axes (which conjoins the real and imaginary number systemsReimann Hypothesis:
The real part of every non-trivial zero of the Riemann zeta function is 1/2.
as needed and utilized by the concerned Reimann zeta function
is described by the two pairs (2x2) of conjugate roots of f(x)=x⁴+16x²-256
wherein x=4/√Φ=π, hence x²=π²=9.88854381999... an irrational number,
*however*, recall this number represents 16/Φ=9.88854381999... a ratio.
Thus it can be known that the constituency of the concerned irrational
is actually composed of a ratio of one rational (r) on one irrational (i) or (1r:1i),
which both implicitly and explicitly (ie. of fixed, or "scalar" nature) concerns the integer '16',
as is the case with Φ and 1.618... Imaginary numbers enter the equation by taking the square
of -(1-√5)/2 as i√(2(1-√5))/2, bridging real and imaginary, rational and irrational.
It thus follows that due to the symmetry of the real/imaginary axes according to the roots of f(x)=x⁴+16x²-256,
the Reimann Hypothesis is true by Ananke (necessity).
Later, I will show how this can be used to construct an expression which captures unity,
the progression Φ and gravitation Φ³ as a ± conjugate viz. Φ² ± Φ = 1, Φ³ or
"discretion to/from progression" equals "unity" and "gravity".
************************
************************
Original Post (modified 04-16-2020):
____________________________________________________________________
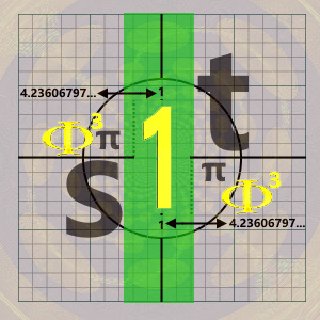
I have recovered a "rational" expression[/u] whose inverse identities are one another: 1 and Φ³.
This relates to the "progression" and gravitation of the physical universe respectively.
This expression (which is also a psuedo-quadratic) relates to the Reimann Hypothesis in that
it proves that all non-trivial zeros have nowhere else to go but the 1/2 line, therefor the algorithm which determines
the distribution of primes is attainable. This identity is the real value of '1' in relation to both: Φ and π
all in a single expression whose multiplicative inverse is Φ³. Therefor, Φ³/1 and 1/Φ³
is where the real number system begins/ends (ie. as like an ∞ fabric) whose "sum" is -1/12.
https://www.youtube.com/watch?v=0Oazb7IWzbA
The reason for this strange sum relates to the numerator/denominator
progressively collapsing from bases 180→90→45→36→18→*16→*12
whose symmetric "pattern" is a consistent 9→9→9→9→9→*7→*3
ending with 12π/144π:
11/12 → 12/12 = 1/12
13/12 → 12/12 = -1/12
11/12 → (+) 1/12 → ***!1!*** ← 1/12 (-) ← 13/12
therefor the actual "sum" of -1/12 is an artifact, but this artifact is pointing to something extremely important:
because the real number system is enclosed, the identity of the psuedo-quadratic "encodes" information about the primes
such that the whole number '1' in relation to Φ and π is the "blueprint" of all possible primes. This would predict that the identity
must always remain '1' regardless of how many √ operations are performed on it.
I am very sorry to hear of Bruce's health issues - I hope his health endures to find this,
I know it will make RS2 stronger, if not a new 'theory of everything' inductively rooted
in the same language the universe itself obeys.