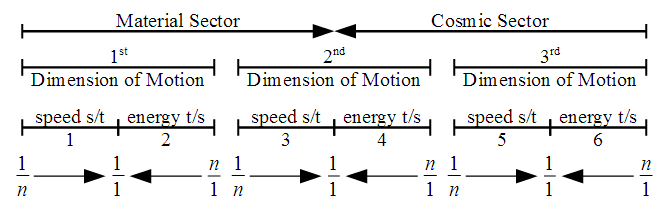
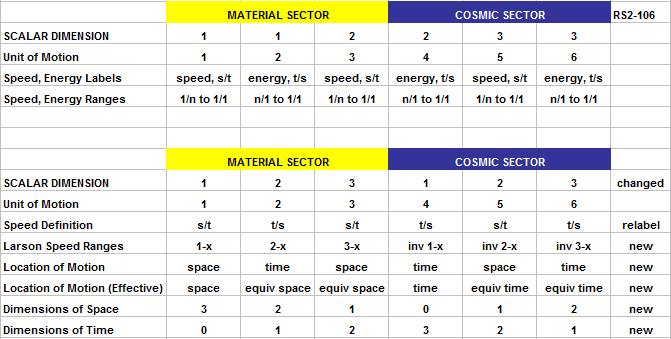
The second diagram (top portion) contains the same information as the preceding, but in my format. The second diagram (bottom portion) presents additional information which needs to be verified. Significantly, it updates the scalar dimension where motion occurs. I don’t know if this is correct, but I know that the scalar dimension associations shown in the original RS2-106 diagram are in doubt due to the work presented in RS2-109.
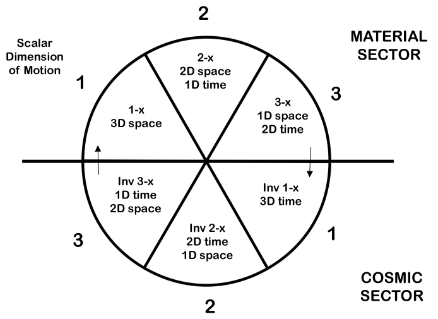
The third diagram uses a circular format to more clearly indicate the flow of motion into an adjacent area. By redefining the scalar dimension where the motion occurs, the three scalar dimensions are all similar in that they link together (within a scalar dimension) the matching Larson speed ranges (i.e. 1-x with inv 1-x). Also, with this definition, the corresponding ranges (e.g. 1-x and inv 1-x) are opposed in the diagram.
Any comments or corrections?