With the passing of Bruce Peret, it is apparent more than ever that we (i.e. members of ISUS) now face the challenge of clarifying where the RST stands, in the context of the organization. Therefore, this topic is intended to clarify the work of the LRC in this historical context, which will require some reference to the RS2 work, for the benefit of those who are only familiar with it.
In order to maintain the necessary continuity of thought, extensive discussion of the fundamentals, as they arise, should take place in the "Discussion on Scalar Motion Fundamentals" topic of this forum. In this present topic, I intend to show how, given the fundamental postulates of Larson's new system of physical theory, the LRC's RSt (hereinafter "RSt" ) was developed with the intent to avoid the most frequent criticism leveled at Larson's work, by attempting to find a way to do it mathematically. Conseuently, prolonged discussions inserted into the thread will be too distracting and prevent the desired continuity of thought, in the presentation of the theoretical development. So, please help me to do that by not posting large, graphic or quote intensive or alternative theory, comments here, but feel free to post them in the associated topic indicated above.
I'll begin the actual presentation in the next post, first with a preface, in order to set the theroretical context, both in terms of RST events and developments and in terms of legacy system of physical theory (LST) events and developments, which prove to be relevant to the RSt development. Second, I will review the lines of thought that led to the development of the new mathematical ideas, as well as the observations of the limits and inadequacies of the LST mathematics, which make it cumbersome, if not inapproriate for the RSt development. Finally, I will show how the two, the new physical and mathematical concepts, have led to unprecedented results that need to be properly understood and hearlded.
The LRC's RSt in Context
Moderator: dbundy
Re: The LRC's RSt in Context
Preface - Part 1
The Reciprocal System based physical theory (RSt) that is being developed at the Dewey B. Larson Memorial Research Center (LRC) begins with the fundamental postulates of Larson's new system of theory, which posit a universe of motion, rather than a universe of matter; That is to say, it is a universe consisting of nothing but motion, which is the title of Volume One of Larson's three volume set of publications, comprising his Structure of the Physical Universe. Volume Two of the set, entitled, Universe of Motion, deals with the astronomical application of Larson's own Reciprocal System based physical theory (his RSt), developed in Volume One. Volume Three of the set is an analysis of most physical properties of matter and radiation, in light of his RSt.
It is an immense work, and has the distinction of being the first general physical theory of the universe ever published. However, many find it inaccessible due to the fact that it is mostly described by Larson in unfamiliar terms and from an unfamiliar point of view. For example, he writes:
When the International Society of Unified Science (ISUS) was formed to support and promote Larson's work, the ambiguity in his texts made for lively discussions about poorly understood areas of the theory, but he was available to clarify what he meant. After he passed away, however, his authority was sorely missed, resulting in a competition of sorts for favorite speculations.With the advent of the Internet, these discussions went online, and took on a whole new dimension.
At the same time, the Internet made many topics in the LST much more accessible to non-professionals, many of whom found the science of quantum mechanics becoming much less daunting, as professionals produced online materials explaining and discussing their esoteric concepts like never before, and historians recounted the various science dramas that were part of the community producing the final form of this mysterious subject. In the context of this heightened interest and familiarity with physical theory, Larson's work was fascinating, since not only his atomic model, but his electrical, magnetic and gravitational concepts were so straight forward and appealing, on the basis of their logical unity. At that point in time, the major problem seemed to be how to get the work seriously considered by the LST community.
Nevertheless, it was becoming more and more clear that spreading the word that Larson had achieved something spectacular was not going all that well. There was a big disconnect between the LST community professionals, steeped in years of studying wave equations and symmetry groups and Lie algebras, and ISUS people trying to make a distinction between vector motion and magnitude only scalar motion and trying to assert that a strong case could be made against the LST's quantum mechanics, its atomic model, its spacetime gravity, its black holes and much, much more.
Consequently, there was much talk in ISUS discussions about "a crucial experiment," one that could prove or predict something that could only be understood through Larson's work, generating enough interest in it for it to be taken seriously by professional members of the LST community. Alas, as the years went by, it became obvious that something was amiss. Many more prominent, long-term members of ISUS, who had rubbed shoulders with Larson in ISUS conferences around the country, faded into oblivion, and those who still participated in online discussions and reading and writing for the ISUS publication Reciprocity, were pointing out difficulties with the work. The concept of the photon was problematic, the atomic spectra couldn't be accounted for and the equation of gravity was incomplete, etc.
Thus, things were ripe for change, when I was elected President of ISUS.
(to be continued)
The Reciprocal System based physical theory (RSt) that is being developed at the Dewey B. Larson Memorial Research Center (LRC) begins with the fundamental postulates of Larson's new system of theory, which posit a universe of motion, rather than a universe of matter; That is to say, it is a universe consisting of nothing but motion, which is the title of Volume One of Larson's three volume set of publications, comprising his Structure of the Physical Universe. Volume Two of the set, entitled, Universe of Motion, deals with the astronomical application of Larson's own Reciprocal System based physical theory (his RSt), developed in Volume One. Volume Three of the set is an analysis of most physical properties of matter and radiation, in light of his RSt.
It is an immense work, and has the distinction of being the first general physical theory of the universe ever published. However, many find it inaccessible due to the fact that it is mostly described by Larson in unfamiliar terms and from an unfamiliar point of view. For example, he writes:
This is a profound statement to be sure, so Larson goes on to explain several aspects of its philosophical nature in eight full paragraphs, not including a paragraph from another author whom he quotes, before he turns "to the question as to what kinds of motion are possible at the basic level." in his theoretical development. This makes for interesting reading for many readers, who don't intend to master the theory, but it's frustrating for those whose interest is piqued enough to attempt to do so. Words are fine and necessary, but they are inevitably ambiguous, without charts, diagrams, and/or equations to illustrate and make their meaning certain for those studying the new material, and Larson provides very little in the way of such helps in his books.Larson, in NBM, Cht 4 wrote:...the question as to what any observed entity or phenomenon is never arises [in this work]. We always know what it is. It is a motion, a combination of motions, or a relation between motions. The only question that is ever at issue is what kinds of motions are involved.
When the International Society of Unified Science (ISUS) was formed to support and promote Larson's work, the ambiguity in his texts made for lively discussions about poorly understood areas of the theory, but he was available to clarify what he meant. After he passed away, however, his authority was sorely missed, resulting in a competition of sorts for favorite speculations.With the advent of the Internet, these discussions went online, and took on a whole new dimension.
At the same time, the Internet made many topics in the LST much more accessible to non-professionals, many of whom found the science of quantum mechanics becoming much less daunting, as professionals produced online materials explaining and discussing their esoteric concepts like never before, and historians recounted the various science dramas that were part of the community producing the final form of this mysterious subject. In the context of this heightened interest and familiarity with physical theory, Larson's work was fascinating, since not only his atomic model, but his electrical, magnetic and gravitational concepts were so straight forward and appealing, on the basis of their logical unity. At that point in time, the major problem seemed to be how to get the work seriously considered by the LST community.
Nevertheless, it was becoming more and more clear that spreading the word that Larson had achieved something spectacular was not going all that well. There was a big disconnect between the LST community professionals, steeped in years of studying wave equations and symmetry groups and Lie algebras, and ISUS people trying to make a distinction between vector motion and magnitude only scalar motion and trying to assert that a strong case could be made against the LST's quantum mechanics, its atomic model, its spacetime gravity, its black holes and much, much more.
Consequently, there was much talk in ISUS discussions about "a crucial experiment," one that could prove or predict something that could only be understood through Larson's work, generating enough interest in it for it to be taken seriously by professional members of the LST community. Alas, as the years went by, it became obvious that something was amiss. Many more prominent, long-term members of ISUS, who had rubbed shoulders with Larson in ISUS conferences around the country, faded into oblivion, and those who still participated in online discussions and reading and writing for the ISUS publication Reciprocity, were pointing out difficulties with the work. The concept of the photon was problematic, the atomic spectra couldn't be accounted for and the equation of gravity was incomplete, etc.
Thus, things were ripe for change, when I was elected President of ISUS.
(to be continued)
Re: The LRC's RSt in Context - Preface Part 2
Preface - Part 2
Struggling to deal with the theroretical problems of Larson's work without him, most of the active ISUS members looked to Professor K.V.K. Nehru, whose credentials and competence in science and prominence in ISUS made him the defacto heir apparent to Mr. Larson, in the eyes of many members. He had written articles in the ISUS journal "Reciprocity" that were controversial, because they seemed to fundamentally alter the work of Larson:
As President of ISUS, I took a keen interest in learning the Reciprocal System and had ideas of my own on how to approach some of the theoretical issues, having won some level of confidence, because I had put together the "Wheel of Motion," which was written up in an article published in Reciprocity. I also began to do serious research on the new system, when I discovered the work of Stephen Wolfram's New Kind of Science.
However, it was apparent to me that these three different directions of research were not going to be able to be accommodated by the organization of ISUS, lest one or the other one won out in a political struggle. Therefore, I proposed forming a research center within ISUS, to be called the Dewey B. Larson Memorial Research Center (LRC), where these different directions of research could be pursued by the researchers and published by ISUS, without insinuating official endorsement of any one in particular, but where, on the other hand, freedom of thought would not be hampered.
Alas, this was not to be, as I insisted that whatever research direction was taken under the auspices of the LRC would have to conform to the new system. I proposed that the acronym for the new system be RST, and that any RST-based theoretical development be designated as an RSt, with the lower-case "t" indicating that it was an RST-based theory, thus distinguishing between the Reciprocal System of Physical Theory and a theory developed under that System. I saw this as vital after reading a Reciprocity article by Mr. Larson entitled, A Rejoinder to K.V.K. Nehru.
When I lost the political battle to impose these conditions (of conforming to the new system that were given by Mr. Larson) on all LRC sponsored research, I resigned from the Presidency and formed my own LRC outside of ISUS. The result was that, over the years, ISUS ended up endorsing and indeed becoming identified with the RS2 effort, which changed the system, just as I had foreseen, introducing ideas that were not only non-conforming to the new system, but even spiritual in nature.
Meanwhile, I formed the LRC and continued with my personal research efforts, which I will proceed to outline next.
Struggling to deal with the theroretical problems of Larson's work without him, most of the active ISUS members looked to Professor K.V.K. Nehru, whose credentials and competence in science and prominence in ISUS made him the defacto heir apparent to Mr. Larson, in the eyes of many members. He had written articles in the ISUS journal "Reciprocity" that were controversial, because they seemed to fundamentally alter the work of Larson:
Thus, a serious schizm began to develop between members of ISUS over theoretical issues of the work. Eventually, this led to the formation of the Re-evaluation of Larson's Reciprocal System, referred to today as the RS2. In the meantime, however, Ronald Satz, one of the most prominent members of the Society was most recalcitrant, and insisted that he was actually the appointed heir to Mr. Larson, having been the actual organizer of ISUS at its inception. Satz had also published a booklet on the Reciprocal System of Larson entitled, The Unmysterious Universe.Nehru wrote:Some students of the Reciprocal System (RS) have been disputing the explanation of the intrinsic
structure of the photons, given by Larson, the originator of the RS. No amount of discussion, so far,
seemed to throw additional light in overcoming the logical objections raised. An examination of the
situation undertaken by the present investigator revealed that a crucial fact of fundamental nature is
being missed hitherto, both by the originator and the other students. It is found that a recognition of this
fact not only clarifies the photon situation entirely but also throws light on many collateral issues where
gaps in the logical development of the theory exist, thus rendering the theory more cogent. Some of
these new developments are reported in this paper. (See here.)
As President of ISUS, I took a keen interest in learning the Reciprocal System and had ideas of my own on how to approach some of the theoretical issues, having won some level of confidence, because I had put together the "Wheel of Motion," which was written up in an article published in Reciprocity. I also began to do serious research on the new system, when I discovered the work of Stephen Wolfram's New Kind of Science.
However, it was apparent to me that these three different directions of research were not going to be able to be accommodated by the organization of ISUS, lest one or the other one won out in a political struggle. Therefore, I proposed forming a research center within ISUS, to be called the Dewey B. Larson Memorial Research Center (LRC), where these different directions of research could be pursued by the researchers and published by ISUS, without insinuating official endorsement of any one in particular, but where, on the other hand, freedom of thought would not be hampered.
Alas, this was not to be, as I insisted that whatever research direction was taken under the auspices of the LRC would have to conform to the new system. I proposed that the acronym for the new system be RST, and that any RST-based theoretical development be designated as an RSt, with the lower-case "t" indicating that it was an RST-based theory, thus distinguishing between the Reciprocal System of Physical Theory and a theory developed under that System. I saw this as vital after reading a Reciprocity article by Mr. Larson entitled, A Rejoinder to K.V.K. Nehru.
When I lost the political battle to impose these conditions (of conforming to the new system that were given by Mr. Larson) on all LRC sponsored research, I resigned from the Presidency and formed my own LRC outside of ISUS. The result was that, over the years, ISUS ended up endorsing and indeed becoming identified with the RS2 effort, which changed the system, just as I had foreseen, introducing ideas that were not only non-conforming to the new system, but even spiritual in nature.
Meanwhile, I formed the LRC and continued with my personal research efforts, which I will proceed to outline next.
Re: The LRC's RSt in Context
Determined to develop a physical theory under the new system, or an RST-based RSt, which could be understood in terms of a closed form equation, I had a lot to learn. However, I don't intend to retrace all the steps and deadends that I churned my way through, during the process, but rather to explain it from the point of view that I can see now, but couldn't see then.
In retrospect, we can see that a lot of what Larson developed under the new system was necessarily without any knowledge of the LST community's data, which he was not privy to, as an outside investigator. His college friend and roommate, Linus Pauling, went on to learn quantum mechanics and become a prominent part of the LST community at Caltech, Stanford and other universities, winning much notoriety and two Nobel prizes in the process, while Larson had to self-publish his works and is even denied a mention in Wikipedia!
Pauling joined the faculty of Caltech, during the high point of the quantum physics drama in 1927. Einstein had explained the photoelectric effect in terms of Planck’s quantum units (E = hf), Bohr had explained the atom in terms of nucleus orbiting electrons, interacting with quantum units (photons) (λ = h/mv)) and Pauli had calculated the Zeeman spectra in terms of four quantum numbers, including the spin of electrons, while Heisenberg/Schrödinger/Dirac were inventing the new quantum mechanics, with Pauli’s four quantum numbers. It was a heady time to be a physicist/chemist in the LST community.
One can only imagine what it must have been like for Larson, having little or no first-hand access to the wrestlings of LST researchers, who were trying to make sense of quantum phenomena, in terms of non-commutative mathematics (i.e. matrix multiplication), seeing energy come in discrete units of angular momenta divided by 4π, yet measuring electron spin to be + or – 1/2 times h/2π (ħ) (i.e. spin 1/2) and photon spin as -1, 0, +1 times ħ (i.e. spin 1), but plagued by not knowing how to incorporate spin 1/2 into a relativistic wave equation, until Dirac’s mathematical "acrobatics" pulled it off in his relativistic equations that actually predicted quantum spin, in order to conserve the angular motmentum of the electron. I doubt that Larson understood in those days why they would later say,
Yet, unfortunately, not recognizing this state of affairs, ISUS was unable to preserve Larson's insight that instinctively knew that nature didn't need to be described with non-commutative mathematics and non-Euclidean geometry. Instead, they've changed the system, his fundamental postulates, dropping those assumptions to accommodate the RS2. But then, what did Larson know of quantum spin and Pauli matrices and wave equations? Nothing, probably, yet what did he know of numbers and geometry in general? Could he have possibly known of the Greek Tetraktys, binomial expansion, Pascal's Triangle and their amazing connections with Euclidean geometry and his stack of 2x2x2 = 8 unit cubes, that I would later name in his honor? He may have known more than we know he knew. Wouldn't that have been simply amazing, if it were true?
I wish he were here now, so that he could see how amazing it really is, and how he could have shocked the world, had he known, and had he taken a different turn in his thinking. I'll elaborate on that next time.
(to be continued)
In retrospect, we can see that a lot of what Larson developed under the new system was necessarily without any knowledge of the LST community's data, which he was not privy to, as an outside investigator. His college friend and roommate, Linus Pauling, went on to learn quantum mechanics and become a prominent part of the LST community at Caltech, Stanford and other universities, winning much notoriety and two Nobel prizes in the process, while Larson had to self-publish his works and is even denied a mention in Wikipedia!
Pauling joined the faculty of Caltech, during the high point of the quantum physics drama in 1927. Einstein had explained the photoelectric effect in terms of Planck’s quantum units (E = hf), Bohr had explained the atom in terms of nucleus orbiting electrons, interacting with quantum units (photons) (λ = h/mv)) and Pauli had calculated the Zeeman spectra in terms of four quantum numbers, including the spin of electrons, while Heisenberg/Schrödinger/Dirac were inventing the new quantum mechanics, with Pauli’s four quantum numbers. It was a heady time to be a physicist/chemist in the LST community.
One can only imagine what it must have been like for Larson, having little or no first-hand access to the wrestlings of LST researchers, who were trying to make sense of quantum phenomena, in terms of non-commutative mathematics (i.e. matrix multiplication), seeing energy come in discrete units of angular momenta divided by 4π, yet measuring electron spin to be + or – 1/2 times h/2π (ħ) (i.e. spin 1/2) and photon spin as -1, 0, +1 times ħ (i.e. spin 1), but plagued by not knowing how to incorporate spin 1/2 into a relativistic wave equation, until Dirac’s mathematical "acrobatics" pulled it off in his relativistic equations that actually predicted quantum spin, in order to conserve the angular motmentum of the electron. I doubt that Larson understood in those days why they would later say,
Of course, what we clearly understand now, so many decades later, is that they still don't comprehend why quantum mechanics works, if and only if, they use that machinery of Dirac's, which depends on non-commutative mathematics and the magic of imaginary numbers. In contrast to Larson, who had the advantage of a fundamental insight that they lacked, they couldn't break with the past, where everything was defined in the one-dimensional physics of simple harmonic motion, i.e. vectorial motion. The mathematical machinery that they found so useful in adapting old ideas to new phenomena might have been unknown to Larson the outsider, but his vision of a whole new paradigm of physics was completely unknown to them and still is.Paul Sutter wrote:It’s only through Dirac's mathematical machinery that we can make predictions about spin behaviors that we need in order to do physics. Thus we have an unfortunate case where the only way to answer the question ‘What is spin?’ is to simply point at the math of Dirac and shrug. (see here)
Yet, unfortunately, not recognizing this state of affairs, ISUS was unable to preserve Larson's insight that instinctively knew that nature didn't need to be described with non-commutative mathematics and non-Euclidean geometry. Instead, they've changed the system, his fundamental postulates, dropping those assumptions to accommodate the RS2. But then, what did Larson know of quantum spin and Pauli matrices and wave equations? Nothing, probably, yet what did he know of numbers and geometry in general? Could he have possibly known of the Greek Tetraktys, binomial expansion, Pascal's Triangle and their amazing connections with Euclidean geometry and his stack of 2x2x2 = 8 unit cubes, that I would later name in his honor? He may have known more than we know he knew. Wouldn't that have been simply amazing, if it were true?
I wish he were here now, so that he could see how amazing it really is, and how he could have shocked the world, had he known, and had he taken a different turn in his thinking. I'll elaborate on that next time.
(to be continued)
Re: The LRC's RSt in Context - 3D vs 1D Oscillation
Is assuming a universe of nothing but motion a radical departure from the Newtonian system of physical theory? Is it ever, but who could have known back in the hey day of quantum mechanics and quantum field theory that the particle zoo of the experimentalists would finally be organized by what would become the symmetry groups of the standard model of particle physics, SU(3)xSU(2)xU(1) and heralded throughout the world and down through the decades of the 20th Century and into the 21st Century with no end in sight? Asserting that the universe is not made of these particles, indeed, that these particles are not elementary at all, simply falls on deaf ears, even as physicists around the world argue for building even bigger mega-machines to crash them into one another, trying to understand why "two is not equal to three," as they say.
Well, Larson didn't need to build a $22 billion dollar machine to find the answer. He only needed to understand that rotational motion cannot be scalar motion. Had he realized that, he might have concluded that the 1d "direction" reversals he introduces in Nothing But Motion, needed to be three-dimensional. Had he done that, he probably would have discovered the mysterious world of quantum spin and the answer to the question "why two is not equal to three," which Arkani-Hamed is dying to know. So much so, he wants the world to build him a $22 billion machine to find out. Wow, and we can't even get Larson a page on Wikipedia!
But let's not get ahead of our story. First we have to understand the naturalness of numbers and geometry. That naturalness is found in the integers, which are derived from rational numbers. I wish I could tell the whole story, because it's definitely fascinating, but suffice it to say that physicists should not depend on mathematicians to give them what they need. You see, Pauli studied spin and spin states and, using the mathematics of mathematicians, he found that the number of required spin states for different particles is equal to their spin times two plus one. So, since the observed spin of fermions, such as quarks and leptons, is 1/2 hbar, they must have two spin states: 2 x 1/2 = 1 and 1 plus 1 is 2 states: +1/2 and -1/2.
Now bosons, such as photons, have spin 1, so 2 x 1 = 2 and 2 plus 1 is 3 states: -1, 0, +1. Moreover, composite particles, such as nucleons, have spin 3/2, so 2 x 3/2 = 3 and 3 plus 1 is 4 states: -3/2, -1/2, +1/2, +3/2. This is great, but why? No one in the LST community really knows what spin is, so they can't really tell us why this formula of Wolfgang Pauli, 2s+1, works but it does.
Yet, Larson would have known what spin is, and he would have known why 2s+1 gives the number of possible spin states for these entities, had he made his "direction" reversals 3d instead of 1d. Just why that is so, is the subject we discuss in the next post.
(to be continued)
Well, Larson didn't need to build a $22 billion dollar machine to find the answer. He only needed to understand that rotational motion cannot be scalar motion. Had he realized that, he might have concluded that the 1d "direction" reversals he introduces in Nothing But Motion, needed to be three-dimensional. Had he done that, he probably would have discovered the mysterious world of quantum spin and the answer to the question "why two is not equal to three," which Arkani-Hamed is dying to know. So much so, he wants the world to build him a $22 billion machine to find out. Wow, and we can't even get Larson a page on Wikipedia!
But let's not get ahead of our story. First we have to understand the naturalness of numbers and geometry. That naturalness is found in the integers, which are derived from rational numbers. I wish I could tell the whole story, because it's definitely fascinating, but suffice it to say that physicists should not depend on mathematicians to give them what they need. You see, Pauli studied spin and spin states and, using the mathematics of mathematicians, he found that the number of required spin states for different particles is equal to their spin times two plus one. So, since the observed spin of fermions, such as quarks and leptons, is 1/2 hbar, they must have two spin states: 2 x 1/2 = 1 and 1 plus 1 is 2 states: +1/2 and -1/2.
Now bosons, such as photons, have spin 1, so 2 x 1 = 2 and 2 plus 1 is 3 states: -1, 0, +1. Moreover, composite particles, such as nucleons, have spin 3/2, so 2 x 3/2 = 3 and 3 plus 1 is 4 states: -3/2, -1/2, +1/2, +3/2. This is great, but why? No one in the LST community really knows what spin is, so they can't really tell us why this formula of Wolfgang Pauli, 2s+1, works but it does.
Yet, Larson would have known what spin is, and he would have known why 2s+1 gives the number of possible spin states for these entities, had he made his "direction" reversals 3d instead of 1d. Just why that is so, is the subject we discuss in the next post.
(to be continued)
Re: The LRC's RSt in Context
What happened, when Hamilton invented the quaternions, is hard to overestimate. He didn't like imaginary numbers, because they weren't intuitive, but he didn't know there was any other choice, and maybe there wasn't, when dealing with calculating locations on a sphere. His algebraic couples worked well for locations on the complex plane. They were a straightforward, logical way to think of two-dimensional numbers, so why didn't algebraic triples work for three dimensions?
We normally just glaze over this question, reciting the amusing story of Hamilton's children inquiring each morning, if he had found a way to multiply them. Yet sadly, he could only add them, not multiply them, until that fateful walk along the river, when the idea he needed became clear to him. He knew it was a momentous moment and took the time to carve the formula into the stone of the bridge, but retelling that story over and over again, seems to evade the real story, which only begins with the question: "Why did it require four numbers, instead of three to make his calculations?"
Not that it makes that much difference to most people. As one commentator puts it:
We need to pause and ask ourselves why? The ancient Greeks did a lot of thinking about it that we might regard as quaint and naive today. Although the only numbers they had were integers and ratios of integers, they knowing nothing of negative and imaginary numbers, of course, may have understood something that modern man has neglected. For them the number one (our 1/1) was the father of numbers, the monad of unity (think of our unit progression and the LST's Higgs field.) The number two, the dyad, represented the power of duality (think of our less than c-speed, space oscillation, and greater than c-speed, time oscillation), which was reconciled in the harmony of the number three, the triad, (think of our two identical S|T and T|S combos, seen as one, splitting our two opposed combos, (2S|T and S|2T), which unites the monad and the dyad, and which is then completed in the number four, the tetrad, (think of our set of four S|Ts combos and our set of four T|S combos ) forming the perfect unity of a higher order, the ten numbers of the dekad - the tetraktys:
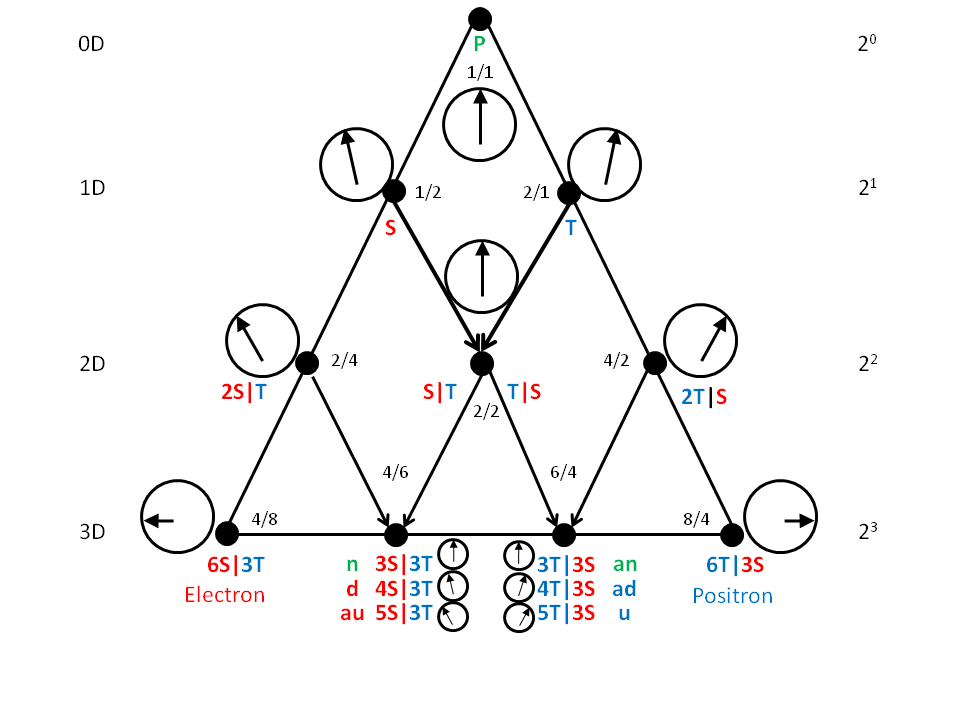
Figure 1. When the scalar motion and combinations of scalar motion, as developed in the LRC's RSt, are mapped to the tetraktys, the standard model entities of LST particle physics naturally appear, due to its four dimensions and their associated "directions" (n=neutrino, d=down quark, au=antiup quark, and an=antineutrino, ad=antidown quark, u=up quark.)
In figure 1 above, we see that the development of the LRC's RSt, unwittingly followed the dimensions and "directions" of the tetraktys, something that we will soon see is of fundamental importance, although unreachable, using the dimensions and directions of LST mathematics and particle physics.
The lesson here is that before modern researchers dismiss this ancient thought of the Greeks, it would be good to remember that the biggest puzzle and obstacle to understanding the physical world today still remains the inability of the LST to reconcile the discrete with the continuous. Geometry consists of both right lines and circles, but numbers only come as discrete quantities (at least they did at the time of the Greeks, before the acceptance of the modern invention of "real" numbers.) Greek numbers are hopelessly discrete, no matter how real. The war with Nebecker is not over yet, though, and the truth is, it never will be, until the proper connection between the properties of discrete numbers and the properties of continuous geometry is recognized.
Actually, we now know that the properties of numbers are magnitude, dimension and "direction," while the properties of geometry are magnitude, dimension and direction. They go together, like hand and glove. The use of real numbers, matrices and vectors have served us well, and no one can deny that, but in the end they simply don't work for scalar motion, where motion is not defined by the changing location of an object in a coordinate system, or a changing value on a complex plane, or a changing point somewhere on a sphere. We need to understand something much more sublime. We need to understand that the tetraktys holds the key to uniting discrete numbers with continuous magnitudes.
(to be continued)
We normally just glaze over this question, reciting the amusing story of Hamilton's children inquiring each morning, if he had found a way to multiply them. Yet sadly, he could only add them, not multiply them, until that fateful walk along the river, when the idea he needed became clear to him. He knew it was a momentous moment and took the time to carve the formula into the stone of the bridge, but retelling that story over and over again, seems to evade the real story, which only begins with the question: "Why did it require four numbers, instead of three to make his calculations?"
Not that it makes that much difference to most people. As one commentator puts it:
However, when it is recognized that the reason that the four numbers of the quaternions are twice the two numbers of the complexes, and that the two numbers of the complexes are twice the one number of the reals, and that the eight numbers of the octonions are twice the four numbers of the quaternions, is due to the fact that there are two "directions" in each each dimension of nature, we should definitely pause and rethink what has happened.[T]he fact remains that the man in the street is strangely averse to using quaternions. Side by side with matrices and vectors, now the lingua franca of all physical scientists, quaternions appear to exude an air of nineteenth-century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions, but such enthusiasm means little to the harder-headed physical scientist.
We need to pause and ask ourselves why? The ancient Greeks did a lot of thinking about it that we might regard as quaint and naive today. Although the only numbers they had were integers and ratios of integers, they knowing nothing of negative and imaginary numbers, of course, may have understood something that modern man has neglected. For them the number one (our 1/1) was the father of numbers, the monad of unity (think of our unit progression and the LST's Higgs field.) The number two, the dyad, represented the power of duality (think of our less than c-speed, space oscillation, and greater than c-speed, time oscillation), which was reconciled in the harmony of the number three, the triad, (think of our two identical S|T and T|S combos, seen as one, splitting our two opposed combos, (2S|T and S|2T), which unites the monad and the dyad, and which is then completed in the number four, the tetrad, (think of our set of four S|Ts combos and our set of four T|S combos ) forming the perfect unity of a higher order, the ten numbers of the dekad - the tetraktys:

Figure 1. When the scalar motion and combinations of scalar motion, as developed in the LRC's RSt, are mapped to the tetraktys, the standard model entities of LST particle physics naturally appear, due to its four dimensions and their associated "directions" (n=neutrino, d=down quark, au=antiup quark, and an=antineutrino, ad=antidown quark, u=up quark.)
In figure 1 above, we see that the development of the LRC's RSt, unwittingly followed the dimensions and "directions" of the tetraktys, something that we will soon see is of fundamental importance, although unreachable, using the dimensions and directions of LST mathematics and particle physics.
The lesson here is that before modern researchers dismiss this ancient thought of the Greeks, it would be good to remember that the biggest puzzle and obstacle to understanding the physical world today still remains the inability of the LST to reconcile the discrete with the continuous. Geometry consists of both right lines and circles, but numbers only come as discrete quantities (at least they did at the time of the Greeks, before the acceptance of the modern invention of "real" numbers.) Greek numbers are hopelessly discrete, no matter how real. The war with Nebecker is not over yet, though, and the truth is, it never will be, until the proper connection between the properties of discrete numbers and the properties of continuous geometry is recognized.
Actually, we now know that the properties of numbers are magnitude, dimension and "direction," while the properties of geometry are magnitude, dimension and direction. They go together, like hand and glove. The use of real numbers, matrices and vectors have served us well, and no one can deny that, but in the end they simply don't work for scalar motion, where motion is not defined by the changing location of an object in a coordinate system, or a changing value on a complex plane, or a changing point somewhere on a sphere. We need to understand something much more sublime. We need to understand that the tetraktys holds the key to uniting discrete numbers with continuous magnitudes.
(to be continued)
Re: The LRC's RSt in Context
In the post above, we see that the magnitudes, dimensions and "directions" (polarities), of numbers, reflected in the tetraktys, allow us to map discrete units of scalar motion, as developed logically in the LRC's RSt, and identify these scalar motion combinations with the first generation of the LST's standard model of fermions and bosons, with all the anti-particles and their proper electrical charges included. This is an amazing achievement of the system that should be recognized for what it is. However, that is not all.
There are three generations of fermions and bosons and the LST cannot explain why. Nevertheless, the legacy community does know one amazing fact about these three generation of particles: Their masses are amazingly inter-related. This remarkable relationship was discovered by Yoshio Koide and is known as the Koide Formula.
Neither the LST community, nor the LRC are able to unravel the mystery of the relative masses of the three generations of particles, just yet. However, there have been some promising developments lately at the LRC, which will be explained later. First, though, it's important to understand how the other two generations are formed in our RSt.
Recall that we have shown that the magnitudes, dimensions and "directions" of the numbers in the tetraktys are equivalent to the geometry of the magnitudes, dimensions and directions of Larson's 2x2x2 stack of unit cubes (LC). Now, since we see that the first generation particles of the standard model map to the tetraktys, in terms of scalar motion combinations, it should also map to the LC, since they are equivalent.
The good news is that since the points, lines, areas and cubes of the LC correspond to the magnitudes, dimensions and "directions" of the tetraktys, there is a built-in correspondence between the standard model particles and the LC. However, because there is a significant conceptual difference between scalar "directions" and vectorial directions, the polarities of what we might call the scalar tetraktys have to be treated differently than the vectorial directions of the reference system (i.e. left - right, up - down, forward and backward, directions) In the vector case, for instance, we can swap a 1d segment on the right side of the center point, for the segment of the line on the left side of the center point and it makes no difference to the figure we draw.
To the contrary, however, replacing a scalar space oscillation, which is on the low side of c-speed, with a scalar time oscillation, which is on the high side of c-speed, makes a huge difference, because the two are inverses of one another. Indeed, such a swapping constitutes what is called the "anti" characteristic of the standard model particles. Therefore, the polarity - opposite polarity nature of the scalar motion combos is conserved in all dimensions of the scalar tetraktys, whereas it is not in the vector tetraktys. This is shown in the graphic of the previous post by the "directional" indicators, added for each combo of the tetraktys.
This difference also accounts for the fact that the scalar tetraktys follows the numbers of the Pascal triangle, where the 3d dimension sequence is 1 3 3 1, but apparently not the accompanying binary expansion sequence, which is 1 2 4 8. The 1331 sequence counts the dimensional subunits of the LC (1 0d point, 3 1d combos, 3 2d combos & 1 3d combo), while the 1 2 4 8 sequence counts its "directional" subunits (1 "direction" (point), 2 "directions" (line), 4 "directions" (plane) and 8 "directions" (cube), which are not readily apparent in the scalar tetraktys. This is why it's possible to have the electron - positron pair occupying the two limits of the scalar sequence: 1 3 3 1 in our scalar map, but leaves us wondering why the electron could have 1 "direction," while the positron has 8 "directions," counted as 1 (is there a stack of 8 unit "cubes" in the positron?)
Nevertheless, if we consider the degrees of freedom at each dimension in the four "spaces" of the third dimension (fourth counting 0) of the scalar tetraktys, we can see that the 1 2 4 8 sequence of directions in the vectorial tetraktys is also present in the scalar tetraktys, as 1, 2, 4 and 8 possible degrees of freedom, in the respective dimensions, as shown in the graphic below:
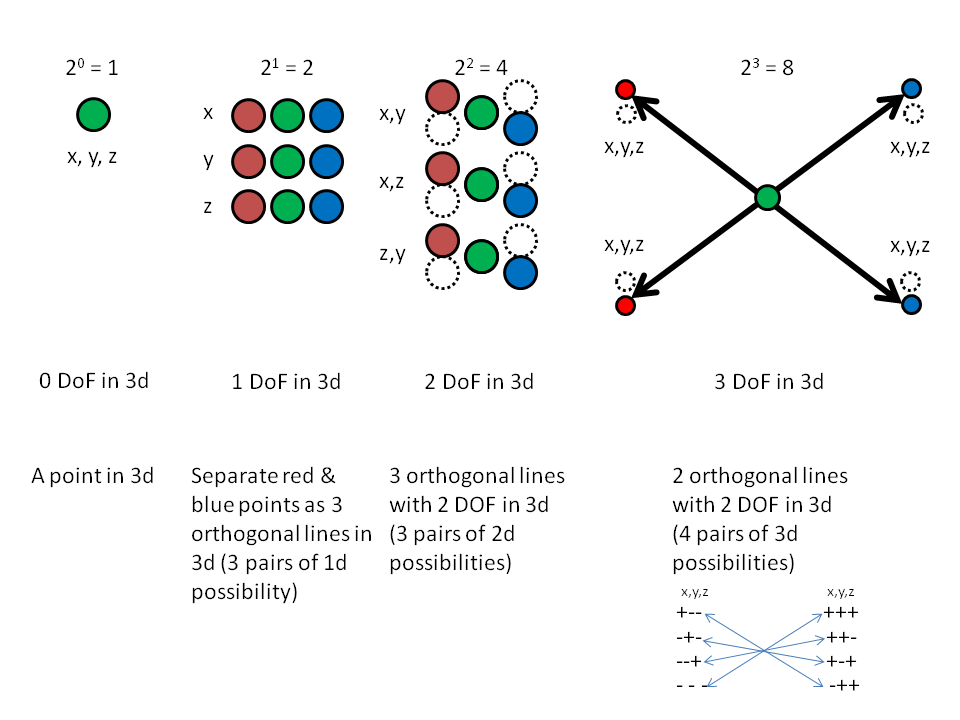
So, it turns out that these two views (the Pascal triangle (dimensional count- 1331) & the LC ("directional" count- 1248) are both legitimate maps of scalar combos to the tetraktys, just as they are in the familiar vector map. Now, why is this important? The reason is that the LC gives us the relationship between the discrete magnitudes of numbers in the tetraktys and the continuous magnitudes of geometry in the LC, the elusive understanding that has evaded the LST community for so long. Furthermore, it provides the means for generating the three families of observed particles, as we shall see next time.
(to be continued)
There are three generations of fermions and bosons and the LST cannot explain why. Nevertheless, the legacy community does know one amazing fact about these three generation of particles: Their masses are amazingly inter-related. This remarkable relationship was discovered by Yoshio Koide and is known as the Koide Formula.
Neither the LST community, nor the LRC are able to unravel the mystery of the relative masses of the three generations of particles, just yet. However, there have been some promising developments lately at the LRC, which will be explained later. First, though, it's important to understand how the other two generations are formed in our RSt.
Recall that we have shown that the magnitudes, dimensions and "directions" of the numbers in the tetraktys are equivalent to the geometry of the magnitudes, dimensions and directions of Larson's 2x2x2 stack of unit cubes (LC). Now, since we see that the first generation particles of the standard model map to the tetraktys, in terms of scalar motion combinations, it should also map to the LC, since they are equivalent.
The good news is that since the points, lines, areas and cubes of the LC correspond to the magnitudes, dimensions and "directions" of the tetraktys, there is a built-in correspondence between the standard model particles and the LC. However, because there is a significant conceptual difference between scalar "directions" and vectorial directions, the polarities of what we might call the scalar tetraktys have to be treated differently than the vectorial directions of the reference system (i.e. left - right, up - down, forward and backward, directions) In the vector case, for instance, we can swap a 1d segment on the right side of the center point, for the segment of the line on the left side of the center point and it makes no difference to the figure we draw.
To the contrary, however, replacing a scalar space oscillation, which is on the low side of c-speed, with a scalar time oscillation, which is on the high side of c-speed, makes a huge difference, because the two are inverses of one another. Indeed, such a swapping constitutes what is called the "anti" characteristic of the standard model particles. Therefore, the polarity - opposite polarity nature of the scalar motion combos is conserved in all dimensions of the scalar tetraktys, whereas it is not in the vector tetraktys. This is shown in the graphic of the previous post by the "directional" indicators, added for each combo of the tetraktys.
This difference also accounts for the fact that the scalar tetraktys follows the numbers of the Pascal triangle, where the 3d dimension sequence is 1 3 3 1, but apparently not the accompanying binary expansion sequence, which is 1 2 4 8. The 1331 sequence counts the dimensional subunits of the LC (1 0d point, 3 1d combos, 3 2d combos & 1 3d combo), while the 1 2 4 8 sequence counts its "directional" subunits (1 "direction" (point), 2 "directions" (line), 4 "directions" (plane) and 8 "directions" (cube), which are not readily apparent in the scalar tetraktys. This is why it's possible to have the electron - positron pair occupying the two limits of the scalar sequence: 1 3 3 1 in our scalar map, but leaves us wondering why the electron could have 1 "direction," while the positron has 8 "directions," counted as 1 (is there a stack of 8 unit "cubes" in the positron?)
Nevertheless, if we consider the degrees of freedom at each dimension in the four "spaces" of the third dimension (fourth counting 0) of the scalar tetraktys, we can see that the 1 2 4 8 sequence of directions in the vectorial tetraktys is also present in the scalar tetraktys, as 1, 2, 4 and 8 possible degrees of freedom, in the respective dimensions, as shown in the graphic below:

So, it turns out that these two views (the Pascal triangle (dimensional count- 1331) & the LC ("directional" count- 1248) are both legitimate maps of scalar combos to the tetraktys, just as they are in the familiar vector map. Now, why is this important? The reason is that the LC gives us the relationship between the discrete magnitudes of numbers in the tetraktys and the continuous magnitudes of geometry in the LC, the elusive understanding that has evaded the LST community for so long. Furthermore, it provides the means for generating the three families of observed particles, as we shall see next time.
(to be continued)