A few weeks ago, I had the privilege of presenting our new scalar model of the atom to a group at ISUS headquarters, in SLC, UT. It is a presentation of three parts, but I only presented parts 1 & 2. Part 3 is yet to be presented at some future date. Because not everyone is familiar with the LRC's RSt, part 1 explains the basics of the theory. Part 2 discusses how the new scalar-motion atomic model generates the general structure of the spectral groups and how that allows us to format the periodic table as four concentric circles, capturing the reciprocity of the eight sub-periods and the ascending order of the four periods.
I didn't present part 3, because it's supposed to show the actual calculations of the spectra of a given element. The group was surprised to learn that the LST's wave equation can only be used to calculate the Hydrogen and Helium spectra, since it cannot be solved for three or more electrons. However, the LST community says it works "in principle" for the others (see here.)
Of course, our new scalar-motion model is not based on the principles of vector motion associated with orbiting electrons. In fact, if we go all the way back to the fundamental basis of the LST's quantum mechanics, the de Broglie equation, where the idea of wave/particle duality started ( λ = h/mv), we have to take issue with the whole concept, because our model is only a combo of oscillating space (time) and time (space), but more on that later.
The most immediate challenge is to account for the line spectra of the elements in our new model. Though the complete answer is not yet available, the beginning point is the scalar motion equation, where the middle term equals the inner portion of the space and time oscillations:
S|T = 1/2 + 1/1 + 2/1 = 4|4
This is the LRC's scalar motion equation of the photon, combinations of which, as we've shown, lead to our standard model of particles and, most recently, the periodic table of elements. In the process, we've discovered the reciprocal nature of the eight sub-periods of the table, making up its four periods. Now we want to be able to take a given element of the table and calculate its line spectra, something the LST community can't do with their quantum mechanics and its wave equation.
Nevertheless, the accomplishments of their vector-motion based model are quite impressive. They use the four so-called quantum numbers in their wave equation to model the empirical data, even though they can't solve that wave equation for many body calculations. However, the concepts of mass, energy, angular momentum and quantum spin, together with Planck's constant have enabled them to move forward, in spite of the mysterious quantum mysteries that emerge from the little understood concept of quantum spin and the de Broglie equation.
Coming up with a whole new model that can replace this LST model of spinning, orbiting electrons, the binding energy of which counteracts and balances the energy of the angular momentum produced by the moving masses, even though that energy gets shielded by the electrons in the closest orbits to the nucleus, until the outward energy of the momentum overcomes the energy of the inward electrical attraction, ionizing the atom, is a tremendous challenge.
Fortunately, we too have an outward versus inward force, which models the same behavior, where, as the outward force increases, with each new photon absorbed, the inward force is eventually overcome and the atom is ionized. To understand this model, we need to examine the middle term of our scalar motion equation. Recall that the equation for the positively charged proton is:
S|T = 10/20 + 10/13 + 26/13 = 46|46 num, and for the negatively charged electron, it is:
S|T = 6/12 + 6/3 + 6/3 = 18|18 num.
The value for the middle s/t term of the proton, the inward portion, which is the motion corresponding to the LST concept of electrical charge, is 13-10 = 3, while for the electron, it is 3-6 = -3, so they normally balance out each other for a total of 16/16, or unity. This would be equivalent to what is termed the "ground state of Hydrogen," in the LST model. Since the displacement from unity of the inner term is greater to the time side (> 1/1) of the unit progression in the proton, we label its "charge" as "positive," and since it is greater to the space side (< 1/1) in the electron, we label its "charge" as "negative."
Now, if we add a photon to the electron, it adds a 1/1 balanced unit to the total s/t of its inner term:
S|T = (6/12 + 6/3 + 6/3) + (1/2 + 1/1 + 2/1) = 7/14 + 7/4 + 8/4 = 22|22
So the space displacement of the electron (4-7 = -3) remains unchanged, but the "strength" or energy of the atom, as a combination of the proton and electron, has increased to 17/17, from 16/16. It's important to note that this 1-unit increment in the inner term of the atom is due to the addition of the photon's 4|4 num, which reminds us of the unexplained number 4 in Balmer's equation, and the constant in Rydberg's equation, obtained when Balmer's constant is divided by 4 and inverted from wavelength (λ) to wave number (1/λ).
What happened (as we've explained previously) is that Balmer discovered that, if he multiplied his constant times the ratio of n/(n - 4), where n = (m2) and m => 3, he could calculate the observed wavelengths of the line spectra of Hydrogen. However, this limited the range of the calculations to the third quantum level and above, because 12 - 4 = -3 and 22 - 4 = 0. Rydberg solved this problem later, simply by rearranging the terms. He divided Balmer's constant by 4 and inverted his equation for wavelength to an equation of wave number, obtaining:
1/λ = R(1/n12 - 1/n22), n1 > n2
which enabled the calculation to start from the ground state and increase from there.
On this basis, Neils Bohr proposed his atomic model, which worked well for Hydrogen's single electron, but failed for the other elements, with multiple electrons. We were able to also calculate Hydrogen's line spectra, based on the scalar motion equation, but we were not prepared to follow the LST into the world of the wave equation solution, since it is based on the dimensional character of the 3d coordinate system and it was difficult to see how a combination of space and time oscillations had the necessary dimensional characteristics.
However, now that we have overcome that challenge, we are faced with finding the equivalent of the LST community's outward centrifugal force of angular momentum versus the inward centripetal force of electrical charge concept, in the context of 1d, 2d and 3d orbitals, which constitutes their accepted vector motion model.
In the next post, I will outline our approach to that challenge.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
My last entry was April 20th, four months ago. I wish I could say that I've been busily engaged in furthering the research of this thread, but the truth is I haven't even thought about it. It's been a four month hiatus for me, and I'm afraid I've lost the momentum that we had built up after the discovery of the reciprocity of the periodic table.
I'm not sure of the implications this new discovery brings to the table, and I feel much more inclined to ponder those possibilities than slog through the complexities of trying to find a way to calculate the atomic spectra of the elements, as the next step. The prospect of the latter is not nearly as appealing to me, as that of the former.
Given that, and the fact that the unfamiliar demands of the new single life as a widower, with which I'm now trying to cope, have proven to be a significant personal distraction, I think I will close out this thread and open a new one. I don't know what it will be yet, but, hopefully, it'll come to me soon.
I'm not sure of the implications this new discovery brings to the table, and I feel much more inclined to ponder those possibilities than slog through the complexities of trying to find a way to calculate the atomic spectra of the elements, as the next step. The prospect of the latter is not nearly as appealing to me, as that of the former.
Given that, and the fact that the unfamiliar demands of the new single life as a widower, with which I'm now trying to cope, have proven to be a significant personal distraction, I think I will close out this thread and open a new one. I don't know what it will be yet, but, hopefully, it'll come to me soon.
Re: Meeting a Terrific Challenge
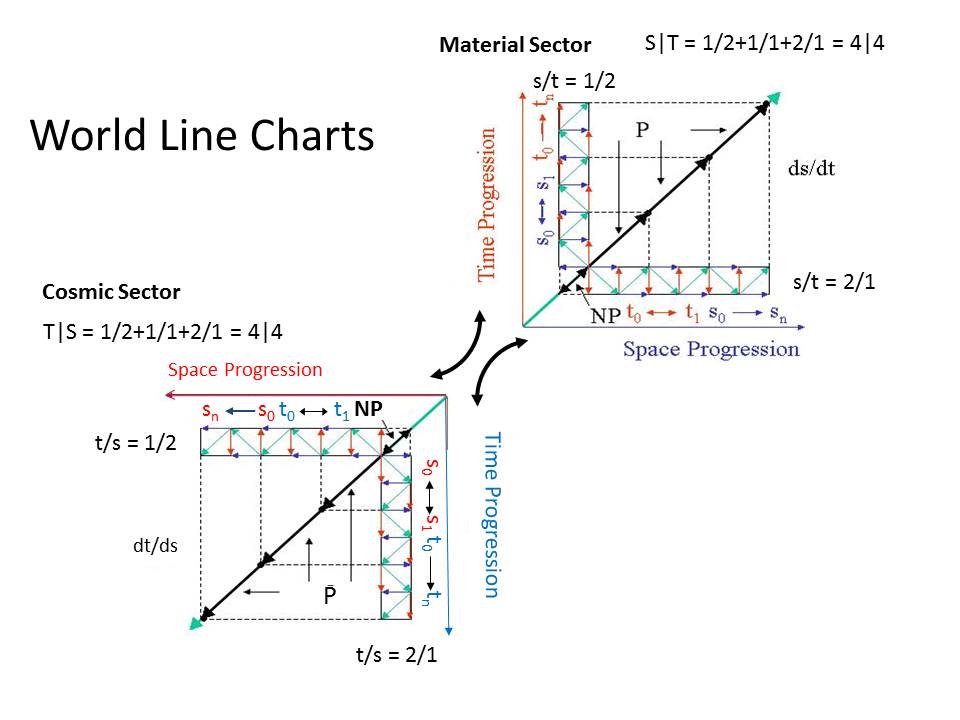
For starters, green diagonal arrows zig-zaging horizontally are not the same as green horizontal arrows. Please be precise in your geometric expressions.dbundy wrote: ↑Sun Oct 28, 2018 4:22 pm
- Gray dashed lines: The two units of space and time comprising one unit (cycle) of motion (s/t = (1+1)/2 and 2/(1+1)).
Black diagonal arrows: Unit space/time progression; that is, one unit of space increase for one unit of time increase (s/t = 1/1). Although, the length of the black arrows is two units long.
Red vertical arrows: Unit time progression.
Blue horizontal arrows: Unit space progression.
<...snip...>dbundy wrote: ↑Thu Feb 07, 2019 2:27 pm
The green, zig-zaging, arrows are increasing vertically upwards, and the green, zig-zagging, arrows are increasing horizontally to the right in the MS, and vertically downwards and horizontally to the left in the CS.
These are representations of space and time oscillations.
IMO these diagonal-green arrows are redundant on your diagram because the directions of the small horizontal blue arrows and the small vertical red arrows, already represent space and time oscillations.
Notice that on the MS diagram you marked two independent axes, namely the horizontal blue axis tiled "Space progression" and the vertical red axis titled "Time Progression". You also marked the directions of these axes with little arrows at their ends.
I interpret this, that all small horizontal blue arrows directions are expressed relatively to the direction of the horizontal blue axis ...and conversely, all small vertical red arrows directions are expressed relatively to the direction of the vertical red axis.
Please confirm or deny the latter interpretation of directions in the MS diagram.
Re: Meeting a Terrific Challenge
Hi Horace,
You wrote:
You wrote:
You wrote:
Yes, that's correct, however, I added the green arrows to show the resultant of the red and blue arrows together.For starters, green diagonal arrows zig-zaging horizontally are not the same as green horizontal arrows. Please be precise in your geometric expressions.
IMO these diagonal-green arrows are redundant on your diagram because the directions of the small horizontal blue arrows and the small vertical red arrows, already represent space and time oscillations.
You wrote:
That is correct. The small blue arrows (space) reverse "direction," as time progresses uniformly (small red arrows), along the vertical axis, while the small red arrows (time) reverse "direction," as space progresses uniformly (small blue arrows), along the horizontal axis.Notice that on the MS diagram you marked two independent axes, namely the horizontal blue axis tiled "Space progression" and the vertical red axis titled "Time Progression". You also marked the directions of these axes with little arrows at their ends.
I interpret this, that all small horizontal blue arrows directions are expressed relatively to the direction of the horizontal blue axis ...and conversely, all small vertical red arrows directions are expressed relatively to the direction of the vertical red axis.
Please confirm or deny the latter interpretation of directions in the MS diagram.
Re: Meeting a Terrific Challenge
What if BOTH time and space progress non-uniformly ?dbundy wrote: ↑Wed Oct 30, 2019 8:57 am That is correct. The small blue arrows (space) reverse "direction," as time progresses uniformly (small red arrows), along the vertical axis, while the small red arrows (time) reverse "direction," as space progresses uniformly (small blue arrows), along the horizontal axis.
For simplicity, let's limit our discussion to 2 units of motion (i.e.: ΔS1|ΔT1 and ΔS2|ΔT2 ).
Re: Meeting a Terrific Challenge
Over the years, I've considered the possibility of a simultaneous oscillation of both the space and time aspects of an S unit or a T unit, but I have never been able to get anywhere with the idea. Only in the combination of the two into an S|T unit, where one or the other aspect of the S or T motion is oscillating, can I make any progress.
Re: Meeting a Terrific Challenge
That is because your mind is stuck in a rut. I would like to get you out of it very much, because your other work about the number of directions in multidimensional motion, the tetraktys, etc... are fine. My motives are altruistic.
Once your mind is freed out of this rut, who knows what greatness it can accomplish.
That is because an alternative is not possible ...the key out of the rut is understanding why.
The answer in a nutshell is: "homotopic equivalence"...but that requires further explanation.
For starters: In order to have an oscillation of any kind, you need at least two units of motion. Do you agree ?
For example, one unit of motion: +ΔS1 | +ΔT1 and a second unit of motion: -ΔS2 | +ΔT2.
...where the two consecutive signs ' + ' and ' - ' indicate the reversal.
For the sake of simplicity, let us assume that these ± signs collectively denote the directions in ALL available dimensions, because at this stage I want to avoid the discussion about the 1D vs. 3D oscillation ( which is an important issue in general, but not for the sake of this discussion )
Re: Meeting a Terrific Challenge
Hoarce wrote:
However, lets discuss it in a separate topic. I have some important things to say about E = mc2 in this one. I'll start it and call it Discussions on Scalar Motion Fundamentals," if that's ok.
Yes, I agree absolutely.For starters: In order to have an oscillation of any kind, you need at least two units of motion. Do you agree ?
For example, one unit of motion: +ΔS1 | +ΔT1 and a second unit of motion: -ΔS2 | +ΔT2.
...where the two consecutive signs ' + ' and ' - ' indicate the reversal.
However, lets discuss it in a separate topic. I have some important things to say about E = mc2 in this one. I'll start it and call it Discussions on Scalar Motion Fundamentals," if that's ok.
Re: Meeting a Terrific Challenge
OK, lets continue in this thread.
Re: Meeting a Terrific Challenge
Doug have you seen Wolfram's latest?
https://writings.stephenwolfram.com/202 ... beautiful/
Could his computational "graph" be useful for the Reciprocal System? https://www.wolframphysics.org/
Some recent youtube videos:
Stephen Wolfram: Cellular Automata, Computation, and Physics | AI Podcast #89 with Lex Fridman
https://www.youtube.com/watch?v=ez773teNFYA
History of Physics
https://www.youtube.com/watch?v=acUf7PuGWXA
Wolfram Physics Project Launch
https://www.youtube.com/watch?v=rbfFt2uNEyQ
Wolfram Physics Project: Working Session Friday, Apr. 17, 2020
https://www.youtube.com/watch?v=8bdA_g1F06M
Mike
https://writings.stephenwolfram.com/202 ... beautiful/
Could his computational "graph" be useful for the Reciprocal System? https://www.wolframphysics.org/
Some recent youtube videos:
Stephen Wolfram: Cellular Automata, Computation, and Physics | AI Podcast #89 with Lex Fridman
https://www.youtube.com/watch?v=ez773teNFYA
History of Physics
https://www.youtube.com/watch?v=acUf7PuGWXA
Wolfram Physics Project Launch
https://www.youtube.com/watch?v=rbfFt2uNEyQ
Wolfram Physics Project: Working Session Friday, Apr. 17, 2020
https://www.youtube.com/watch?v=8bdA_g1F06M
Mike