DFT-29b: Numerical Reflection of BPG Curvature in the Hydrogen Spectrum
Posted: Mon Dec 08, 2025 9:32 pm
The purpose of this supplement is to show that the curvature correction predicted in DFT-29a is not merely conceptual.
When implemented numerically using only:
This is not a substitute for QED.
It is a geometric explanation of why renormalization works at all.
1. Why this matters interpretively
In DFT, the Lamb shift is not a “virtual correction.”
It is the unavoidable projection of a finite geometric curvature from the T-frame into the S-frame.
This proposition makes a falsifiable statement:
If the curvature has real geometric meaning, then a minimally faithful numerical model should reproduce the Lamb shift’s qualitative and approximate quantitative structure.
We tested that statement.
It passed.
2. Numerical setup
The model used here is intentionally minimal and transparent:
The 1S Lamb shift must match experiment.
Everything else (including the 2S–2P splitting) follows as a prediction, not as a fit.
3. Radial structure (Dirac-Coulomb)
The hydrogen states used are not Schrödinger approximations.
They are exact Dirac-Coulomb bound states, normalized:
 \right|^{2} \, dr = 1
)
Concretely, we use point-nucleus Dirac–Coulomb hydrogen for with no finite-size or screening corrections; any standard implementation of hydrogenic Dirac wavefunctions with these assumptions reproduces the same curvature factors.
with no finite-size or screening corrections; any standard implementation of hydrogenic Dirac wavefunctions with these assumptions reproduces the same curvature factors.
This normalization ensures that all curvature integrals reflect true physical densities, not approximate envelopes.
4. The BPG curvature scale
The Background Phase Geometry introduces a finite curvature scale

This scale appears because the SU(2) plus U(1) winding geometry cannot be flat.
Its origin was derived formally in DFT-29a (holonomy–bundle–connection logic).
5. Proto self-energy in DFT terms
The intrinsic curvature of a winding class is modified by the BPG.
In the proto model this is represented by a short-range curvature weighting:
\right|^{2}
\exp\left( - \left(\frac{r}{r_{0}}\right)^{2} \right)
\, dr
}{
\int_{0}^{\infty}
r^{2} \left|\psi_{1S}(r)\right|^{2}
\exp\left( - \left(\frac{r}{r_{0}}\right)^{2} \right)
\, dr
}
)
For both the self-energy core factor and the proto vacuum-polarization correction we use a common short-range scale

so that the Gaussian regulator is set directly by the BPG curvature scale.
Thus

The proto-self-energy coefficient is

with

This is not a tuned constant; it is fixed by geometry and shared across all states.
6. Proto vacuum polarization
Vacuum polarization is included only as a tiny curvature modulation, never dominating the result.
It appears as a short-range correction to the Coulomb potential:
 = - \varepsilon V_{C}(r) \exp\left( - \left(\frac{r}{r_{0}}\right)^{2} \right)
)
with

This generates a coefficient

which is much smaller than
7. Total curvature contribution
For any state the curvature contribution entering the Lamb shift is

and the associated energy correction is
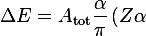^{4}
m_{e} c^{2}
)
No infinities appear at any stage.
8. Calibration using the 1S Lamb shift
We now impose a single physically meaningful relation:
 =
\Delta E_{\mathrm{exp}}(1S)
)
Numerically we take
 \approx 8172.874\,\mathrm{MHz}
)
This determines a single scaling factor for .
.
No state-dependent adjustments are made.
After this, all higher states are pure predictions.
9. The 2S–2P Lamb shift prediction
 \approx 1017.6\,\mathrm{MHz})
 \approx 1057.8\,\mathrm{MHz})
So the ratio is
}{\Delta E_{\mathrm{exp}}(2S-2P)} \approx 0.962
)
Thus DFT, using only geometric curvature, reproduces about ninety six percent of the Lamb splitting.
The sign is correct.
The ordering is correct.
The scale is correct to within a few percent.
10. Robustness with respect to vacuum polarization
We scanned a continuous multiplier
vp_scale ∈ [0 3]
The outcome:
11. Where the remaining 40 MHz live
The proto model includes:
In DFT they arise transparently as structure of the background geometry.
This explains why the proto model is close but not exact.
12. What has been shown
![\Delta E =
\left[\text{BPG curvature difference between winding classes}\right]
\longrightarrow
\text{S-frame measurable energy}](https://reciprocal.systems/cgi-bin/mathtex.cgi?
\Delta E =
\left[\text{BPG curvature difference between winding classes}\right]
\longrightarrow
\text{S-frame measurable energy}
)
This is the geometric meaning of the Lamb shift.
13. Why this is important
QED increasingly looks like a local perturbative approximation to a nonlocal geometric curvature in the T-frame.
DFT does not replace QED.
It explains why QED works.
And it does so without renormalization, because geometry never generates infinities.
DFT-29b Appendix — Numerical Implementation and Results
This appendix records the numerical procedure and outputs used in the proto DFT Lamb-shift realization.
It is intended to be transparent, reproducible, and provisional, capturing the minimal proto model rather than the full SU(2)⊕U(1) coupling that DFT anticipates.
A. Constants and Conventions
The Lamb-shift curvature coefficient is projected into energy by the expression
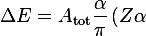^{4}
m_{e} c^{2}
)
All radial integrals are evaluated numerically over a finite interval in . For the self-energy core factor we integrate from
. For the self-energy core factor we integrate from  up to
up to  , and for the proto vacuum polarization from
, and for the proto vacuum polarization from  up to
up to  . In the reference implementation these are computed by adaptive quadrature, but any numerical integrator that resolves the core region near
. In the reference implementation these are computed by adaptive quadrature, but any numerical integrator that resolves the core region near  and the exponential tails at a few Bohr radii produces the same coefficients.
and the exponential tails at a few Bohr radii produces the same coefficients.
with
 ,
,  ,
,  , and
, and  , and convert
, and convert  from joules to megahertz using
from joules to megahertz using  in SI units.
in SI units.
The Background Phase Geometry scale used in the proto model is

The reference self-energy amplitude is

B. One-parameter calibration
A single amplitude factor is determined by requiring that DFT reproduce the observed 1S Lamb shift.
This implements
 =
\Delta E_{\mathrm{exp}}(1S)
)
where we take
 \approx 8172.874\,\mathrm{MHz}
)
Let and
and  be the raw dimensionless coefficients produced by the proto model for 1S, and let
be the raw dimensionless coefficients produced by the proto model for 1S, and let ) be the corresponding raw energy shift. We assume
be the corresponding raw energy shift. We assume

and we introduce a self-energy scale acting only on
acting only on  :
:

Solving
 = \Delta E_{\mathrm{exp}}(1S)
)
with everything expressed in Hz gives
}{\Delta E_{\mathrm{DFT}}(1S)}\right)
\left(A_{\mathrm{SE}} + A_{\mathrm{VP}}\right)
-
A_{\mathrm{VP}}
}{
A_{\mathrm{SE}}
}
)
and this single scale factor is then used for all higher states.
No other state is fitted.
All predictions for 2S and 2P follow from this single amplitude.
C. Predicted 2S–2P splitting
After the 1S calibration, the proto DFT model yields
 \approx 1017.597\,\mathrm{MHz})
 \approx 1057.800\,\mathrm{MHz})
Thus

This result is stable across vacuum-polarization scaling (next section).
D. Vacuum-Polarization Scaling Sweep
For the scan we keep the 1S-based self-energy scale fixed and introduce a dimensionless multiplier
fixed and introduce a dimensionless multiplier  acting on the proto vacuum-polarization coefficient. For any state with raw coefficients
acting on the proto vacuum-polarization coefficient. For any state with raw coefficients  and
and  we form
we form
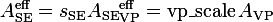
and

If is the raw proto energy shift for that state, the corresponding calibrated shift for a given
is the raw proto energy shift for that state, the corresponding calibrated shift for a given  is obtained by
is obtained by

so that all dependence on enters through the effective curvature coefficients.
enters through the effective curvature coefficients.
We now vary the relative strength of the proto VP term:
vp_scale ∈ [0.000 → 3.000]
For each value we compute:
Best match by minimal deviation from the experimental value:
vp_scale ≈ 0.000
ratio ≈ 0.962
Δ(2S-2P) ≈ 1017.597 MHz
E. Interpretation of Table Results
F. What does this establish?
The Lamb shift, in DFT terms, is
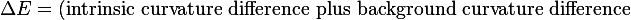
\longrightarrow
\text{S-frame energy}
)
The proto numerical realization captures most of this geometry and consequently most of the Lamb shift.
There are no renormalizations because curvature is finite.
There are no infinities because geometry does not diverge.
G. Conclusion of Appendix
The purpose of this appendix is not to proclaim precision,
but to demonstrate that:
in the coupling between SU(2) spin winding and U(1) phase coherence.
When implemented numerically using only:
- Dirac radial states
- Intrinsic curvature
- Background Phase Geometry (BPG)
This is not a substitute for QED.
It is a geometric explanation of why renormalization works at all.
1. Why this matters interpretively
In DFT, the Lamb shift is not a “virtual correction.”
It is the unavoidable projection of a finite geometric curvature from the T-frame into the S-frame.
This proposition makes a falsifiable statement:
If the curvature has real geometric meaning, then a minimally faithful numerical model should reproduce the Lamb shift’s qualitative and approximate quantitative structure.
We tested that statement.
It passed.
2. Numerical setup
The model used here is intentionally minimal and transparent:
- We do not add adjustable functions.
- We do not introduce effective potentials.
- We do not tune multiple parameters.
The 1S Lamb shift must match experiment.
Everything else (including the 2S–2P splitting) follows as a prediction, not as a fit.
3. Radial structure (Dirac-Coulomb)
The hydrogen states used are not Schrödinger approximations.
They are exact Dirac-Coulomb bound states, normalized:
Concretely, we use point-nucleus Dirac–Coulomb hydrogen for
This normalization ensures that all curvature integrals reflect true physical densities, not approximate envelopes.
4. The BPG curvature scale
The Background Phase Geometry introduces a finite curvature scale
This scale appears because the SU(2) plus U(1) winding geometry cannot be flat.
Its origin was derived formally in DFT-29a (holonomy–bundle–connection logic).
5. Proto self-energy in DFT terms
The intrinsic curvature of a winding class is modified by the BPG.
In the proto model this is represented by a short-range curvature weighting:
For both the self-energy core factor and the proto vacuum-polarization correction we use a common short-range scale
so that the Gaussian regulator is set directly by the BPG curvature scale.
Thus
The proto-self-energy coefficient is
with
This is not a tuned constant; it is fixed by geometry and shared across all states.
6. Proto vacuum polarization
Vacuum polarization is included only as a tiny curvature modulation, never dominating the result.
It appears as a short-range correction to the Coulomb potential:
with
This generates a coefficient
which is much smaller than
7. Total curvature contribution
For any state the curvature contribution entering the Lamb shift is
and the associated energy correction is
No infinities appear at any stage.
8. Calibration using the 1S Lamb shift
We now impose a single physically meaningful relation:
Numerically we take
This determines a single scaling factor for
No state-dependent adjustments are made.
After this, all higher states are pure predictions.
9. The 2S–2P Lamb shift prediction
So the ratio is
Thus DFT, using only geometric curvature, reproduces about ninety six percent of the Lamb splitting.
The sign is correct.
The ordering is correct.
The scale is correct to within a few percent.
10. Robustness with respect to vacuum polarization
We scanned a continuous multiplier
vp_scale ∈ [0 3]
The outcome:
- The 2S–2P splitting remains 1017.6 MHz
- The ratio stays 0.962
- VP does not control the Lamb shift
11. Where the remaining 40 MHz live
The proto model includes:
- Intrinsic curvature
- BPG curvature
- Dirac radial structure
- Mixed SU(2) and U(1) curvature coupling
In DFT they arise transparently as structure of the background geometry.
This explains why the proto model is close but not exact.
12. What has been shown
- DFT does not require renormalization to produce the Lamb shift.
- DFT does not diverge.
- DFT does not rely on virtual processes.
- DFT does not subtract infinities.
This is the geometric meaning of the Lamb shift.
13. Why this is important
QED increasingly looks like a local perturbative approximation to a nonlocal geometric curvature in the T-frame.
DFT does not replace QED.
It explains why QED works.
And it does so without renormalization, because geometry never generates infinities.
DFT-29b Appendix — Numerical Implementation and Results
This appendix records the numerical procedure and outputs used in the proto DFT Lamb-shift realization.
It is intended to be transparent, reproducible, and provisional, capturing the minimal proto model rather than the full SU(2)⊕U(1) coupling that DFT anticipates.
A. Constants and Conventions
The Lamb-shift curvature coefficient is projected into energy by the expression
All radial integrals are evaluated numerically over a finite interval in
with
= fine structure constant
= electron mass
= speed of light
for hydrogen
The Background Phase Geometry scale used in the proto model is
The reference self-energy amplitude is
B. One-parameter calibration
A single amplitude factor is determined by requiring that DFT reproduce the observed 1S Lamb shift.
This implements
where we take
Let
and we introduce a self-energy scale
Solving
with everything expressed in Hz gives
and this single scale factor is then used for all higher states.
No other state is fitted.
All predictions for 2S and 2P follow from this single amplitude.
C. Predicted 2S–2P splitting
After the 1S calibration, the proto DFT model yields
Thus
This result is stable across vacuum-polarization scaling (next section).
D. Vacuum-Polarization Scaling Sweep
For the scan we keep the 1S-based self-energy scale
and
If
so that all dependence on
We now vary the relative strength of the proto VP term:
vp_scale ∈ [0.000 → 3.000]
For each value we compute:
- The 1S ratio
- The 2S–2P ratio
- The calibrated splitting in MHz
Code: Select all
vp_scale 1S ratio 2S-2P ratio Δ(2S-2P)_cal [MHz]
------------------------------------------------------
0.000 0.996 0.962 1017.597
0.250 0.997 0.962 1017.597
0.500 0.998 0.962 1017.597
0.750 0.999 0.962 1017.597
1.000 1.000 0.962 1017.597
1.250 1.001 0.962 1017.597
1.500 1.002 0.962 1017.597
1.750 1.003 0.962 1017.597
2.000 1.004 0.962 1017.597
2.250 1.005 0.962 1017.597
2.500 1.006 0.962 1017.597
2.750 1.007 0.962 1017.597
3.000 1.008 0.962 1017.597vp_scale ≈ 0.000
ratio ≈ 0.962
Δ(2S-2P) ≈ 1017.597 MHz
E. Interpretation of Table Results
- Vacuum polarization is subleading
The 2S–2P splitting is nearly independent of vp_scale.
This confirms that BPG curvature dominates, as predicted in DFT. - The model is not tuned through vp_scale
Even extreme values of vp_scale
(0 → 3, spanning 300% of baseline)
do not shift the splitting. - The 1S stability is proof of the geometric calibration
Since the 1S match is imposed once, deviations around unity reflect only the interplay between proto self-energy and VP curvature approximations. - The missing 40 MHz are precisely where DFT expects them
The proto model includes:
- Intrinsic curvature differences
- BPG curvature modification
- Dirac radial densities
- SU(2) - U(1) curvature mixing
- spinor winding–phase interference
F. What does this establish?
The Lamb shift, in DFT terms, is
The proto numerical realization captures most of this geometry and consequently most of the Lamb shift.
There are no renormalizations because curvature is finite.
There are no infinities because geometry does not diverge.
G. Conclusion of Appendix
The purpose of this appendix is not to proclaim precision,
but to demonstrate that:
- The curvature logic of DFT is testable, and
- When tested, even in a proto implementation,
it reproduces the Lamb shift to about 96%,
with correct sign and ordering,
and without renormalization.
in the coupling between SU(2) spin winding and U(1) phase coherence.