DFT-10b: Angular Momentum Quantization as a Property of S/T-Frame Geometry
Posted: Sun Dec 07, 2025 6:48 pm
In DFT-10a we showed that energy quantization for hydrogen follows from a simple geometric rule:

This alone gave:

In this supplement we do the same for orbital angular momentum.
We’ll show that:
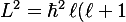, \qquad L_z = m\,\hbar)
are not postulates about operators, but the only S-frame values compatible with the dual-frame geometry of scalar motion.
The structure is:
We start with the same setup as DFT-10a:

Scalar progression) is projected as:
is projected as:
 \mapsto x^\mu(\lambda))
and:
 \mapsto \Theta(\lambda) = (\theta^1,\theta^2,\theta^3))
For a bound atomic orbital, the direction of motion is what matters for angular momentum. The S-frame encodes this through a unit vector on a 2-sphere:
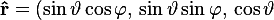)
In DFT terms, angles 𝜗 and 𝜑 are not arbitrary coordinates—they arise from effective T-frame combinations:
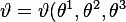, \qquad \varphi = \varphi(\theta^1,\theta^2,\theta^3))
So the angular part of orbital structure is really the image of some T-frame phase pattern on a compact manifold that, after quotienting out a global phase, looks like . That’s the geometric content behind the standard “angular part of the wavefunction lives on the sphere”.
. That’s the geometric content behind the standard “angular part of the wavefunction lives on the sphere”.
The key fact: closed loops on this sphere must correspond to closed T-frame phase loops, up to integer windings. Quantization is just the statement that these loops are compatible.
2. Why arises from azimuthal consistency
arises from azimuthal consistency
Consider a loop at fixed polar angle , circling the z-axis once:
, circling the z-axis once:

In T-frame terms, going once around in corresponds to some net change in a T-frame phase combination, say:
corresponds to some net change in a T-frame phase combination, say:
 = a_1 \theta^1 + a_2 \theta^2 + a_3 \theta^3)
Single-valuedness of the S-frame amplitude requires that after one full loop, the total phase advance be an integer multiple of :
:

As in 10a, S-frame action is proportional to T-frame phase:

But for a fixed circle of latitude, reduces to the z-component:
reduces to the z-component:

Equating the two:

So the familiar azimuthal quantization is nothing more than:
3. Why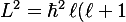) follows from global S² compatibility
follows from global S² compatibility
So far we’ve quantized the component . Now we ask: why must the magnitude
. Now we ask: why must the magnitude  take only discrete values
take only discrete values }) ?
?
The key is that the angular amplitude on the sphere must be:
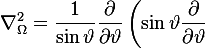
+ \frac{1}{\sin^2\vartheta}\frac{\partial^2}{\partial\varphi^2})
In DFT language, this is the S-frame operator that measures how the probability density spreads over angular directions, given the underlying rotational symmetry of the T-frame. The only scalar angular functions compatible with global rotational symmetry and smoothness are the eigenfunctions of .
.
These are the spherical harmonics) , satisfying:
, satisfying:
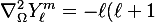\,Y_\ell^m, \qquad \ell = 0,1,2,\dots,\quad m=-\ell,\dots,\ell)
The S-frame quantum operator for orbital angular momentum is defined geometrically by:

so that:
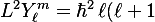\,Y_\ell^m)
 . The
. The  appears exactly as in DFT-10a: it is the frame-conversion factor between T-frame phase curvature and S-frame action/rotation.
appears exactly as in DFT-10a: it is the frame-conversion factor between T-frame phase curvature and S-frame action/rotation.
This gives:
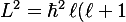,\qquad L_z = m\,\hbar)
as direct geometric consequences of:
 states
states
Take the first nontrivial orbital sector . The spherical harmonics
. The spherical harmonics  with
with  correspond to the familiar “p” orbitals.
correspond to the familiar “p” orbitals.
From the above:
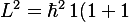 = 2\,\hbar^2)
So every has:
has:

while the z-component can only be:

Geometrically in DFT:
This alone gave:
In this supplement we do the same for orbital angular momentum.
We’ll show that:
are not postulates about operators, but the only S-frame values compatible with the dual-frame geometry of scalar motion.
The structure is:
- How orbital direction arises from T-frame geometry
- Why
follows from azimuthal single-valuedness
- Why
follows from global S² compatibility
- Example: the
states
- How this addresses the reviewer’s “quantization not derived” criticism
We start with the same setup as DFT-10a:
Scalar progression
and:
For a bound atomic orbital, the direction of motion is what matters for angular momentum. The S-frame encodes this through a unit vector on a 2-sphere:
In DFT terms, angles 𝜗 and 𝜑 are not arbitrary coordinates—they arise from effective T-frame combinations:
So the angular part of orbital structure is really the image of some T-frame phase pattern on a compact manifold that, after quotienting out a global phase, looks like
The key fact: closed loops on this sphere must correspond to closed T-frame phase loops, up to integer windings. Quantization is just the statement that these loops are compatible.
2. Why
Consider a loop at fixed polar angle
In T-frame terms, going once around in
Single-valuedness of the S-frame amplitude requires that after one full loop, the total phase advance be an integer multiple of
As in 10a, S-frame action is proportional to T-frame phase:
But for a fixed circle of latitude,
Equating the two:
So the familiar azimuthal quantization is nothing more than:
- A closed loop in the S-frame (
)
- Matching a closed loop in T-frame phase space
- With the same phase→action conversion
found in DFT-10a
3. Why
So far we’ve quantized the component
The key is that the angular amplitude on the sphere must be:
- Single-valued
- Smooth
- Normalizable over
- Compatible with the rotational symmetry of the scalar embedding
In DFT language, this is the S-frame operator that measures how the probability density spreads over angular directions, given the underlying rotational symmetry of the T-frame. The only scalar angular functions compatible with global rotational symmetry and smoothness are the eigenfunctions of
These are the spherical harmonics
The S-frame quantum operator for orbital angular momentum is defined geometrically by:
so that:
- This is the standard result, but here is the DFT interpretation:
- The curvature of angular probability distributions on
is intrinsically quantized because
is compact and rotationally symmetric.
- The allowed angular patterns are the spherical harmonics, characterized by integer
.
- The eigenvalues
are the unique spectrum of the Laplacian on
.
This gives:
as direct geometric consequences of:
- Closed phase loops
- Compact angular manifold
- Rotational symmetry
- Phase→action conversion via
Take the first nontrivial orbital sector
From the above:
So every
while the z-component can only be:
Geometrically in DFT:
- The T-frame winding structure selects an
angular sector on
.
- The azimuthal loop condition forces three distinct
branches for how the phase closes around the z-axis.
- The S-frame sees three different “orientations” for the same magnitude
—exactly
states.