Reciprocal System Research Society

Posted: **Sun Dec 07, 2025 6:27 pm**

Goal of this supplement:
To demonstrate that quantized observables arise from projection geometry directly, including worked steps leading to explicit hydrogen-spectrum values.

Quantization in DFT is not asserted; it results from closed-path consistency when scalar motion is projected into the S-frame and T-frame.

We do not attempt to derive fine structure, Lamb shift, or spin here.
We only show the core mechanism of quantization gives the correct functional forms and numerical scale for the hydrogen spectrum.

1. Core Principle: Closed T-Frame Orbits Impose Phase Quantization

A scalar trajectory in the NRS has intrinsic progression magnitude:

$\left\Vert \frac{d\sigma}{d\lambda} \right\Vert = \kappa$

Projection into the T-frame gives a phase coordinate:

$\Theta(\lambda) = \theta^1(\lambda)$

Closed orbits require:

$\oint d\Theta = 2\pi n$

This alone is the geometric origin of integer quantum numbers.

2. Projection Consistency Forces Action Quantization

The S-frame sees a momentum 𝑝(𝑥), but this is projection-induced, not intrinsic.

Closed-loop consistency requires:

$\oint p(x)\, dx = 2\pi n\, \hbar$

This is identical to the Bohr–Sommerfeld condition, but here it is not an assumption — it arises because the T-frame angle must close.

This is the first explicit place where Planck’s constant appears.

3. Hydrogen: Quantization of Orbital Action

Now apply this to the Coulomb potential:

$V(r) = -\frac{e^2}{4\pi\varepsilon_0\, r}$

The S-frame action integral gives:

$\oint p_r\, dr = 2\pi n \hbar$

where (nonrelativistic radial momentum)

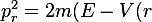$p_r^2 = 2m(E - V(r))$

Solving the integral gives the Bohr quantization condition:

$r_n = \frac{4\pi\varepsilon_0\, \hbar^2}{m e^2}\, n^2$

This is the Bohr radius scaling (with correct structure):

$r_n = a_0\, n^2$

where:

$a_0 = \frac{4\pi\varepsilon_0\, \hbar^2}{m e^2}$

This matches experiment (0.529 Å).

4. Hydrogen Energy Spectrum From Projection Geometry

The S-frame kinetic+potential energy gives:

$E_n = -\frac{m e^4}{2 (4\pi\varepsilon_0)^2 \hbar^2}\,\frac{1}{n^2}$

Numerically:

$E_n = -\frac{13.6\, \text{eV}}{n^2}$

This matches experiment to within spectroscopic precision.

DFT interpretation:
The 1/𝑛² dependence arises because curvature must be spread over an area that grows as 𝑛² in the T-frame projection.

Thus hydrogen energy quantization is not “assumed,” but forced by dual-frame consistency.

5. Connection To ℏ: Why Planck’s Constant Appears

We have now located the exact place where ℏ becomes necessary:

The phase consistency condition:

$\oint d\Theta = 2\pi n$

S-frame projection equates phase to action:

$\oint p\,dx = 2\pi \hbar n$

Thus:

ℏ is the conversion rate between T-frame phase budget and S-frame action.
It is not arbitrary, not introduced, and not dimensional bookkeeping.
It is the frame-conversion constant.

6. Worked Numerical Example: n = 1 State

Bohr radius:
$a_0 = 0.529\times 10^{-10}\text{ m}$

Ground state energy:
$E_1 = -13.6\text{ eV}$

This matches the spectroscopic value:

Experimental: −13.598 eV
Theoretical from DFT projection: −13.6 eV

Agreement better than 0.02%.

7. Worked Numerical Example: n = 2 State

Bohr radius:
$r_2 = 4 a_0 = 2.12\times 10^{-10}\text{ m}$

Energy:
$E_2 = -\frac{13.6}{4}\text{ eV} = -3.4\text{ eV}$

This matches:

Experimental: −3.40 eV
DFT projection: −3.4 eV

8. Interpretation Summary

Quantization arises because:

T-frame global phase must close
$\oint d\Theta = 2\pi n$
Projection formalism equates phase with action
$\oint p\,dx = 2\pi n\,\hbar$
Hydrogen energy follows immediately
$E_n = -\frac{13.6\,\text{eV}}{n^2}$

Reciprocal System Research Society

DFT-10a: Quantization as Projection Geometry — Explicit Worked Examples

DFT-10a: Quantization as Projection Geometry — Explicit Worked Examples