DFT-29a: Formal Derivation of BPG Necessity from Topology
Posted: Thu Dec 04, 2025 10:22 pm
This supplement makes precise what was only sketched in DFT-29:
that a Background Phase Geometry (BPG) is not an ad hoc insertion, but a structurally required connection with nontrivial curvature on the T-frame manifold, once we accept global coherence, winding, and compact phase coordinates.
We proceed in five logical steps:
1. Phase manifold and global coherence
We start by formalizing the T-frame phase structure.
Definition 1 (Scalar-motion trajectory).
A scalar-motion trajectory is a map

where Λ is a one-dimensional parameter set (an abstract “motion parameter”) and 𝑀 is the scalar-motion manifold.
Definition 2 (Phase map).
The T-frame phase content is given by a smooth map

where 𝑇𝑘 is a compact k-torus,
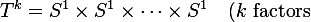.
)
For the present purposes, it suffices to consider the effective one-dimensional phase along a loop, so locally we can work with a single
𝑆1 coordinate 𝜃.
Definition 3 (Pulled-back phase along a loop).
Given a closed trajectory

we define the pulled-back phase

Global coherence assumption.
Coherence in the T-frame means that for any closed loop 𝛾, the phase is single-valued modulo 2𝜋:

\equiv
\Theta_\gamma(\lambda) \ (\mathrm{mod}\ 2\pi).
)
This is precisely what was used in DFT-27 when we wrote

2. Winding number and nontrivial holonomy
Given a map Θ𝛾:𝑆1→𝑆1, we may define its winding number.
Definition 4 (Winding number).
The winding number of Θ𝛾 is
![n[\gamma]
\equiv
\frac{1}{2\pi}
\oint_\gamma d\Theta.](https://reciprocal.systems/cgi-bin/mathtex.cgi?
n[\gamma]
\equiv
\frac{1}{2\pi}
\oint_\gamma d\Theta.
)
This is an integer because Θ𝛾 maps a circle to a circle.
The existence of distinct global winding classes means there are loops 𝛾1,𝛾2 such that
![n[\gamma_1] \ne n[\gamma_2].](https://reciprocal.systems/cgi-bin/mathtex.cgi?
n[\gamma_1] \ne n[\gamma_2].
)
This is equivalent to saying that the phase map realizes a nontrivial element of the fundamental group:
 \cong \mathbb{Z},
)
and that the composition
 \xrightarrow{\ \Theta_*\ } \pi_1(S^1)
)
is nontrivial on some loops. In other words, there exist loops in 𝑀 whose phase cannot be contracted to a constant map in 𝑆1.
This already implies the existence of nontrivial holonomy: traversing a loop in 𝑀 produces a nontrivial phase change in 𝑆1. In geometric language, this is exactly what is meant by nontrivial holonomy around closed curves.
3. Nontrivial holonomy implies a nontrivial connection
To talk about holonomy rigorously, we embed the phase structure in the language of fiber bundles.
Definition 5 (Principal 𝑈(1) bundle for phase).
We consider a principal 𝑈(1) bundle

with structure group 𝑈(1) acting on the fibers. The phase Θ can be understood as a section of an associated bundle or, more concretely, as a local angular coordinate on the fiber.
A connection on this bundle is a 𝑈(1)-valued one-form 𝐴 on 𝑃 which, pulled back along a section, becomes a one-form on 𝑀 representing the “phase connection” in the T-frame:
\, dx^i.
)
The holonomy around a loop 𝛾 is then given by

=
\exp\!\left(
\, i \!\oint_\gamma A
\right)
\in U(1).
)
If the connection is flat, i.e., has vanishing curvature

then locally one can write

for some scalar function 𝜒, and the holonomy becomes

=
\exp\!\left(
\, i \!\oint_\gamma d\chi
\right)
=
\exp\!\left(
i (\chi(\text{endpoint}) - \chi(\text{start}))
\right)
=
1
)
for any contractible loop.
Thus, a flat connection has trivial holonomy around contractible loops.
However, our winding construction says that for certain loops 𝛾,

which yields a nontrivial phase change. In bundle language, we can express the “covariant” phase difference as

=
2\pi n,
\qquad
n \in \mathbb{Z}.
)
exactly as in DFT-27 when we wrote
 = 2\pi n.
)
The upshot is: to accommodate nontrivial winding classes with consistent parallel transport, the connection cannot be globally pure gauge on all of 𝑀. Nontrivial holonomy over noncontractible loops requires either nontrivial bundle topology, or a nontrivial connection (with curvature), or both.
In our context, we are not merely assuming nontrivial topology of 𝑀; we are encoding a global phase structure whose nontrivial winding is physical. This demands a nontrivial connection.
Therefore, a “background phase geometry” in the form of a connection is not optional; it is required by the existence of nontrivial winding plus global coherence.
4. Why the BPG cannot be gauged away
One might ask whether this connection is merely a gauge artifact. Could we perform a global gauge transformation to make 𝐴 vanish everywhere?
A global gauge transformation acts as

and

If the connection were globally pure gauge (i.e., if 𝐴=𝑑𝜒 on all of 𝑀), then in the transformed gauge

However, the winding number is given by
![n[\gamma]
=
\frac{1}{2\pi} \oint_\gamma d\Theta
=
\frac{1}{2\pi} \oint_\gamma d\Theta'.](https://reciprocal.systems/cgi-bin/mathtex.cgi?
n[\gamma]
=
\frac{1}{2\pi} \oint_\gamma d\Theta
=
\frac{1}{2\pi} \oint_\gamma d\Theta'.
)
because the integral of 𝑑𝜒 over a closed loop vanishes. Thus the winding number is gauge invariant.
If we tried to set 𝐴′=0 globally, we would still retain nontrivial winding via Θ′, and the nontrivial holonomy would simply be carried entirely in Θ′ instead of being shared between Θ and 𝐴. But this is only possible if the bundle is topologically trivial and the curvature truly zero.
In the presence of genuinely nontrivial global structure (e.g., nontrivial first Chern class or its T-frame analog), a global gauge where 𝐴′=0 everywhere simply does not exist. Any attempt to construct such a gauge breaks down on transition functions between patches.
Therefore, we have two choices:
5. Why 𝑆𝑈(2)⊕𝑈(1) and not something else?
Up to now we have only used a 𝑈(1)-like structure. Where does 𝑆𝑈(2)⊕𝑈(1) come in?
There are two independent features that must be captured simultaneously:
the electron’s spinor transforms under the fundamental representation of 𝑆𝑈(2), which is the double cover of the spatial rotation group 𝑆𝑂(3). The second points to a 𝑈(1) bundle:
electromagnetic phase is modeled as a 𝑈(1) gauge degree of freedom.
To simultaneously encode spinorial parallel transport and electromagnetic phase in the T-frame, the natural minimal structure group is
 \times U(1),
)
which we denote schematically as 𝑆𝑈(2)⊕𝑈(1) in the DFT exposition.
The BPG is then the background connection on this bundle, with curvature components corresponding to:
Thus, the existence of nontrivial windings for spinor-like and charge-like degrees of freedom, together with the known representation content (spin-½ and electromagnetic phase), naturally points to an 𝑆𝑈(2)×𝑈(1) principal bundle with a nontrivial connection, which is precisely what we mean by the Background Phase Geometry.
Summary of the logical chain
We can now summarize the derivation in compressed logical form:
This completes the formal justification:
BPG is not an empirical patch; it is the minimal geometric structure demanded by the topology, coherence, and representation content of the T-frame phase manifold.
The interpretation presented here should not be understood as a replacement for QED, but rather as a geometric lens through which some of its precision results can be viewed. The Background Phase Geometry is not an alternative to renormalization; it is the geometric structure whose projection renormalization implicitly compensates for. The conventional tools remain unchanged, but their outputs appear to trace the contours of a deeper global coherence. It would be interesting to examine whether similar geometric offsets arise in other settings where projection equivalence is delicate, such as in multiphoton interference, atomic parity mixing, or topological photonic lattices. Whether this background geometry is merely a suggestive analogy or a unifying mathematical structure is a question that seems well-suited for further study.
that a Background Phase Geometry (BPG) is not an ad hoc insertion, but a structurally required connection with nontrivial curvature on the T-frame manifold, once we accept global coherence, winding, and compact phase coordinates.
We proceed in five logical steps:
- Define the phase manifold and global coherence.
- Show that nontrivial winding implies nontrivial holonomy.
- Show that nontrivial holonomy implies a nonflat connection.
- Show that this connection cannot be “gauged away” if winding is to be preserved.
- Show that the symmetry and representation content force an 𝑆𝑈(2)⊕𝑈(1) structure.
1. Phase manifold and global coherence
We start by formalizing the T-frame phase structure.
Definition 1 (Scalar-motion trajectory).
A scalar-motion trajectory is a map
where Λ is a one-dimensional parameter set (an abstract “motion parameter”) and 𝑀 is the scalar-motion manifold.
Definition 2 (Phase map).
The T-frame phase content is given by a smooth map
where 𝑇𝑘 is a compact k-torus,
For the present purposes, it suffices to consider the effective one-dimensional phase along a loop, so locally we can work with a single
𝑆1 coordinate 𝜃.
Definition 3 (Pulled-back phase along a loop).
Given a closed trajectory
we define the pulled-back phase
Global coherence assumption.
Coherence in the T-frame means that for any closed loop 𝛾, the phase is single-valued modulo 2𝜋:
This is precisely what was used in DFT-27 when we wrote
2. Winding number and nontrivial holonomy
Given a map Θ𝛾:𝑆1→𝑆1, we may define its winding number.
Definition 4 (Winding number).
The winding number of Θ𝛾 is
This is an integer because Θ𝛾 maps a circle to a circle.
The existence of distinct global winding classes means there are loops 𝛾1,𝛾2 such that
This is equivalent to saying that the phase map realizes a nontrivial element of the fundamental group:
and that the composition
is nontrivial on some loops. In other words, there exist loops in 𝑀 whose phase cannot be contracted to a constant map in 𝑆1.
This already implies the existence of nontrivial holonomy: traversing a loop in 𝑀 produces a nontrivial phase change in 𝑆1. In geometric language, this is exactly what is meant by nontrivial holonomy around closed curves.
3. Nontrivial holonomy implies a nontrivial connection
To talk about holonomy rigorously, we embed the phase structure in the language of fiber bundles.
Definition 5 (Principal 𝑈(1) bundle for phase).
We consider a principal 𝑈(1) bundle
with structure group 𝑈(1) acting on the fibers. The phase Θ can be understood as a section of an associated bundle or, more concretely, as a local angular coordinate on the fiber.
A connection on this bundle is a 𝑈(1)-valued one-form 𝐴 on 𝑃 which, pulled back along a section, becomes a one-form on 𝑀 representing the “phase connection” in the T-frame:
The holonomy around a loop 𝛾 is then given by
If the connection is flat, i.e., has vanishing curvature
then locally one can write
for some scalar function 𝜒, and the holonomy becomes
for any contractible loop.
Thus, a flat connection has trivial holonomy around contractible loops.
However, our winding construction says that for certain loops 𝛾,
which yields a nontrivial phase change. In bundle language, we can express the “covariant” phase difference as
exactly as in DFT-27 when we wrote
The upshot is: to accommodate nontrivial winding classes with consistent parallel transport, the connection cannot be globally pure gauge on all of 𝑀. Nontrivial holonomy over noncontractible loops requires either nontrivial bundle topology, or a nontrivial connection (with curvature), or both.
In our context, we are not merely assuming nontrivial topology of 𝑀; we are encoding a global phase structure whose nontrivial winding is physical. This demands a nontrivial connection.
Therefore, a “background phase geometry” in the form of a connection is not optional; it is required by the existence of nontrivial winding plus global coherence.
4. Why the BPG cannot be gauged away
One might ask whether this connection is merely a gauge artifact. Could we perform a global gauge transformation to make 𝐴 vanish everywhere?
A global gauge transformation acts as
and
If the connection were globally pure gauge (i.e., if 𝐴=𝑑𝜒 on all of 𝑀), then in the transformed gauge
However, the winding number is given by
because the integral of 𝑑𝜒 over a closed loop vanishes. Thus the winding number is gauge invariant.
If we tried to set 𝐴′=0 globally, we would still retain nontrivial winding via Θ′, and the nontrivial holonomy would simply be carried entirely in Θ′ instead of being shared between Θ and 𝐴. But this is only possible if the bundle is topologically trivial and the curvature truly zero.
In the presence of genuinely nontrivial global structure (e.g., nontrivial first Chern class or its T-frame analog), a global gauge where 𝐴′=0 everywhere simply does not exist. Any attempt to construct such a gauge breaks down on transition functions between patches.
Therefore, we have two choices:
- Deny the physical meaningfulness of global winding classes; or
- Accept a nontrivial connection with background curvature.
5. Why 𝑆𝑈(2)⊕𝑈(1) and not something else?
Up to now we have only used a 𝑈(1)-like structure. Where does 𝑆𝑈(2)⊕𝑈(1) come in?
There are two independent features that must be captured simultaneously:
- Spinorial degrees of freedom (two-valuedness, double cover of 𝑆𝑂(3)).
- Phase coherence of charge-like degrees of freedom (electromagnetic phase).
the electron’s spinor transforms under the fundamental representation of 𝑆𝑈(2), which is the double cover of the spatial rotation group 𝑆𝑂(3). The second points to a 𝑈(1) bundle:
electromagnetic phase is modeled as a 𝑈(1) gauge degree of freedom.
To simultaneously encode spinorial parallel transport and electromagnetic phase in the T-frame, the natural minimal structure group is
which we denote schematically as 𝑆𝑈(2)⊕𝑈(1) in the DFT exposition.
The BPG is then the background connection on this bundle, with curvature components corresponding to:
- The spin-geometry part (related to how spinor windings are embedded), and
The phase-geometry part (related to charge-like phase progression).
Thus, the existence of nontrivial windings for spinor-like and charge-like degrees of freedom, together with the known representation content (spin-½ and electromagnetic phase), naturally points to an 𝑆𝑈(2)×𝑈(1) principal bundle with a nontrivial connection, which is precisely what we mean by the Background Phase Geometry.
Summary of the logical chain
We can now summarize the derivation in compressed logical form:
- Coherent T-frame phases map loops to 𝑆1 with integer winding:
- Nontrivial winding implies nontrivial holonomy in a principal 𝑈(1) bundle over 𝑀.
- Nontrivial holonomy implies that the connection cannot be globally trivial (pure gauge) on all of 𝑀; there must be nontrivial global bundle/connection structure. In the BPG picture this is realized as a fixed background connection with nonvanishing curvature.
- This connection cannot be globally gauged away without destroying the winding structure; it is structurally required, not emergent.
- Spinorial and charge-like windings together require an 𝑆𝑈(2)×𝑈(1) principal bundle. The corresponding fixed connection and curvature constitute the BPG.
This completes the formal justification:
BPG is not an empirical patch; it is the minimal geometric structure demanded by the topology, coherence, and representation content of the T-frame phase manifold.
The interpretation presented here should not be understood as a replacement for QED, but rather as a geometric lens through which some of its precision results can be viewed. The Background Phase Geometry is not an alternative to renormalization; it is the geometric structure whose projection renormalization implicitly compensates for. The conventional tools remain unchanged, but their outputs appear to trace the contours of a deeper global coherence. It would be interesting to examine whether similar geometric offsets arise in other settings where projection equivalence is delicate, such as in multiphoton interference, atomic parity mixing, or topological photonic lattices. Whether this background geometry is merely a suggestive analogy or a unifying mathematical structure is a question that seems well-suited for further study.