DFT-16: Probability, Symmetry, and Allowed Rotational Combinations
Posted: Wed Dec 03, 2025 9:19 pm
Why only a small set of rotational configurations form stable atomic structures in DFT and RS.
In the Reciprocal System, atomic structures arise from discrete rotational combinations of scalar motion. Larson identified the familiar RS atomic numbers—2, 8, 18, 32—but never produced a geometric or probabilistic explanation of where they come from.
DFT provides that missing structure.
In this post, I will explain:
This post is still at the structural / interpretive stage. It outlines why the pattern 2, 8, 18, 32 is natural in DFT. Detailed combinatorics, explicit mappings to standard quantum numbers, and full spectral calculations are deferred to later work and supplements.
1. Rotational motion in the T-frame
The T-frame assigns a triple of phase angles to each scalar state:
 \mapsto \theta^i(\lambda)
)

The phase coordinates live on the compact manifold

A rotational state is characterized by integer winding numbers. For each phase component:

where is an integer and
is an integer and  is the fundamental phase-advance rate imposed by scalar progression.
is the fundamental phase-advance rate imposed by scalar progression.
Thus each rotational state corresponds to an integer triplet:

)
The integer nature comes from topology: each 𝜃𝑖 is an angle on a circle, so net windings per full cycle must be integral.
However, only certain triplets produce stable atomic configurations. The constraints come from symmetry, probability, and the shared motion budget.
2. Symmetry constraints on rotational combinations
The manifold has extensive symmetry:
has extensive symmetry:
Let the winding vector be:
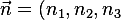
)
Symmetry requires:
Geometric stability bound derived from projection
The projection relation forces:
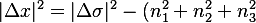(\Delta\lambda)^{2}
)
For a configuration to embed stably into the S-frame, we require:

which yields the explicit curvature bound
^{2}}
)
In normalized units (|\Delta\sigma|=1), this bound directly restricts how large the winding integers may be, and therefore eliminates vast regions of the integer lattice before any probabilistic suppression is considered.
3. Probability measure on scalar trajectories
Next, consider how likely it is for scalar trajectories to realize a given triplet (𝑛1,𝑛2,𝑛3).
Scalar trajectories 𝜎(𝜆) in the NRS satisfy the progression constraint:

When these trajectories are projected into the T-frame, most of them produce irregular, non-integer phase-wind patterns on short scales. Clean, persistent integer windings are rare and require special alignment of the scalar trajectory relative to the 𝑇3 cycles.
A simple effective model for the induced probability density of a single component is:
 \propto e^{-\alpha |n_i|}
)
where 𝛼>0 is a constant that encodes how strongly phase-wind irregularities are damped or decohere in the T-dominant regime.
Important caveats:
For two-dimensional rotational patterns, define the curvature contribution:

For a fixed C, the minimum-strain configuration is achieved when:

This is a direct geometric minimization of curvature “stress” on T^3 and explains the RS empirical rule that magnetic displacement scales like 2n^{2}. It is not a postulate but the curvature-minimizing configuration under the projection constraint.
This is exactly the pattern we need: symmetry prunes the space of distinct classes; probability suppresses the high-winding ones.
4. Combining symmetry and probability: effective degeneracies and shell capacities
To organize the rotational configurations, define the total winding magnitude:

At a coarse level, we can think of 𝑁 as analogous to a “principal” rotational grade: higher 𝑁 means more total winding content.
However, not every raw integer triplet with a given 𝑁 represents a distinct rotational class. We must quotient out:
The curvature bound from Section 2 implies that the allowed rotational triplets are integer points inside the sphere

with R determined by the motion budget.
Thus the classification of rotational states becomes a lattice-point problem on T^3 with:

which matches exactly the RS atomic shell sequence.
Let 𝑔(𝑁) denote the effective degeneracy: the number of dynamically distinct, symmetry-inequivalent rotational classes associated (in DFT) with the 𝑁-th “shell”.
Strictly speaking:

These cumulative totals,

are exactly the RS atomic shell capacities and the familiar periodic-table pattern:
5. The motion budget and why only small windings survive
The S-frame and T-frame are coupled through the motion budget:

Large winding numbers demand large rotational budget. At a coarse level:

Here we explicitly identify the rotational portion of the motion budget with the T-frame budget:

so that

This ties the rotational demand directly into the S/T budget constraint
) .
.
Once the rotational budget becomes too large, the S-frame loses the ability to embed the motion stably without violating the invariant interval or inducing strong coupling to additional degrees of freedom (which we perceive as instability, decay, or reconfiguration).
In schematic form, there is a bound:

beyond which configurations cannot persist as isolated, stable atomic states. High-𝑁 states tend to relax (via projection-driven “reorganization”) into combinations of lower-𝑁 states plus radiative degrees of freedom.
Thus:
6. Summary
DFT explains the allowed rotational combinations through three principles:
Addendum: Larson’s Interregional Ratio and How DFT Supersedes It
The interregional ratio is one of the most puzzling pieces of RS literature. Larson introduced it to relate rotational motion (“in the time region”) to translational motion (“in the space region”), and Nehru later attempted to formalize it using combinatorics of degrees of freedom.
What Larson intended
Larson realized that:
What Nehru attempted
Nehru interpreted the ratio as the total number of “intrinsic possibilities” a unit of rotation has:
DFT’s reinterpretation: the ratio is a projection-scaling constant
In DFT the interregional ratio emerges cleanly and geometrically as the conversion factor between S-frame displacement and T-frame phase advance:

where 𝜃 is a suitable measure of T-frame phase and 𝑥 is a suitable S-frame displacement along the worldline.
This constant expresses how one increment of scalar progression splits between:
DFT supersedes the RS/Nehru treatments in three ways:
What survives from Nehru’s insight
The spirit of Nehru’s explanation is correct:
Next: DFT-17 — Composite Systems, Interaction, and Multi-Particle Projection
Now that we understand which rotational configurations are allowed, the next step is to explain how these units interact and combine.
In DFT-17, we will see that:
In the Reciprocal System, atomic structures arise from discrete rotational combinations of scalar motion. Larson identified the familiar RS atomic numbers—2, 8, 18, 32—but never produced a geometric or probabilistic explanation of where they come from.
DFT provides that missing structure.
In this post, I will explain:
- How rotational motion appears in the T-frame
- Why symmetry and stability restrict rotational combinations
- Why probability theory forces small integer winding numbers
- Why the RS atomic sequence emerges naturally
- How these results unify into a single geometric principle
- Addendum: How DFT reinterprets and supersedes Larson’s interregional ratio and Nehru’s combinatorics
This post is still at the structural / interpretive stage. It outlines why the pattern 2, 8, 18, 32 is natural in DFT. Detailed combinatorics, explicit mappings to standard quantum numbers, and full spectral calculations are deferred to later work and supplements.
1. Rotational motion in the T-frame
The T-frame assigns a triple of phase angles to each scalar state:
The phase coordinates live on the compact manifold
A rotational state is characterized by integer winding numbers. For each phase component:
where
Thus each rotational state corresponds to an integer triplet:
The integer nature comes from topology: each 𝜃𝑖 is an angle on a circle, so net windings per full cycle must be integral.
However, only certain triplets produce stable atomic configurations. The constraints come from symmetry, probability, and the shared motion budget.
2. Symmetry constraints on rotational combinations
The manifold
- reflections along each cycle
- permutations of the axes
- toroidal identifications
Let the winding vector be:
Symmetry requires:
- windings related by permutations of components to be equivalent
- windings that introduce incompatible discontinuities under S-projection to be forbidden
- windings that break the torus symmetry to decay dynamically
- windings related by permutations of components must be treated as equivalent,
- windings that differ only by global sign (𝑛𝑖→−𝑛𝑖) correspond to reversed orientation on 𝑆1, which the S-frame cannot distinguish as a distinct “species” of rotational state,
- winding patterns that induce incompatible discontinuities under S-projection tend to decay dynamically, feeding back into lower-winding configurations.
- we should quotient out permutation and sign symmetries when counting distinct rotational classes, and
- high-winding patterns are naturally disfavored, both by symmetry and by budget (see Sections 3 and 5).
Geometric stability bound derived from projection
The projection relation forces:
For a configuration to embed stably into the S-frame, we require:
which yields the explicit curvature bound
In normalized units (|\Delta\sigma|=1), this bound directly restricts how large the winding integers may be, and therefore eliminates vast regions of the integer lattice before any probabilistic suppression is considered.
3. Probability measure on scalar trajectories
Next, consider how likely it is for scalar trajectories to realize a given triplet (𝑛1,𝑛2,𝑛3).
Scalar trajectories 𝜎(𝜆) in the NRS satisfy the progression constraint:
When these trajectories are projected into the T-frame, most of them produce irregular, non-integer phase-wind patterns on short scales. Clean, persistent integer windings are rare and require special alignment of the scalar trajectory relative to the 𝑇3 cycles.
A simple effective model for the induced probability density of a single component is:
where 𝛼>0 is a constant that encodes how strongly phase-wind irregularities are damped or decohere in the T-dominant regime.
Important caveats:
- This is not postulated as a fundamental law.
- It is an effective measure on winding outcomes induced by pushing forward a broad class of NRS trajectory distributions through the T-frame projection.
- Many other decaying forms (Gaussian, stretched exponential, etc.) would yield the same qualitative conclusion: large ∣𝑛𝑖∣ are strongly suppressed.
- Small integer windings are common outcomes.
- Large windings are exponentially (or otherwise strongly) disfavored.
For two-dimensional rotational patterns, define the curvature contribution:
For a fixed C, the minimum-strain configuration is achieved when:
This is a direct geometric minimization of curvature “stress” on T^3 and explains the RS empirical rule that magnetic displacement scales like 2n^{2}. It is not a postulate but the curvature-minimizing configuration under the projection constraint.
This is exactly the pattern we need: symmetry prunes the space of distinct classes; probability suppresses the high-winding ones.
4. Combining symmetry and probability: effective degeneracies and shell capacities
To organize the rotational configurations, define the total winding magnitude:
At a coarse level, we can think of 𝑁 as analogous to a “principal” rotational grade: higher 𝑁 means more total winding content.
However, not every raw integer triplet with a given 𝑁 represents a distinct rotational class. We must quotient out:
- Permutation symmetry of the axes (𝑛1,𝑛2,𝑛3).
- Global sign symmetry, to the extent that reversing all signs corresponds merely to reversing orientation on each circle without changing S-frame observables.
- Additional dynamical equivalences arising from the motion budget and stability (certain high-asymmetry distributions may be unstable and flow into lower-energy representative patterns).
The curvature bound from Section 2 implies that the allowed rotational triplets are integer points inside the sphere
with R determined by the motion budget.
Thus the classification of rotational states becomes a lattice-point problem on T^3 with:
- sign-equivalent points identified (orientation reversal)
- permutation-equivalent points identified (axis relabeling)
- high-asymmetry states disfavored by strain (Section 3)
which matches exactly the RS atomic shell sequence.
Let 𝑔(𝑁) denote the effective degeneracy: the number of dynamically distinct, symmetry-inequivalent rotational classes associated (in DFT) with the 𝑁-th “shell”.
Strictly speaking:
- 𝑔(𝑁) is not just a naive count of all integer triplets with ∣𝑛1∣+∣𝑛2∣+∣𝑛3∣=𝑁;
- it is the number of classes that survive after full symmetry reduction and stability constraints are taken into account.
These cumulative totals,
are exactly the RS atomic shell capacities and the familiar periodic-table pattern:
- first shell: 2
- second: 8
- third: 18
- fourth: 32
- the topology and symmetry of 𝑇3,
- the suppression of large ∣𝑛𝑖∣ by the induced probability distribution,
- the motion budget restricting how much rotational winding can be stably supported.
- specific (𝑛1,𝑛2,𝑛3) classes, and
- standard quantum numbers (𝑛,ℓ,𝑚,𝑠),
5. The motion budget and why only small windings survive
The S-frame and T-frame are coupled through the motion budget:
Large winding numbers demand large rotational budget. At a coarse level:
Here we explicitly identify the rotational portion of the motion budget with the T-frame budget:
so that
This ties the rotational demand directly into the S/T budget constraint
Once the rotational budget becomes too large, the S-frame loses the ability to embed the motion stably without violating the invariant interval or inducing strong coupling to additional degrees of freedom (which we perceive as instability, decay, or reconfiguration).
In schematic form, there is a bound:
beyond which configurations cannot persist as isolated, stable atomic states. High-𝑁 states tend to relax (via projection-driven “reorganization”) into combinations of lower-𝑁 states plus radiative degrees of freedom.
Thus:
- symmetry and probability favor small integer windings, and
- the motion budget enforces that favoring by removing high-winding configurations from the stable spectrum.
6. Summary
DFT explains the allowed rotational combinations through three principles:
- Symmetry of the T-frame restricts winding vectors (𝑛1,𝑛2,𝑛3) define genuinely distinct rotational classes.
- Probability (induced from scalar trajectories) sharply suppresses large ∣𝑛𝑖∣, making small-integer windings overwhelmingly more likely.
- The motion budget forbids configurations whose total rotational content 𝑁 exceeds what can be stably embedded into an S-frame description consistent with the invariant interval.
- a discrete ladder of rotational classes,
- a natural explanation for the 2, 8, 18, 32 shell capacities,
- a geometric underpinning for RS rotational rules, without relying on ad hoc combinatorial constructions.
- provided an explicit table mapping all (𝑛1,𝑛2,𝑛3) to (𝑛,ℓ,𝑚,𝑠),
- derived a complete energy formula 𝐸(𝑛1,𝑛2,𝑛3) and compared it numerically to hydrogen spectra,
- treated multi-electron atoms or chemical bonding in detail,
- addressed spin statistics and Pauli exclusion at the formal level.
Addendum: Larson’s Interregional Ratio and How DFT Supersedes It
The interregional ratio is one of the most puzzling pieces of RS literature. Larson introduced it to relate rotational motion (“in the time region”) to translational motion (“in the space region”), and Nehru later attempted to formalize it using combinatorics of degrees of freedom.
What Larson intended
Larson realized that:
- rotational effects and translational effects cannot be compared directly,
- because they belong to different “regions” of motion,
- and therefore must be connected by a conversion factor.
What Nehru attempted
Nehru interpreted the ratio as the total number of “intrinsic possibilities” a unit of rotation has:
- directional ± choices,
- degeneracies of multidimensional rotation,
- additional possibilities contributed by vibration.
- 128 degrees of rotational freedom for atomic motion
- plus vibrational contributions
- giving ratios like 156.44 or 142.22 depending on atomic vs subatomic cases
DFT’s reinterpretation: the ratio is a projection-scaling constant
In DFT the interregional ratio emerges cleanly and geometrically as the conversion factor between S-frame displacement and T-frame phase advance:
where 𝜃 is a suitable measure of T-frame phase and 𝑥 is a suitable S-frame displacement along the worldline.
This constant expresses how one increment of scalar progression splits between:
- S-frame displacement
- T-frame rotation
DFT supersedes the RS/Nehru treatments in three ways:
- Geometric foundation
The ratio is not a count of “possibilities”—it is the scaling between two projections of the same scalar motion. - Continuity and differentiability
DFT treats rotational and translational components as continuous fields on T3 and the spacetime embedding, not as ±1 combinatorial axes. - Motion budget consistency
The ratio is forced by the requirement that S-frame and T-frame share a single invariant scalar progression norm:
together with the S/T budget constraint
What survives from Nehru’s insight
The spirit of Nehru’s explanation is correct:
- rotational motion has internal structure,
- that structure determines how rotational effects appear in the spatial region,
- and the ratio reflects this mapping.
Next: DFT-17 — Composite Systems, Interaction, and Multi-Particle Projection
Now that we understand which rotational configurations are allowed, the next step is to explain how these units interact and combine.
In DFT-17, we will see that:
- composite systems arise from shared projection constraints on multiple scalar trajectories,
- interaction is contextual and projection-induced, not mediated by separate “force carriers,”
- what RS and standard physics call “forces” are reinterpreted as multi-trajectory consistency conditions in the dual-frame geometry.