At the end of the previous entry, I wrote that we would introduce a new direction in the mathematical approach of our RSt. I've already written about a new scalar math and introduced the idea of three units of numbers or three number systems based on sqrt of 1, 2 and 3. The genesis of this idea and others that follow stems from the 3d stack of 8, 1-unit cubes, or the 2x2x2 stack of cubes we call Larson's cube (LC).
The fact that the 3d geometric figure of the LC perfectly corresponds to the numbers of the binomial expansion of the tetraktys reveals a deep and fundamental connection, or union, of numbers and geometry. It's hard to overestimate the significance of this discovery, as the pursuit of such a union has driven the historical development of traditional mathematics, from ancient times. I've written much about this on my website at lrcphysics.com.
Here, though, I want to show how the math of the LC, in the form of the binomial expansion of the Tetraktys, should permit us to calculate the values of the LRC's RSt and thus the 1d, 2d and 3d properties of the S|T combos, which should, if valid, yield the magnitudes of the observed properties of the physical entities, which correspond to these various combos.
The key is understanding the expansion, or progression of the scale, or size, of the oscillating LC, since such an expansion corresponds to the sum of all its multi-dimensional scalar motion. To understand this, we must recognize that each physical dimension has two "directions." In the case of the unit LC, we can see that multiplying each dimension by the corresponding coefficient of that dimension, yields the correct number of dimensional units for a given dimension:
Recall that there is 1 0d point, 3 1d lines, 3 2d planes and 1 3d volume in the LC, and that these numbers are identical to the 1 3 3 1 sequence of numbers of the 4th line of the binomial expansion of the Tetraktys (BET). So, we can write this as:
10 x 1 point, 11 x 3 lines, 12 x 3 planes and 13 x 1 volume, or
10 (1mp) + 11 (3dp) + 12 (3qp) + 13 (1op) = 1(1) + 1(3x2) + 1(3x4) + 1(1x8) = 1+6+12+8 = 27 poles, where mp = monopole, dp = dipole, qp = quadrupole and op = octopole.
This is the multi-pole sum of the unit LC. So, to sum multiple units of the LC, we simply sum the coefficients of each dimension times the number of poles in that dimension:
n0(1mp) + n1(3dp) + n2(3qp) + n3(1op), or
n0(1) + n1(6) + n2(12) + n3(8).
On this basis, the progression of the LC, in terms of poles is, 27, 125, 343, 729, or
33, 53, 73, …(2n+1)3, n = 1, 2, 3, …∞
With this much understood, we can proceed to calculate the multi-dimensional magnitudes of the S|T combos. We have long since shown that summing the 1d numbers of the fundamental S|T combo, 1/2 + 1/1 + 2/1 = 4|4 num into the numbers of the triple combo, calculates the neutrino number, enabling us to calculate all the combos corresponding to the quarks and leptons of the first family of the LST's standard model of particle physics. For example, in the material sector:
Electron = 3(6|6) = 18|18;
Anti-Up = (2(6|6) + 4|4 = 12|12 + 4|4 = 16|16;
Down = ((2(4|4) +6|6 = 8|8 + 6|6 = 14|14;
Neutrino = 3(4|4) = 12|12;
Anti-Down = ((2(4|4) +6|6 = 8|8 + 6|6 = 14|14;
Up = (2(6|6) + 4|4 = 12|12 + 4|4 = 16|16;
Positron = 3(6|6) = 18|18;
with the inverse of these corresponding to the cosmic sector of the RST universe.
Combining these into the proton, neutron and helium atom entities, all the 1d charges work out perfectly, corresponding to the electrical properties of the observed entities, even in the beta decay process. However, these 1d numbers are not suitable to calculate the 2d and 3d magnitudes of the combos. We need to be able to calculate with 2d and 3d numbers to do this.
Of course, the vector mathematics of the LST are totally unsuited for this purpose. We must have a new scalar mathematics to calculate the multi-dimensional scalar magnitudes of the S|T combos, and I have shown why this is so on the LRC website. It's quite a story, but it's necessary to understand it, if one is to comprehend what we mean, when we refer to multi-dimensional scalar numbers and magnitudes.
Once it's understood how the scalar motion of an oscillating volume can form the basis for a multi-dimensional scalar mathematics, capable of describing the multi-dimensional magnitudes of scalar motion in various combinations, just as an oscillating vector motion can be used as the basis for multi-dimensional vector mathematics, describing magnitudes of vector motion, a whole new world of possibilities beckons us forward.
Hopefully, it's a valid world that can be shown to correspond to magnitudes of observed properties of matter, but, of course, there's no guarantee. It may turn out to be an exercise in futility, but I think it's worthwhile to explore it and see where it leads.
More next time.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
The idea that multi-dimensional scalars exist isn't in question. They do, even though the idea may seem preposterous to LST mathematicians and physicists. However, that's only because they've yet to recognize scalar motion and the reciprocity of space and time, as shown by Dewey Larson.
Multi-dimensional scalar motion is clearly evident, when we consider an oscillating volume. Such a volume has 0, 1 and 2 dimensional components, as well as a three-dimensional volume and it's clear that they can all be identified mathematically as well as geometrically. The mathematics of the oscillating volume is defined by the multi-dimensional units of Larson's cube, the 2x2x2 stack of 1-unit cubes, in which the radius of the inner volume, which is just contained by the stack, is an integer magnitude and the radius of the outer volume, which just contains the stack, is a non-integer magnitude.
While this may not appear to be very useful at first, I think it will turn out to be very useful eventually, since the ratios between the radii, areas and volumes of the two balls are integral magnitudes. We will explore those magnitudes later, but first we need to understand that the way they arise is fundamental, and this bids us to ponder the theoretical and philosophical implications.
Recall that in the previous post, I showed the startling correspondence between the tetraktys and the LC. We saw how, when the binomial expansion of the tetraktys (BET) is regarded as the expansion of two "directions" in each of three physical dimensions, the result is the mathematical equivalence of the unit LC's geometry. That is, the numerical expansion of the fourth line of the tetraktys,
1+3+3+1,
is equivalent to the geometric expansion of the LC, the 2x2x2 stack of unit cubes, since the LC can be considered to consists of
1 0d point, 3 1d lines, 3 2d planes and 1 3d volume.
As explained in my previous post, when we expand the LC in the two "directions" of each of these dimensions, we can write the expansion of the multiple dimensions in terms of a sum of multi-poles:
10(1mp) + 11(3dp) + 12(3qp) + 13(1op) = 1(1) + 1(3x2) + 1(3x4) + 1(1x8) = 1+6+12+8 = 27 poles,
or, more generally,
n0(1mp) + n1(3dp) + n2(3qp) + n3(1op) = (2n +1)3 poles, n = 1, 2, 3, ...∞. [1]
where mp = monopole, dp = dipole, qp = quadrupole and op = octopole.
Of course, nature doesn't expand by these integer numbers of cubes with their right angles, but by the non-integer geometric magnitudes of balls, with their respective radii, and, as my earlier analysis has shown, there are three of these found in the LC:
√1, √2, and √3.
Consequently, the expansion of the LC, in terms of the numbers of the tetraktys, can be thought of as the geometric expansion of the 1d, 2d and 3d non-integer magnitudes, as well as the 1d, 2d and 3d integer magnitudes of [1], recalling that numbers have, as magnitudes do, three properties: magnitude, dimension and "direction."
Since each dimension has two "directions" in which magnitude can exist, the binomial expansion of the tetraktys enables us to identify it with the LC, up to its three, non-zero, dimensions. Beyond that, however, the powers of two that we find in Pascal's triangle, while exhibiting some of the properties of the LC expansion, loses its dimensional correlation with the LC. It is the expansion of the 3d level of the triangle that constitutes what we might call a 3d scalar number, and we can expand its integer magnitudes as shown in [1] above, or its non-integer magnitudes, as I will show now.
To do this, we simply multiply our 3d number, which we will designate with an uppercase R, by n, where n = 1, 2, 3, ...∞:
1 x R = 1mp+3dp+3qp+1op = (1x20)+(3x21)+(3x22)+(1x23) = 1+6+12+8 = 27;
2 x R = 2(1+6+12+8) = 2+12+24+16 = 54;
3 x R = 3(1+6+12+8) = 3+18+36+24 = 81;
.
.
.
n x R = n(1+6+12+8) = n+6n+12n+8n = 27n.
The dimensions of the terms of the expanded number ascend left to right, from 0 to 3, so there are n 0-dimensional units, followed by 6n 1-dimensional, 12n 2-dimensional, and 8n 3-dimensional units in the number. The magnitude and dimension of these units, ud, are:
u1 = √1,
u2 = √2,
u3 = √3,
as appropriate for each non-zero dimension:
n x Rud = 1n+6nu1+12nu2+8nu3 = 27nud
It's important to understand that the subscript number of the units, while identical to the exponential number of respective poles in each term, is an actual magnitude of the corresponding unit, so that the 1d unit (√1) is multiplied by the 1d coefficient (6n), the 2d unit (√2), by the 2d coefficient (12n), and the 3d unit (√3), by the 3d coefficient (8n).
Presumably, on this basis, we can calculate the units of n-dimensional motion in a given reciprocal number (RN) = n(1/2+1/1+2/1) = n(4|4). The procedure we will use requires us to take the ratio of various geometric quantities, based on these 3d numbers, as I will discuss next time.
Multi-dimensional scalar motion is clearly evident, when we consider an oscillating volume. Such a volume has 0, 1 and 2 dimensional components, as well as a three-dimensional volume and it's clear that they can all be identified mathematically as well as geometrically. The mathematics of the oscillating volume is defined by the multi-dimensional units of Larson's cube, the 2x2x2 stack of 1-unit cubes, in which the radius of the inner volume, which is just contained by the stack, is an integer magnitude and the radius of the outer volume, which just contains the stack, is a non-integer magnitude.
While this may not appear to be very useful at first, I think it will turn out to be very useful eventually, since the ratios between the radii, areas and volumes of the two balls are integral magnitudes. We will explore those magnitudes later, but first we need to understand that the way they arise is fundamental, and this bids us to ponder the theoretical and philosophical implications.
Recall that in the previous post, I showed the startling correspondence between the tetraktys and the LC. We saw how, when the binomial expansion of the tetraktys (BET) is regarded as the expansion of two "directions" in each of three physical dimensions, the result is the mathematical equivalence of the unit LC's geometry. That is, the numerical expansion of the fourth line of the tetraktys,
1+3+3+1,
is equivalent to the geometric expansion of the LC, the 2x2x2 stack of unit cubes, since the LC can be considered to consists of
1 0d point, 3 1d lines, 3 2d planes and 1 3d volume.
As explained in my previous post, when we expand the LC in the two "directions" of each of these dimensions, we can write the expansion of the multiple dimensions in terms of a sum of multi-poles:
10(1mp) + 11(3dp) + 12(3qp) + 13(1op) = 1(1) + 1(3x2) + 1(3x4) + 1(1x8) = 1+6+12+8 = 27 poles,
or, more generally,
n0(1mp) + n1(3dp) + n2(3qp) + n3(1op) = (2n +1)3 poles, n = 1, 2, 3, ...∞. [1]
where mp = monopole, dp = dipole, qp = quadrupole and op = octopole.
Of course, nature doesn't expand by these integer numbers of cubes with their right angles, but by the non-integer geometric magnitudes of balls, with their respective radii, and, as my earlier analysis has shown, there are three of these found in the LC:
√1, √2, and √3.
Consequently, the expansion of the LC, in terms of the numbers of the tetraktys, can be thought of as the geometric expansion of the 1d, 2d and 3d non-integer magnitudes, as well as the 1d, 2d and 3d integer magnitudes of [1], recalling that numbers have, as magnitudes do, three properties: magnitude, dimension and "direction."
Since each dimension has two "directions" in which magnitude can exist, the binomial expansion of the tetraktys enables us to identify it with the LC, up to its three, non-zero, dimensions. Beyond that, however, the powers of two that we find in Pascal's triangle, while exhibiting some of the properties of the LC expansion, loses its dimensional correlation with the LC. It is the expansion of the 3d level of the triangle that constitutes what we might call a 3d scalar number, and we can expand its integer magnitudes as shown in [1] above, or its non-integer magnitudes, as I will show now.
To do this, we simply multiply our 3d number, which we will designate with an uppercase R, by n, where n = 1, 2, 3, ...∞:
1 x R = 1mp+3dp+3qp+1op = (1x20)+(3x21)+(3x22)+(1x23) = 1+6+12+8 = 27;
2 x R = 2(1+6+12+8) = 2+12+24+16 = 54;
3 x R = 3(1+6+12+8) = 3+18+36+24 = 81;
.
.
.
n x R = n(1+6+12+8) = n+6n+12n+8n = 27n.
The dimensions of the terms of the expanded number ascend left to right, from 0 to 3, so there are n 0-dimensional units, followed by 6n 1-dimensional, 12n 2-dimensional, and 8n 3-dimensional units in the number. The magnitude and dimension of these units, ud, are:
u1 = √1,
u2 = √2,
u3 = √3,
as appropriate for each non-zero dimension:
n x Rud = 1n+6nu1+12nu2+8nu3 = 27nud
It's important to understand that the subscript number of the units, while identical to the exponential number of respective poles in each term, is an actual magnitude of the corresponding unit, so that the 1d unit (√1) is multiplied by the 1d coefficient (6n), the 2d unit (√2), by the 2d coefficient (12n), and the 3d unit (√3), by the 3d coefficient (8n).
Presumably, on this basis, we can calculate the units of n-dimensional motion in a given reciprocal number (RN) = n(1/2+1/1+2/1) = n(4|4). The procedure we will use requires us to take the ratio of various geometric quantities, based on these 3d numbers, as I will discuss next time.
Re: Meeting a Terrific Challenge
The most enduring challenge that Western science has faced down through the centuries, since the days of the brilliant Greeks, like Pythagoras and Euclid, is the fact that there are geometric magnitudes for which there are no corresponding numbers. It is the same challenge facing the modern LST community today: The integer numbers of quantum physics are irreconcilable with the geometric magnitudes of general relativity, creating the same kind of impasse the ancients faced. Believe it or not, digital approximation to analog magnitudes is still incomplete, in spite of the spectacular sight of 4k video and other technological achievements of the 21st century.
Perhaps Kronecker was right, after all, even though the world has followed Dedekind cuts and Cantor sets into the realm of real numbers, notwithstanding the objections of philosophers. Larson assumes Kronecker was right: "God made the integers, all the rest is the work of man," as he has taken a revolutionary approach to answering the question of how our analog world emerges from God's integers, even though that was not his intention, per se.
As it turns out, though, the 3d scalar expansion of numbers can be in-separately connected to the 3d scalar expansion of geometry, by recognizing the identity of the tetraktys and LC, uniting the magnitudes of numbers, with those of geometry, if I'm not mistaken.
What makes this possible is the fact that the ratio of the irrational numbers in the expanding LC, such as π, cancel out in these ratios, leaving only integers, or the square roots of integers. Consequently, the expanding cubes of the LC, though not corresponding to the 2d areas and 3d volumes of physical expansion, or progression, directly, nevertheless determine the boundaries of these associated 2d areas and 3d volumes, and the ratio of these turns out to be integer magnitudes, or their square roots, in terms of a given 2d or 3d unit.
For example, the ratio of the unit 3d volume with the radius square root of 3, to the surface area of the 2d sphere, with the radius square root of 2, is 1, 2, 3 ...n, in units of √3. The ratio of the same volume to the circle area of the 2d volume (its cross section) is 2, 4, 6, ...2n, again in units of √3.
Given that the LC defines three volumes, areas and radii, there are lots of combinations to consider, and I will try to deal with these systematically, in due course, but first the issue of how these magnitudes combine has to be addressed.
Recall that in the previous post, it was shown how the numerical expansion of the LC stack of 8 one-unit cubes can be calculated using the numbers of the fourth line (dimension) of the tetraktys, as shown in the table below:
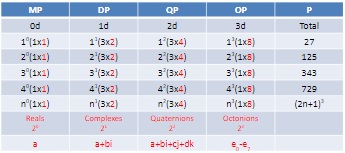
This expansion of the geometric stack via its correspondence to the tetraktys may seem non-intuitive at first glance, because, when we think of a stack of 8 cubes added to another stack of 8 cubes, we intuitively think we should have 8+8 = 16 cubes.
However, when we are adding 23 + n3, the sum is equal to (2+n)3, not 8+n3. In the case of 1 stack +1 stack, for instance, we have:
(2x2x2) + (2x2x2) = 23 + 23 = 43 = 64 cubes, not 8 + 8 = 16 cubes.
With this much understood, we can calculate the magnitudes of the volumes defined by the magnitude of a given stack and the respective radii determined by that stack. We just use the multi-dimensional number line shown in the table below:
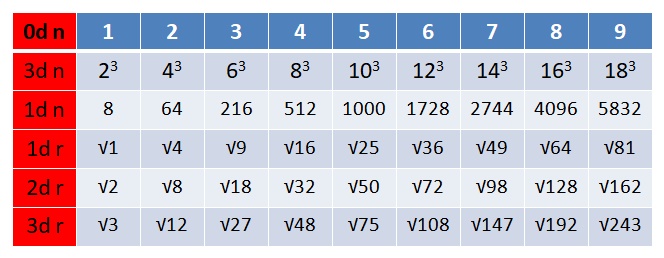
The chart omits the 2d number line, but it shows the progression of all three radii, which we can use to calculate the magnitudes of the volumes and areas of each of the three balls of any given LC combo and their ratios, and this capability should enable us to calculate the magnitude of the 2d and 3d scalar motion associated with a given RN, n(1/2+1/1+2/1).
If this is the correct approach, it ought to enable us to calculate the 2d and 3d magnitudes of a given S|T combo, such as those found in the LRC's version of the LST's standard model of particle physics, and thereby hopefully match their observed magnetic and mass properties.
Perhaps Kronecker was right, after all, even though the world has followed Dedekind cuts and Cantor sets into the realm of real numbers, notwithstanding the objections of philosophers. Larson assumes Kronecker was right: "God made the integers, all the rest is the work of man," as he has taken a revolutionary approach to answering the question of how our analog world emerges from God's integers, even though that was not his intention, per se.
As it turns out, though, the 3d scalar expansion of numbers can be in-separately connected to the 3d scalar expansion of geometry, by recognizing the identity of the tetraktys and LC, uniting the magnitudes of numbers, with those of geometry, if I'm not mistaken.
What makes this possible is the fact that the ratio of the irrational numbers in the expanding LC, such as π, cancel out in these ratios, leaving only integers, or the square roots of integers. Consequently, the expanding cubes of the LC, though not corresponding to the 2d areas and 3d volumes of physical expansion, or progression, directly, nevertheless determine the boundaries of these associated 2d areas and 3d volumes, and the ratio of these turns out to be integer magnitudes, or their square roots, in terms of a given 2d or 3d unit.
For example, the ratio of the unit 3d volume with the radius square root of 3, to the surface area of the 2d sphere, with the radius square root of 2, is 1, 2, 3 ...n, in units of √3. The ratio of the same volume to the circle area of the 2d volume (its cross section) is 2, 4, 6, ...2n, again in units of √3.
Given that the LC defines three volumes, areas and radii, there are lots of combinations to consider, and I will try to deal with these systematically, in due course, but first the issue of how these magnitudes combine has to be addressed.
Recall that in the previous post, it was shown how the numerical expansion of the LC stack of 8 one-unit cubes can be calculated using the numbers of the fourth line (dimension) of the tetraktys, as shown in the table below:

This expansion of the geometric stack via its correspondence to the tetraktys may seem non-intuitive at first glance, because, when we think of a stack of 8 cubes added to another stack of 8 cubes, we intuitively think we should have 8+8 = 16 cubes.
However, when we are adding 23 + n3, the sum is equal to (2+n)3, not 8+n3. In the case of 1 stack +1 stack, for instance, we have:
(2x2x2) + (2x2x2) = 23 + 23 = 43 = 64 cubes, not 8 + 8 = 16 cubes.
With this much understood, we can calculate the magnitudes of the volumes defined by the magnitude of a given stack and the respective radii determined by that stack. We just use the multi-dimensional number line shown in the table below:

The chart omits the 2d number line, but it shows the progression of all three radii, which we can use to calculate the magnitudes of the volumes and areas of each of the three balls of any given LC combo and their ratios, and this capability should enable us to calculate the magnitude of the 2d and 3d scalar motion associated with a given RN, n(1/2+1/1+2/1).
If this is the correct approach, it ought to enable us to calculate the 2d and 3d magnitudes of a given S|T combo, such as those found in the LRC's version of the LST's standard model of particle physics, and thereby hopefully match their observed magnetic and mass properties.
Re: Meeting a Terrific Challenge
Ok, the next step in our challenge is to relate the expansion of our 3d number system (i.e. √1, √2, √3), based on the radii of the the three balls defined by the LC, to our reciprocal numbers that constitute the S|T unit combos of the LRC's version of the standard model (sm).
In order to meet the terrific challenge of determining why the mass of the proton (~1836 MeV/c2) is so much more than the mass of the electron (~ .511 MeV/c2), we anticipate having to understand the 3d properties of the S|T combos.
However, it will also behoove us to understand the other two families of particles, the second and third families of quarks and leptons found in the LST's standard model of particle physics, especially their leptons, since the mass of these particles varies from that of the electron, but their charges do not.
The mass of the muon lepton is ~ 106 MeV/c2, and the mass of the tau lepton is ~ 1776.82 MeV/c2, and an investigation of these mass differences from the electron mass avoids the complication of multiple quarks with different masses in combination.
I don't know why taking this course in the development didn't occur to me before, except I guess it seemed too daunting to contemplate, so I just didn't, but, as it turns out, the solution might just follow as a consequence of the fundamental postulates, like all the rest! And why should we be surprised?
Now, the reason I think this might be so is I suspect the mysterious limit to three families of quarks and leptons has to do with the limit of the universe to three dimensions, and if that is the case, then the question becomes one of how this connection is realized. The only way I've been able to connect them is through our 3d number system. That is to say, by changing the unit measure for each family to the radius of the corresponding ball of the LC.
On this basis, the unit of the first family would be the √1, that of the second family √2, and that of the third √3. The unit of the first family has worked out very well, as I have shown now for years, but only in terms of integers not square roots. Yet, we can express the RN's of our sm combos in terms of square roots by simply substituting the square root unit for that of the integer:
S|T = 1(√1)/2(√1) + 1(√1)/1(√1) + 2(√1)/1(√1) = 4(√1)|4(√1),
which gives us the neutrino of the first family (called the electron family), when it is multiplied by the three S|T units constituting a neutrino, or 3 x 4(√1)|4(√1) = 12(√1)|12(√1) num. From there, we can calculate the num value of each quark and lepton and their anti-particles, as shown below:
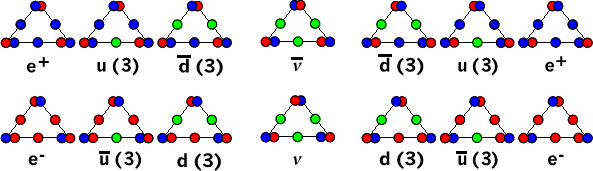
Where each balanced S|T unit (green) in a combo has a value of 4(√1)|4(√1) num, and each unbalanced S|T unit (red or blue) has a value of 6(√1)|6(√1) num. This works out to 14, 16 and 18 num in both "directions" from the neutrino's 12 num. Again, we have been amazed at how well these preon combos have worked out, in terms of 1d, or electrical properties, especially in terms of plus and minus beta decay, and the formation of protons and neutrons and the elements of the periodic table.
Yet, we have not been able to find the 2d (magnetic) or the 3d (mass) properties of these combinations, using the 1d RN, so the idea of identifying the three families with RNs employing the three different radii of the LC might be a good approach.
Since 12 is the square root of 144, we can use this value for the num of the electron neutrino, and this gives us √324|√324 (or 182) num for the electron & positron.
Accordingly, the neutrino of the second family's RN would be based on the √2 unit, giving it a value of 12(√2)|12(√2), or √288|√288 num. Thus, for the second family (called the muon family), the three green S|T units, constituting its neutrino, would have a value of √288/3, or √32:
υμ = √32 + √32 + √32 = √288
and unbalancing each subsequent combo by adding an additional 2d space or time unit to each of these in turn, gives us the sequence:
√72 + √32 + √32 = √392; √72 + √72 + √32 = √512; √72 + √72 + √72 = √648, or
-√648, -√512, -√392, √288, √392, √512, √648
Therefore, the 2d muons have a num of √648. Now, a μ- decays into a muon neutrino, √288 num, and a W- boson, so next we need the num of the 2d W- boson, which would be,
W- = 30(√2)|30(√2) num, or √1800|√1800 num,
given the 2d unit substitution in its calculation. Consequently, the difference between the num of the W bosons and the muons has to equal the num of the muon neutrinos:
√648 - √1800 = √288.
Like the 1d boson of beta decay, the 2d boson quickly decays into an electron and its anti-neutrino, but with a difference: Instead of a 1d electron and its 1d anti-neutrino, these would both have to be 2d combos, with 18(√2) num and 12(√2) num, respectively. I don't know what to make of that, yet.
As might be expected, the 3d case works out as well. The num of the neutrino of the third family (called the tau family), based on the 3d unit, √3, is 4(√3)|4(√3), or √432. Based on this value, the two tauons have a num of √972|√972 and the num of the 3d W bosons works out to √2700|√2700.
Hence the difference between the 3d tauons and the 3d bosons is √972 - √2700 = √432, which is the magnitude of the 3d tauon neutrino.
The decay of the tauons is almost identical to the decay of the muons, with the exception that the much heavier mass of the tauons allows their W bosons to decay into hadrons as well as leptons.
This must be yet another clue to the elusive 3d mass property of these combos. Hopefully, it'll help get us to the bottom of this mystery sooner than later.
In order to meet the terrific challenge of determining why the mass of the proton (~1836 MeV/c2) is so much more than the mass of the electron (~ .511 MeV/c2), we anticipate having to understand the 3d properties of the S|T combos.
However, it will also behoove us to understand the other two families of particles, the second and third families of quarks and leptons found in the LST's standard model of particle physics, especially their leptons, since the mass of these particles varies from that of the electron, but their charges do not.
The mass of the muon lepton is ~ 106 MeV/c2, and the mass of the tau lepton is ~ 1776.82 MeV/c2, and an investigation of these mass differences from the electron mass avoids the complication of multiple quarks with different masses in combination.
I don't know why taking this course in the development didn't occur to me before, except I guess it seemed too daunting to contemplate, so I just didn't, but, as it turns out, the solution might just follow as a consequence of the fundamental postulates, like all the rest! And why should we be surprised?
Now, the reason I think this might be so is I suspect the mysterious limit to three families of quarks and leptons has to do with the limit of the universe to three dimensions, and if that is the case, then the question becomes one of how this connection is realized. The only way I've been able to connect them is through our 3d number system. That is to say, by changing the unit measure for each family to the radius of the corresponding ball of the LC.
On this basis, the unit of the first family would be the √1, that of the second family √2, and that of the third √3. The unit of the first family has worked out very well, as I have shown now for years, but only in terms of integers not square roots. Yet, we can express the RN's of our sm combos in terms of square roots by simply substituting the square root unit for that of the integer:
S|T = 1(√1)/2(√1) + 1(√1)/1(√1) + 2(√1)/1(√1) = 4(√1)|4(√1),
which gives us the neutrino of the first family (called the electron family), when it is multiplied by the three S|T units constituting a neutrino, or 3 x 4(√1)|4(√1) = 12(√1)|12(√1) num. From there, we can calculate the num value of each quark and lepton and their anti-particles, as shown below:

Where each balanced S|T unit (green) in a combo has a value of 4(√1)|4(√1) num, and each unbalanced S|T unit (red or blue) has a value of 6(√1)|6(√1) num. This works out to 14, 16 and 18 num in both "directions" from the neutrino's 12 num. Again, we have been amazed at how well these preon combos have worked out, in terms of 1d, or electrical properties, especially in terms of plus and minus beta decay, and the formation of protons and neutrons and the elements of the periodic table.
Yet, we have not been able to find the 2d (magnetic) or the 3d (mass) properties of these combinations, using the 1d RN, so the idea of identifying the three families with RNs employing the three different radii of the LC might be a good approach.
Since 12 is the square root of 144, we can use this value for the num of the electron neutrino, and this gives us √324|√324 (or 182) num for the electron & positron.
Accordingly, the neutrino of the second family's RN would be based on the √2 unit, giving it a value of 12(√2)|12(√2), or √288|√288 num. Thus, for the second family (called the muon family), the three green S|T units, constituting its neutrino, would have a value of √288/3, or √32:
υμ = √32 + √32 + √32 = √288
and unbalancing each subsequent combo by adding an additional 2d space or time unit to each of these in turn, gives us the sequence:
√72 + √32 + √32 = √392; √72 + √72 + √32 = √512; √72 + √72 + √72 = √648, or
-√648, -√512, -√392, √288, √392, √512, √648
Therefore, the 2d muons have a num of √648. Now, a μ- decays into a muon neutrino, √288 num, and a W- boson, so next we need the num of the 2d W- boson, which would be,
W- = 30(√2)|30(√2) num, or √1800|√1800 num,
given the 2d unit substitution in its calculation. Consequently, the difference between the num of the W bosons and the muons has to equal the num of the muon neutrinos:
√648 - √1800 = √288.
Like the 1d boson of beta decay, the 2d boson quickly decays into an electron and its anti-neutrino, but with a difference: Instead of a 1d electron and its 1d anti-neutrino, these would both have to be 2d combos, with 18(√2) num and 12(√2) num, respectively. I don't know what to make of that, yet.
As might be expected, the 3d case works out as well. The num of the neutrino of the third family (called the tau family), based on the 3d unit, √3, is 4(√3)|4(√3), or √432. Based on this value, the two tauons have a num of √972|√972 and the num of the 3d W bosons works out to √2700|√2700.
Hence the difference between the 3d tauons and the 3d bosons is √972 - √2700 = √432, which is the magnitude of the 3d tauon neutrino.
The decay of the tauons is almost identical to the decay of the muons, with the exception that the much heavier mass of the tauons allows their W bosons to decay into hadrons as well as leptons.
This must be yet another clue to the elusive 3d mass property of these combos. Hopefully, it'll help get us to the bottom of this mystery sooner than later.
Re: Meeting a Terrific Challenge
It may seem bizarre at first glance, but the logic is sound I believe and the math is trivial, when we scale up the S|T combos of the LRC's version of the first family of the LST's standard model (sm) of particle physics, in order to calculate the combos of the second and third families, as described in the previous post above.
We did it by assuming that the three units of the LC are actually the basis for three valid number systems, and as such could each form a family of combos. The calculations work out for the two "new" families, because they work out for the first family, upon which they are based.
When I say "work out," I mean the balance of the 1d electrical charges work out for all three families, not the 2d magnetic and 3d mass calculations, because we don't know how to make those yet. However, in the previous post, I forgot to divide the W boson num values by the appropriate unit, which caused an error in the magnitudes of the decay products.
Recall, that the num of the W bosons in the beta decay process of the electron family is 30 or the square root of 900, while that of the W bosons of the muon family is the square root of 1800 and that of the tau family is the square root of 2700. However, when each of these latter num values are divided by their respective unit values, √2 and √3, they both come out to 30, which is the sum of the electron (18) and anti-neutrino (12), as they should be.
So, while I'm happy that we've been able to extend our new physics model like this, using the new math that has come out of the RST, I have to stress how tentative it is at this point, knowing that I may have made a foolish mistake again, as I have many times in the past.
With this said, however, I am happy to show how the theory fits nicely and naturally into the 3d numbers of the tetraktys table, which I recently shared in a previous post above. The three tables, one for each family, are shown below:
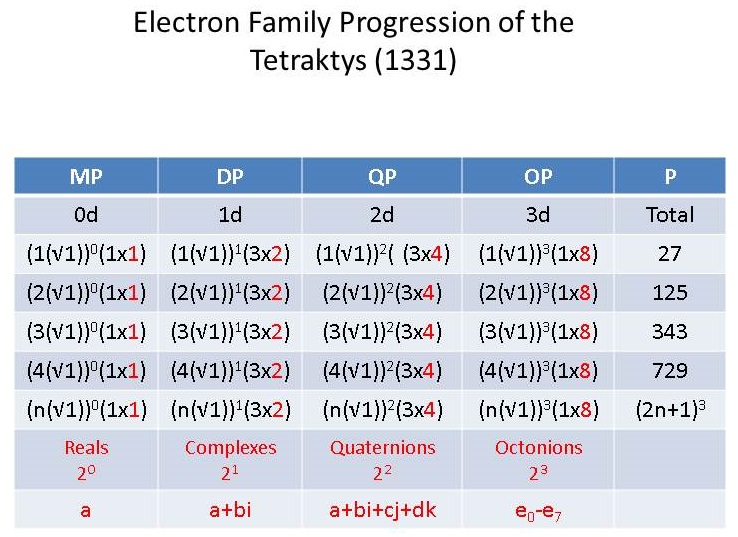
Table 1. Tetraktys (LC) Progression of First Family Magnitudes (Electron Family of Quarks and Leptons)
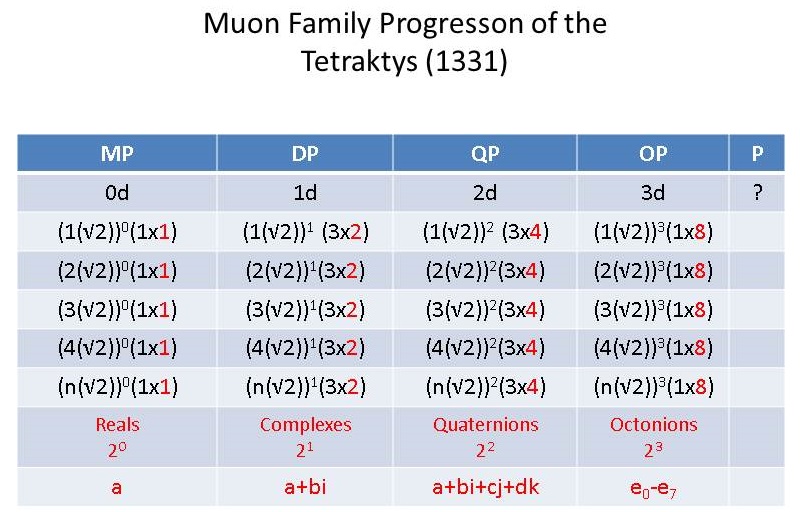
Table 2. Tetraktys (LC) Progression of Second Family Magnitudes (Muon Family of Quarks and Leptons)

Table 3. Tetraktys (LC) Progression of Third Family Magnitudes (Tau Family of Quarks and Leptons)
As can be seen from these tables, we only need to substitute the √2 and √3 for the normal unit of √1, in order to get the values of the next two families.
The progression of the 3d magnitudes of the electron family's tetraktys are then doubled for the muon family and tripled for the tau family:
1) Electron's 3d (LC) progression: 8, 64, 216, 512, ..., 2n3, n = 1, 2, 3, ..., ∞
2) Muon's 3d (LC) progression: 16, 128, 432, 1024, ..., 2(2n)3, n = 1, 2, 3, ..., ∞
3) Tau's 3d (LC) progression: 24, 192, 648, 1536, ..., 3(2n)3, n = 1, 2, 3, ..., ∞
I should mention that the corresponding LST multi-dimensional number systems shown in red at the bottom of the tables were placed in the original table for an unrelated reason and I just neglected to remove them.
The bottom line is that we now have three families of S|T combos that correspond to the three families of elementary particles found in the LST's standard model of particle physics. Recognizing that the LRC's model is strictly deduced from the RST's postulates, while the LST's model is constructed from empirical observations, and that the mathematics used to calculate the properties of the LRC's model stem from the intuition, or, in other words, are intuited, from those same postulates, or from nature, we might say, while the mathematics of the LST's model is based on questionable formalisms, or non-intuited axioms of doubtful origins (real, imaginary and theoretical numbers), we are very pleased, to say the least.
If only we can figure out how to calculate the 2d and 3d properties of all these particles!
We did it by assuming that the three units of the LC are actually the basis for three valid number systems, and as such could each form a family of combos. The calculations work out for the two "new" families, because they work out for the first family, upon which they are based.
When I say "work out," I mean the balance of the 1d electrical charges work out for all three families, not the 2d magnetic and 3d mass calculations, because we don't know how to make those yet. However, in the previous post, I forgot to divide the W boson num values by the appropriate unit, which caused an error in the magnitudes of the decay products.
Recall, that the num of the W bosons in the beta decay process of the electron family is 30 or the square root of 900, while that of the W bosons of the muon family is the square root of 1800 and that of the tau family is the square root of 2700. However, when each of these latter num values are divided by their respective unit values, √2 and √3, they both come out to 30, which is the sum of the electron (18) and anti-neutrino (12), as they should be.
So, while I'm happy that we've been able to extend our new physics model like this, using the new math that has come out of the RST, I have to stress how tentative it is at this point, knowing that I may have made a foolish mistake again, as I have many times in the past.
With this said, however, I am happy to show how the theory fits nicely and naturally into the 3d numbers of the tetraktys table, which I recently shared in a previous post above. The three tables, one for each family, are shown below:

Table 1. Tetraktys (LC) Progression of First Family Magnitudes (Electron Family of Quarks and Leptons)

Table 2. Tetraktys (LC) Progression of Second Family Magnitudes (Muon Family of Quarks and Leptons)

Table 3. Tetraktys (LC) Progression of Third Family Magnitudes (Tau Family of Quarks and Leptons)
As can be seen from these tables, we only need to substitute the √2 and √3 for the normal unit of √1, in order to get the values of the next two families.
The progression of the 3d magnitudes of the electron family's tetraktys are then doubled for the muon family and tripled for the tau family:
1) Electron's 3d (LC) progression: 8, 64, 216, 512, ..., 2n3, n = 1, 2, 3, ..., ∞
2) Muon's 3d (LC) progression: 16, 128, 432, 1024, ..., 2(2n)3, n = 1, 2, 3, ..., ∞
3) Tau's 3d (LC) progression: 24, 192, 648, 1536, ..., 3(2n)3, n = 1, 2, 3, ..., ∞
I should mention that the corresponding LST multi-dimensional number systems shown in red at the bottom of the tables were placed in the original table for an unrelated reason and I just neglected to remove them.
The bottom line is that we now have three families of S|T combos that correspond to the three families of elementary particles found in the LST's standard model of particle physics. Recognizing that the LRC's model is strictly deduced from the RST's postulates, while the LST's model is constructed from empirical observations, and that the mathematics used to calculate the properties of the LRC's model stem from the intuition, or, in other words, are intuited, from those same postulates, or from nature, we might say, while the mathematics of the LST's model is based on questionable formalisms, or non-intuited axioms of doubtful origins (real, imaginary and theoretical numbers), we are very pleased, to say the least.
If only we can figure out how to calculate the 2d and 3d properties of all these particles!
Re: Meeting a Terrific Challenge
Accepting a universe of motion is not easy for us, because we naturally see space and time as a stage for the interaction of pre-existing objects. And even after we reach an age where we can intellectually entertain the idea of nothing but motion, it's still difficult, because we are not equipped with a mathematical understanding that would facilitate the mental conception of such a thing.
Our algebra is based on pre-existing objects, just as our physics is based on it. From 1+1 = 2 and 1-1 = 0 and 1x1 = 1 and 1/1 = 1, we are taught to deal with numbers as objects that occupy one position at any one moment of time, just as the physical objects around us do. Objects can only move in one "direction" of one dimension at a time. To move in the two "directions" of a given dimension, an object must stop its motion in one "direction" and commence to move again in the opposite "direction," of that given dimension.
It is the same with our algebra. We measure magnitudes of space from one end to the other, in one "direction" in a given dimension, at a time. Length a is given a magnitude of measurement, then length b is given one in another dimension. If they are equal measures, their sum is double their measure, and their difference is zero; their product is the square of their measure, and their quotient is equal to their measure, and it goes on from there, if they are not equal.
However, we do not measure scalar motion magnitudes in the same way, because they are not based on the motion of pre-existent objects. These magnitudes are constantly progressing and to measure them, we have to pick a point in time of that progression and a subsequent point in time in reference to it. Thus, it is an algebra of "order in progression," rather than the usual algebra based on "magnitude of substance," to borrow Hamilton's terminology (see here).
These order in progression magnitudes can oscillate, however, just as objects do, but the result is quite different, because the motion of change of scale is simultaneous in both "directions." The movement of scalar oscillation alternately expands and contracts, instead of vibrating back and forth, as the oscillating movement of an object does.
Therefore, the corresponding time-based algebra used to describe the scalar oscillation must be different than the substance-based algebra, used to describe the vibration. Using the substance algebra to describe a vibrating object, such as a back and forth swinging pendulum, for instance, the algebra calculates a changing position over time, whereas the time algebra calculates a changing size over time. These are two different concepts to be sure.
In another example, the hypotenuse of a right triangle is the square root of the sum of the squares of its sides, an irrational number, in substance algebra, but in time algebra, one side of the triangle is considered the reciprocal of the other, because they are orthogonal, so the hypotenuse is effectively transformed into a radius of a circle segment, which is the quotient of the two, orthogonal numbers, i.e. a/b = c, or r = a = b = c.
This then leads to another fundamental difference between the two algebras. In the case of scalar oscillation, r is cut in half, or doubled, depending upon the difference or "displacement" between them. In substance algebra, given integer displacements (i.e. n = 1, 2, 3, ...∞), side c is the same irrational number regardless whether or not side a > side b, or vice versa.
With the time algebra it's quite different. If side a > side b, then r expands, but if side b > a, r contracts. This difference is huge because it is tantamount to the difference between the integer number line, with datum 0, and the rational number line, with datum 1. Both are legitimate, but the integer line is a derivative of the more fundamental rational line.
The rational line has two "directions," while the integer line really has only one "direction." It is made to have two "directions" via the expediency of adding polarity signs to the integers to differentiate between two "directions." It doesn't come by this polarity naturally, though, so it requires another expediency, called the imaginary number, "i," further complicating our understanding, if the difference between the two algebras is not recognized.
In the new scalar mathematics that the LRC calls the reciprocal system of mathematics, both algebras are used, where the integer number line, with datum -1+1=0, is a measure of displacement from unit measure (1/1), and the rational number line, with datum 1/1=1, is a measure of oscillation. A unit of oscillation has a unit of displacement, in one of two "directions." It is an oscillation measure of less than unity or an oscillation measure of greater than unity. These are the only possibilities.
The algebra of the oscillations is synonymous with a third algebra consisting of a union between the substance algebra and the time algebra, where 1/2 + 2/1 = 0, in one sense ((-1) + (+1)), but 3/3 (or 1/1) in another sense, depending upon one's point of view. The sum of the latter (3/3) is misleading, however, because the two oscillations have to be summed over the unit boundary: 1/2 +1/1+2/1 = 4/4; That is to say, the oscillations cannot exist independent of the unit expansion, otherwise there is no unit motion to oscillate, by creating a unit displacement in the two "directions."
The bottom line is this: We cannot consistently revise our concept of a universe of matter to a concept of a universe of scalar motion, without revising our concept of numbers and their algebra, which we use to combine them and quantify the relations between them.
Our algebra is based on pre-existing objects, just as our physics is based on it. From 1+1 = 2 and 1-1 = 0 and 1x1 = 1 and 1/1 = 1, we are taught to deal with numbers as objects that occupy one position at any one moment of time, just as the physical objects around us do. Objects can only move in one "direction" of one dimension at a time. To move in the two "directions" of a given dimension, an object must stop its motion in one "direction" and commence to move again in the opposite "direction," of that given dimension.
It is the same with our algebra. We measure magnitudes of space from one end to the other, in one "direction" in a given dimension, at a time. Length a is given a magnitude of measurement, then length b is given one in another dimension. If they are equal measures, their sum is double their measure, and their difference is zero; their product is the square of their measure, and their quotient is equal to their measure, and it goes on from there, if they are not equal.
However, we do not measure scalar motion magnitudes in the same way, because they are not based on the motion of pre-existent objects. These magnitudes are constantly progressing and to measure them, we have to pick a point in time of that progression and a subsequent point in time in reference to it. Thus, it is an algebra of "order in progression," rather than the usual algebra based on "magnitude of substance," to borrow Hamilton's terminology (see here).
These order in progression magnitudes can oscillate, however, just as objects do, but the result is quite different, because the motion of change of scale is simultaneous in both "directions." The movement of scalar oscillation alternately expands and contracts, instead of vibrating back and forth, as the oscillating movement of an object does.
Therefore, the corresponding time-based algebra used to describe the scalar oscillation must be different than the substance-based algebra, used to describe the vibration. Using the substance algebra to describe a vibrating object, such as a back and forth swinging pendulum, for instance, the algebra calculates a changing position over time, whereas the time algebra calculates a changing size over time. These are two different concepts to be sure.
In another example, the hypotenuse of a right triangle is the square root of the sum of the squares of its sides, an irrational number, in substance algebra, but in time algebra, one side of the triangle is considered the reciprocal of the other, because they are orthogonal, so the hypotenuse is effectively transformed into a radius of a circle segment, which is the quotient of the two, orthogonal numbers, i.e. a/b = c, or r = a = b = c.
This then leads to another fundamental difference between the two algebras. In the case of scalar oscillation, r is cut in half, or doubled, depending upon the difference or "displacement" between them. In substance algebra, given integer displacements (i.e. n = 1, 2, 3, ...∞), side c is the same irrational number regardless whether or not side a > side b, or vice versa.
With the time algebra it's quite different. If side a > side b, then r expands, but if side b > a, r contracts. This difference is huge because it is tantamount to the difference between the integer number line, with datum 0, and the rational number line, with datum 1. Both are legitimate, but the integer line is a derivative of the more fundamental rational line.
The rational line has two "directions," while the integer line really has only one "direction." It is made to have two "directions" via the expediency of adding polarity signs to the integers to differentiate between two "directions." It doesn't come by this polarity naturally, though, so it requires another expediency, called the imaginary number, "i," further complicating our understanding, if the difference between the two algebras is not recognized.
In the new scalar mathematics that the LRC calls the reciprocal system of mathematics, both algebras are used, where the integer number line, with datum -1+1=0, is a measure of displacement from unit measure (1/1), and the rational number line, with datum 1/1=1, is a measure of oscillation. A unit of oscillation has a unit of displacement, in one of two "directions." It is an oscillation measure of less than unity or an oscillation measure of greater than unity. These are the only possibilities.
The algebra of the oscillations is synonymous with a third algebra consisting of a union between the substance algebra and the time algebra, where 1/2 + 2/1 = 0, in one sense ((-1) + (+1)), but 3/3 (or 1/1) in another sense, depending upon one's point of view. The sum of the latter (3/3) is misleading, however, because the two oscillations have to be summed over the unit boundary: 1/2 +1/1+2/1 = 4/4; That is to say, the oscillations cannot exist independent of the unit expansion, otherwise there is no unit motion to oscillate, by creating a unit displacement in the two "directions."
The bottom line is this: We cannot consistently revise our concept of a universe of matter to a concept of a universe of scalar motion, without revising our concept of numbers and their algebra, which we use to combine them and quantify the relations between them.
Re: Meeting a Terrific Challenge
The assertion that new bottles are needed for new wine is very old and wise, and evidently it's true in our case as well. We portend to offer a new and powerful paradigm for viewing the universe, but without a new bottle to put it in, the new wine tends to leak away. Could it be true that we have found a new bottle in what we are calling the reciprocal system of mathematics?
In our new system of physical theory, we have found that the integer number system, with datum (-1)+(+1) = 0, can be misleading, and the rational number system, with datum 1/1 = 1 actually generates the integer system and is therefore more fundamental, when the integer numbers are viewed as displacements from rational unity, either in the numerator or the denominator.
We also find that, while our new system postulates discrete units only, irrational numbers are found in the geometry and the mathematics of the three dimensional scalar motion that our new system also posits. These are the square roots of 1, 2 and 3. What we at the LRC are now contending, is that these three square roots can each serve as the basis for three different, but related number systems.
Whether or not this assertion is justified, only time will tell, but in the meantime, we notice that the three families of quarks and leptons found in the LST's standard model of particle physics can be generated from these three number systems, at least in the one-dimensional case, where electrical charges account for their properties.
Yet, that work is very preliminary and subject to change as our understanding of these proposed number systems grows. As those who have been following these posts know, the basis for our scalar algebra is found in the numbers of the tetraktys and the geometry of Larson's cube (LC), the 3d stack of 8 one-unit cubes that is generated by the progression of the multi-dimensional tetraktys. The algebra calculates the progression of the stack and the stack's geometry determines the progression of the three radii, which are the square roots of 1, 2 and 3.
Now, in the LRC's RST-based theory (our RSt, if you will), if the progression of the stack begins to oscillate at some point, it creates oscillating entities of space over time and also their reciprocal units, oscillating entities of time over space, and these are combined to form a ratio of space/time oscillations to time/space oscillations, which simply count the quantity of space versus time oscillations in combination.
Of course, these quantities may be equal, or unequal, and, if they are unequal, one may be greater or lesser than the other, which forms an "order in progression" algebra, upon which we can build an algebraic science, that can contain ("bottle?") the well-established science of geometry, used in our new scalar system, thereby satisfying what we may characterize as "Hamilton's complaint."
As already mentioned previously, the three square roots can be shown to be valid multi-dimensional units of numbers in at least two ways. The first way is by examining the three balls defined by the 3d stacks. The radius of the inner ball, contained by the stack, is the square root of 1, while the radius of the ball that just contains a 2d slice of the stack is the square root of 2, and the radius of the ball just containing the stack is the square root of 3. Rotating these three radii down to the horizontal line, pointing to the right from the origin, it can be seen how they form three units on a number line. This is a geometric representation.
The second way to see the same thing is doing so algebraically, using the Pythagorean theorem, where each of the three dimensional units are used in the calculation, as follows:
1) √((√1)2+(√1)2+(√1)2) = √(1+1+1) = √3;
2) √((√1)2+(√1)2+(√0)2) = √(1+1+0) = √2;
3) √((√1)2+(√0)2+(√0)2) = √(1+0+0) = √1;
But then using each of these units as units of measure in the expansion, we get two more sets:
1) √((√2)2+(√2)2+(√2)2) = √(2+2+2) = √6;
2) √((√2)2+(√2)2+(√0)2) = √(2+2+0) = √4;
3) √((√2)2+(√0)2+(√0)2) = √(2+0+0) = √2;
and
1) √((√3)2+(√3)2+(√3)2) = √(3+3+3) = √9;
2) √((√3)2+(√3)2+(√0)2) = √(3+3+0) = √6;
3) √((√3)2+(√0)2+(√0)2) = √(3+0+0) = √3;
So, from these calculations, we see at least two very interesting items. First, we see that the 1d value in each case is one of our square roots, but only in the first set, the 1d set we might say, is the square root an integer, i.e. √1 = 1. Second, however, we see that the 2d value in the 2d set is an integer (√4 = 2), and the 3d value in the 3d set is also an integer (√9 = 3).
It's no coincidence that I chose these three colors to highlight the dimensional integers, because I suspect that they play into the so-called "color" charges of the LST's quark combos constituting the protons and neutrons.
We'll see. Stay tuned.
In our new system of physical theory, we have found that the integer number system, with datum (-1)+(+1) = 0, can be misleading, and the rational number system, with datum 1/1 = 1 actually generates the integer system and is therefore more fundamental, when the integer numbers are viewed as displacements from rational unity, either in the numerator or the denominator.
We also find that, while our new system postulates discrete units only, irrational numbers are found in the geometry and the mathematics of the three dimensional scalar motion that our new system also posits. These are the square roots of 1, 2 and 3. What we at the LRC are now contending, is that these three square roots can each serve as the basis for three different, but related number systems.
Whether or not this assertion is justified, only time will tell, but in the meantime, we notice that the three families of quarks and leptons found in the LST's standard model of particle physics can be generated from these three number systems, at least in the one-dimensional case, where electrical charges account for their properties.
Yet, that work is very preliminary and subject to change as our understanding of these proposed number systems grows. As those who have been following these posts know, the basis for our scalar algebra is found in the numbers of the tetraktys and the geometry of Larson's cube (LC), the 3d stack of 8 one-unit cubes that is generated by the progression of the multi-dimensional tetraktys. The algebra calculates the progression of the stack and the stack's geometry determines the progression of the three radii, which are the square roots of 1, 2 and 3.
Now, in the LRC's RST-based theory (our RSt, if you will), if the progression of the stack begins to oscillate at some point, it creates oscillating entities of space over time and also their reciprocal units, oscillating entities of time over space, and these are combined to form a ratio of space/time oscillations to time/space oscillations, which simply count the quantity of space versus time oscillations in combination.
Of course, these quantities may be equal, or unequal, and, if they are unequal, one may be greater or lesser than the other, which forms an "order in progression" algebra, upon which we can build an algebraic science, that can contain ("bottle?") the well-established science of geometry, used in our new scalar system, thereby satisfying what we may characterize as "Hamilton's complaint."
As already mentioned previously, the three square roots can be shown to be valid multi-dimensional units of numbers in at least two ways. The first way is by examining the three balls defined by the 3d stacks. The radius of the inner ball, contained by the stack, is the square root of 1, while the radius of the ball that just contains a 2d slice of the stack is the square root of 2, and the radius of the ball just containing the stack is the square root of 3. Rotating these three radii down to the horizontal line, pointing to the right from the origin, it can be seen how they form three units on a number line. This is a geometric representation.
The second way to see the same thing is doing so algebraically, using the Pythagorean theorem, where each of the three dimensional units are used in the calculation, as follows:
1) √((√1)2+(√1)2+(√1)2) = √(1+1+1) = √3;
2) √((√1)2+(√1)2+(√0)2) = √(1+1+0) = √2;
3) √((√1)2+(√0)2+(√0)2) = √(1+0+0) = √1;
But then using each of these units as units of measure in the expansion, we get two more sets:
1) √((√2)2+(√2)2+(√2)2) = √(2+2+2) = √6;
2) √((√2)2+(√2)2+(√0)2) = √(2+2+0) = √4;
3) √((√2)2+(√0)2+(√0)2) = √(2+0+0) = √2;
and
1) √((√3)2+(√3)2+(√3)2) = √(3+3+3) = √9;
2) √((√3)2+(√3)2+(√0)2) = √(3+3+0) = √6;
3) √((√3)2+(√0)2+(√0)2) = √(3+0+0) = √3;
So, from these calculations, we see at least two very interesting items. First, we see that the 1d value in each case is one of our square roots, but only in the first set, the 1d set we might say, is the square root an integer, i.e. √1 = 1. Second, however, we see that the 2d value in the 2d set is an integer (√4 = 2), and the 3d value in the 3d set is also an integer (√9 = 3).
It's no coincidence that I chose these three colors to highlight the dimensional integers, because I suspect that they play into the so-called "color" charges of the LST's quark combos constituting the protons and neutrons.
We'll see. Stay tuned.
Re: Meeting a Terrific Challenge
Sometimes it's hard to fight the doubts that what we have developed and are still developing is something significant and worthwhile. This is especially true when I read the CERN propaganda heralding the accomplishments of the LST, such as the so-called completion of the standard model of particle physics with the "discovery" of the Higgs boson, requiring the LST community to accept the notion of the Higgs field, permeating all space and giving mass to some particles, but not others (see here.)
They blissfully bask in the light of their work, inviting all to join in the celebration with them, while ignoring the glare of the inherent contradictions they know full-well are there. True, Stephen Hawking lost his bet that they wouldn't find the Higgs, but the fact that they claimed to have found it doesn't change his characterization of the standard model theory as "ugly and ad hoc" (see here.)
They still talk of finding supersymmetry to save string theory, as if that's possible, and at the same time hail the report of the detection of gravity waves, without even offering a hint as to the disastrous incompatibility of the two theories underlying the quantum and continuum experiments.
And then, if that isn't bad enough, Hestenes' geometric algebra (GA), which we briefly entertained as a basis for RST mathematics many years ago, when it was still rather esoteric, is now so wide-spread that there are countless YouTube videos explaining it glibly! (For instance, see here) Not that there's anything wrong with that in our world of vector motion, but its success reinforces the philosophical hold that the LST has on the unsuspecting public that there's not more to be said.
Scalar motion, the observed motion of the expanding universe and the inverse of it, the gravitational motion of matter, is not even acknowledged as a worthy consideration for investigation, as the continual fight for the acceptance of a Wikipedia article on Larson and his work, attests.
When we looked at GA, with its connection to Clifford algebras, it was exciting to learn that scalars, vectors, bivectors and trivectors followed from the binomial expansion of the tetraktys (or Pascal's triangle). At least GA was a clarification of the confusion emerging from the view of the four, normed division algebras, the reals, complexes, quaternions and octonians, where the four dimensions, 0, 1, 2, 3, are confused with the number of their respective "directions," 1, 2, 4 and 8.
Of course, what we didn't realize at the time was that, although GA maintains the properties of algebra, unlike the four division algebras, which lose two of those three properties, as the "dimension" of the algebra increases, it may have lost the all-important property of triality, just as those algebras do.
Although I may stand corrected on the point of the triality of GA, one thing I know for sure is that its application of vectors to the binomial expansion of the tetraktys will not work for an RST algebra, because scalar motion, like scalar numbers, are quantities of magnitude only. It's true that they have "direction" (e.g. larger, smaller; expansion, contraction; in, out; etc.), but they don't have the infinite number of directions that vectors do, which gives rise to GA's extra property of "orientation."
It's great that the geometric product of GA enables the algebraic manipulation of vector spaces by increasing or decreasing the dimensions of the spaces, since that is so useful in LST work, but it hinders us in our efforts to raise the public's awareness that, at the fundamental level, there is an entirely different type of motion that needs to be understood, and it can be easily understood, when one considers that the dimensions of time and space in the tetraktys (0, 1, 2, 3, respectively) can be understood in terms of the duality of their scalar "directions" (1, 2, 4, 8, or powers of 2, respectively), as well as the "blades" of GA.
The Greeks thought of the tetraktys in terms of the monad (1), dyad (2), triad (3) and tetrad (4), emerging as the complexity of the universe unfolds, and that's not far off, but modern math has lost sight of this universal truth and how to interpret it.
Now, GA comes much closer to the truth; However, because Hestenes knows nothing regarding scalar motion (we approached him with the idea, but he thought we were crazy,) the scalar "directions" of the four dimensions are misinterpreted, as directions of basis vectors, not as multi-dimensional scalar spaces, generated by scalar motion.
Recall how we can quantify Pascal's triangle, in terms of the number of poles it generates in each dimension, which turns out to be powers of 3, because, as the ancient Greeks understood it, poles (i.e. opposites) are not possible without a middle; everything has to have a middle, or center, including numbers:
0d------- 1(20) = 30 = 1 pole
1d-------1(20)+1(21) = 31 = 3 poles
2d------1(20)+2(21)+1(22) = 32 = 9 poles
3d-----1(20)+3(21)+3(22)+1(23) = 33 = 27 poles.
The Greek idea was that "Things that had a beginning, middle and end, [should be] denoted by the number Three, saying that anything that has a middle is triform, which was applied to every perfect thing." (see Quote from Porphyryhere)
Of course, a scalar change of anything is, by definition, an increase (decrease) in the two "directions" of each dimension of that object or figure, or number, which dictates an unchanging middle, or center, from which all such change is referenced.
Hence, the number of poles in each level of the triangle (i.e. dimension) always includes the scalar, or point, from which the rest are measured, so the numbers of Pascal's triangle, 1, 11, 121, 1331, are summed left to right, starting with the ever present scalar on the left for each dimension, and giving us the total number of "directions" as the dimensions increase from 0 to 3:
0d: 1
1d: 1+1 = 2
2d: 1+2+1 = 4
3d: 1+3+3+1 = 8
but the number of poles in each dimension increases as a power of 3, because each succeeding dimension appends the number of its "directions" in that dimension to the number of "directions" of the preceding dimensions:
0d: 1(20) = 30 = 1
1d: 1(20)+1(21) = 31 = 3
2d: 1(20)+2(21)+1(22) = 32 = 9
3d: 1(20)+3(21)+3(22)+1(23) = 33 = 27
Consequently, there is a lot of information in the numbers of Pascal's triangle, and the fact that they relate directly to the geometry of Larson's cube is deep and profound, as regards the nature of the numbers of the progressive algebra and the magnitudes of geometry. The following graphic is an attempt to capture some of it:
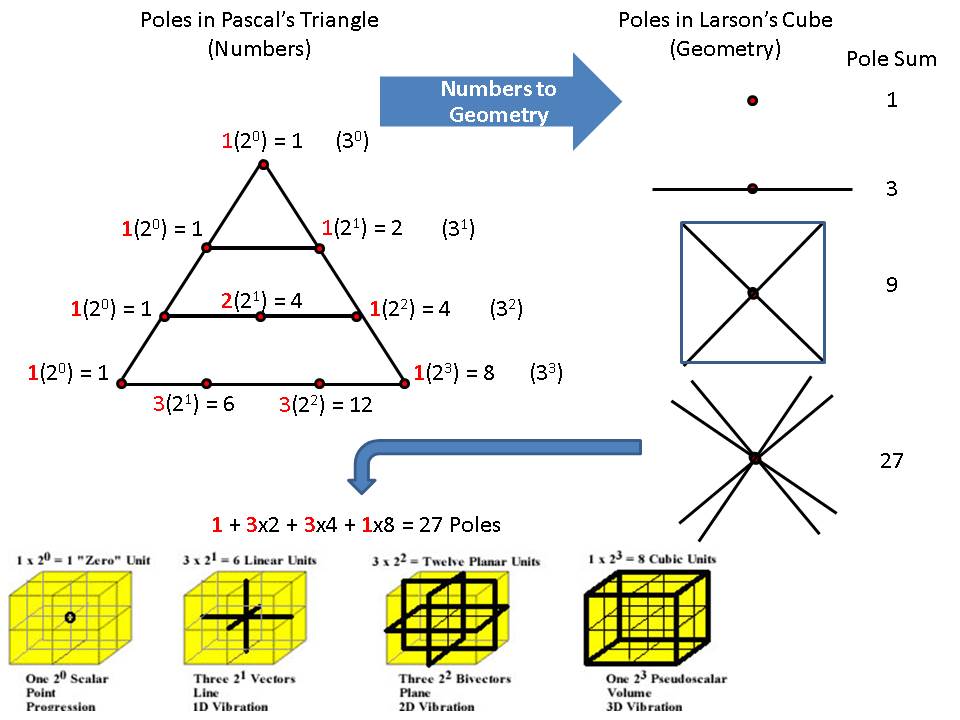
Given the discovery of this close one-to-one correspondence of numbers to geometry, the motivation to understand a corresponding multi-dimensional algebra of the numbers is very high, and we have been working on it, but, in the meantime, GA applies the dimensional, directional and polarizational properties of the numerical and geometrical transformation depicted in the graphic above to the vector motion of the LST:
The basis elements of GA multivectors correspond to the numbers of Pascal's triangle:
0d: 1 ----------------grade 0------scalar (1);
1d: 11 ---------------grade 1------scalar and vector (2);
2d: 121 -------------grade 2------scalar, 2 vectors and a bivector (4);
3d: 1331 ------------grade 3------scalar, 3 vectors, 3 bivectors and a trivector (8).
Using GA, with these multivectors and combinations of them, Hestenes is able to reduce the four Maxwell equations of electromagnetism in vector space to one equation and solve some long-standing issues of quantum mechanics. Defining GA with these elements and their algebraic rules of operations, Hestenes declares: "[GA] as the leading candidate to unify mathematics in the 21st century." (See page 146 of published interview here.)
In contemplating the situation, though, those few of us who have adopted Larson's view of a universe of motion see the vector motion of the LST as a subset of the scalar motion of the RST, valid in it's own realm, but without the underlying knowledge of scalar motion, it lacks conceptual clarity.
Units of space, or units of time, whether in the form of a 0d point, 1d line, 2d area or 3d volume, are related in a very fundamental way that must be clearly understood if one is to avoid confusion, because there are at least three ways to form them:
1) Change of position, or unidirectional motion (motion in 6 "directions," choose 1;
2) Change of interval, or bidirectional motion (motion in 6 "directions" choose 2;
3) Change of scale, or tridirectional motion (motion in 8 "directions.")
Clearly, all the units of space and time can be built up algebraically from the vector type motion (change of position motion) and it's a good thing, but not always the best choice, if we don't want to over complicate things. A 3d change of scale, with its 1d and 2d components, is manifestly easier to understand than constructing these components via combinations of GA scalars, vectors, bivectors, and trivectors, utilizing the geometric product.
But it's not just a matter of simpler is better. It should be understood that, in a given context, it's totally inadequate and inappropriate. I suppose you could construct the initial 3d scalar number, the 2x2x2 stack of 8, 1-unit cubes, with GA's multivectors, but not only would it be very tedious to do so, it would not lead to the subsequent quantities of 64, 216, 512, etc in any well-motivated manner.
The truth is, the GA trivector is simply a 1x1x1 cube (or ball with radius 1), and rotating it over time completes a 360 degrees cycle, not a 720 degree cycle, per unit of time, which quantum theory must have. I know they can make it work for quantum spin anyway, but not in the straight-forward way that the 3d scalar expansion/contraction does.
If they could, then they would undoubtedly find the essential property of triality in GA and this would enable them to build the entities of the standard model as we have done. But it can't be done with complex numbers, because they lose the property of triality, by going to the unit circle, and I suspect it can't be done with GA either, but I maybe wrong.
Perhaps a reader in this forum knows and can explain it? If so, please feel free to do so, okay?
They blissfully bask in the light of their work, inviting all to join in the celebration with them, while ignoring the glare of the inherent contradictions they know full-well are there. True, Stephen Hawking lost his bet that they wouldn't find the Higgs, but the fact that they claimed to have found it doesn't change his characterization of the standard model theory as "ugly and ad hoc" (see here.)
They still talk of finding supersymmetry to save string theory, as if that's possible, and at the same time hail the report of the detection of gravity waves, without even offering a hint as to the disastrous incompatibility of the two theories underlying the quantum and continuum experiments.
And then, if that isn't bad enough, Hestenes' geometric algebra (GA), which we briefly entertained as a basis for RST mathematics many years ago, when it was still rather esoteric, is now so wide-spread that there are countless YouTube videos explaining it glibly! (For instance, see here) Not that there's anything wrong with that in our world of vector motion, but its success reinforces the philosophical hold that the LST has on the unsuspecting public that there's not more to be said.
Scalar motion, the observed motion of the expanding universe and the inverse of it, the gravitational motion of matter, is not even acknowledged as a worthy consideration for investigation, as the continual fight for the acceptance of a Wikipedia article on Larson and his work, attests.
When we looked at GA, with its connection to Clifford algebras, it was exciting to learn that scalars, vectors, bivectors and trivectors followed from the binomial expansion of the tetraktys (or Pascal's triangle). At least GA was a clarification of the confusion emerging from the view of the four, normed division algebras, the reals, complexes, quaternions and octonians, where the four dimensions, 0, 1, 2, 3, are confused with the number of their respective "directions," 1, 2, 4 and 8.
Of course, what we didn't realize at the time was that, although GA maintains the properties of algebra, unlike the four division algebras, which lose two of those three properties, as the "dimension" of the algebra increases, it may have lost the all-important property of triality, just as those algebras do.
Although I may stand corrected on the point of the triality of GA, one thing I know for sure is that its application of vectors to the binomial expansion of the tetraktys will not work for an RST algebra, because scalar motion, like scalar numbers, are quantities of magnitude only. It's true that they have "direction" (e.g. larger, smaller; expansion, contraction; in, out; etc.), but they don't have the infinite number of directions that vectors do, which gives rise to GA's extra property of "orientation."
It's great that the geometric product of GA enables the algebraic manipulation of vector spaces by increasing or decreasing the dimensions of the spaces, since that is so useful in LST work, but it hinders us in our efforts to raise the public's awareness that, at the fundamental level, there is an entirely different type of motion that needs to be understood, and it can be easily understood, when one considers that the dimensions of time and space in the tetraktys (0, 1, 2, 3, respectively) can be understood in terms of the duality of their scalar "directions" (1, 2, 4, 8, or powers of 2, respectively), as well as the "blades" of GA.
The Greeks thought of the tetraktys in terms of the monad (1), dyad (2), triad (3) and tetrad (4), emerging as the complexity of the universe unfolds, and that's not far off, but modern math has lost sight of this universal truth and how to interpret it.
Now, GA comes much closer to the truth; However, because Hestenes knows nothing regarding scalar motion (we approached him with the idea, but he thought we were crazy,) the scalar "directions" of the four dimensions are misinterpreted, as directions of basis vectors, not as multi-dimensional scalar spaces, generated by scalar motion.
Recall how we can quantify Pascal's triangle, in terms of the number of poles it generates in each dimension, which turns out to be powers of 3, because, as the ancient Greeks understood it, poles (i.e. opposites) are not possible without a middle; everything has to have a middle, or center, including numbers:
0d------- 1(20) = 30 = 1 pole
1d-------1(20)+1(21) = 31 = 3 poles
2d------1(20)+2(21)+1(22) = 32 = 9 poles
3d-----1(20)+3(21)+3(22)+1(23) = 33 = 27 poles.
The Greek idea was that "Things that had a beginning, middle and end, [should be] denoted by the number Three, saying that anything that has a middle is triform, which was applied to every perfect thing." (see Quote from Porphyryhere)
Of course, a scalar change of anything is, by definition, an increase (decrease) in the two "directions" of each dimension of that object or figure, or number, which dictates an unchanging middle, or center, from which all such change is referenced.
Hence, the number of poles in each level of the triangle (i.e. dimension) always includes the scalar, or point, from which the rest are measured, so the numbers of Pascal's triangle, 1, 11, 121, 1331, are summed left to right, starting with the ever present scalar on the left for each dimension, and giving us the total number of "directions" as the dimensions increase from 0 to 3:
0d: 1
1d: 1+1 = 2
2d: 1+2+1 = 4
3d: 1+3+3+1 = 8
but the number of poles in each dimension increases as a power of 3, because each succeeding dimension appends the number of its "directions" in that dimension to the number of "directions" of the preceding dimensions:
0d: 1(20) = 30 = 1
1d: 1(20)+1(21) = 31 = 3
2d: 1(20)+2(21)+1(22) = 32 = 9
3d: 1(20)+3(21)+3(22)+1(23) = 33 = 27
Consequently, there is a lot of information in the numbers of Pascal's triangle, and the fact that they relate directly to the geometry of Larson's cube is deep and profound, as regards the nature of the numbers of the progressive algebra and the magnitudes of geometry. The following graphic is an attempt to capture some of it:

Given the discovery of this close one-to-one correspondence of numbers to geometry, the motivation to understand a corresponding multi-dimensional algebra of the numbers is very high, and we have been working on it, but, in the meantime, GA applies the dimensional, directional and polarizational properties of the numerical and geometrical transformation depicted in the graphic above to the vector motion of the LST:
The basis elements of GA multivectors correspond to the numbers of Pascal's triangle:
0d: 1 ----------------grade 0------scalar (1);
1d: 11 ---------------grade 1------scalar and vector (2);
2d: 121 -------------grade 2------scalar, 2 vectors and a bivector (4);
3d: 1331 ------------grade 3------scalar, 3 vectors, 3 bivectors and a trivector (8).
Using GA, with these multivectors and combinations of them, Hestenes is able to reduce the four Maxwell equations of electromagnetism in vector space to one equation and solve some long-standing issues of quantum mechanics. Defining GA with these elements and their algebraic rules of operations, Hestenes declares: "[GA] as the leading candidate to unify mathematics in the 21st century." (See page 146 of published interview here.)
In contemplating the situation, though, those few of us who have adopted Larson's view of a universe of motion see the vector motion of the LST as a subset of the scalar motion of the RST, valid in it's own realm, but without the underlying knowledge of scalar motion, it lacks conceptual clarity.
Units of space, or units of time, whether in the form of a 0d point, 1d line, 2d area or 3d volume, are related in a very fundamental way that must be clearly understood if one is to avoid confusion, because there are at least three ways to form them:
1) Change of position, or unidirectional motion (motion in 6 "directions," choose 1;
2) Change of interval, or bidirectional motion (motion in 6 "directions" choose 2;
3) Change of scale, or tridirectional motion (motion in 8 "directions.")
Clearly, all the units of space and time can be built up algebraically from the vector type motion (change of position motion) and it's a good thing, but not always the best choice, if we don't want to over complicate things. A 3d change of scale, with its 1d and 2d components, is manifestly easier to understand than constructing these components via combinations of GA scalars, vectors, bivectors, and trivectors, utilizing the geometric product.
But it's not just a matter of simpler is better. It should be understood that, in a given context, it's totally inadequate and inappropriate. I suppose you could construct the initial 3d scalar number, the 2x2x2 stack of 8, 1-unit cubes, with GA's multivectors, but not only would it be very tedious to do so, it would not lead to the subsequent quantities of 64, 216, 512, etc in any well-motivated manner.
The truth is, the GA trivector is simply a 1x1x1 cube (or ball with radius 1), and rotating it over time completes a 360 degrees cycle, not a 720 degree cycle, per unit of time, which quantum theory must have. I know they can make it work for quantum spin anyway, but not in the straight-forward way that the 3d scalar expansion/contraction does.
If they could, then they would undoubtedly find the essential property of triality in GA and this would enable them to build the entities of the standard model as we have done. But it can't be done with complex numbers, because they lose the property of triality, by going to the unit circle, and I suspect it can't be done with GA either, but I maybe wrong.
Perhaps a reader in this forum knows and can explain it? If so, please feel free to do so, okay?
Re: Meeting a Terrific Challenge
I just happened upon a TED talk video by one James Beecham, a young man who is employed as a CERN physicist, working on what he calls a theoretical "disaster." Of course, he's referring to the "trouble with physics," which is the name of one of my blogs, which namesake is the title of Lee Smolin's anti-string theory book, published a few years ago.
The crux of the problem is the ancient one of squaring the circle. That is, the reconciling of the discrete-based quantum theory with the continuum-based general relativity theory, in order to unify the LST's physical theory - it can't be done and there's proof of that now, but they keep spending billions of dollars trying. What James tells his audience is that when they finally give up trying, it will not be the end of physics, but the beginning.
At that point they will need a fresh approach, one that Peter Woit contends will have to unify LST mathematics with its physics first. I've commented extensively about that over the years, but now that it's apparent that we can unite the algebra of time (or progression) with the algebra of space, to obtain a universal algebra of space/time (time/space), we can legitimately declare that the new beginning of physics has already commenced.
Of course, to convince the skeptics, we need to demonstrate the truth of our unification of numbers of the progression with the right lines and circles of geometry, which I think we can do with the tetraktys and Larson's cube (LC) and the world line chart.
We've already shown how the expansion of the tetraktys follows that of the LC, in 0, 1, 2 and 3 dimensions, since the two are mapped together, we might say. Recall how we identify the binary expansion of the tetraktys with the expansions of the two "directions" of each dimension in Pascal's triangle:
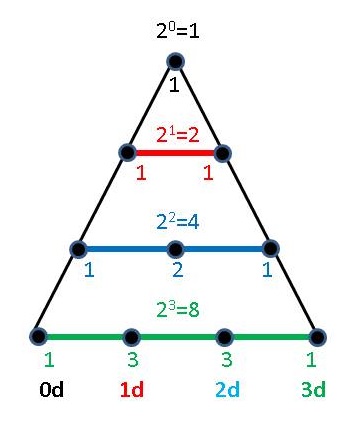
Figure 1. Binary Expansion of Four Dimensions of Tetraktys and Pascal's Triangle
In figure 1 above, the dimension 0 (black) has 20 = 1 "directions" (the "direction" of time), corresponding to the 1 of the triangle. The dimension 1 (red) has 21 = 2 "directions" (one dimension of space), corresponding to the triangle's 11 line. The dimension 2 (blue) has 22=4 "directions" (two dimensions of space), corresponding to the triangle's 121 line, and the dimension 3 (green) has 23=8 "directions" (three dimensions of space), corresponding to the triangle's 1331 line.
This clarification of our understanding of the dimensions and "directions" of the tetraktys maps directly to those of the LC, as I've shown many times. Hence the mathematics of the expansion of the dimensions of the tetraktys applies to the mathematics of the LC as well:
x = (n0(1x20) + n1(3x21) + n2(3x22) + n3(1x23))
Since the 0, 1, 2 and 3 powers of numbers are here mapped to the 0, 1, 2 and 3 dimensions of the LC spaces, to any number 1, 2, 3, ...n, of the progression, we can see that the long-standing disconnect between the powers of numbers in our algebra and the dimensions of the magnitudes of geometry is vanquished.
This point is made even more clear, when we place the four dimensional progression of the tetraktys and LC on the √1 number line:

Indeed, we can now graph the space/time (time/space) progression of each of the dimensions of the tetraktys and the LC on its own world line chart, which will be shown in due course, but the point to be made here is that the "disaster" Beecham was talking about is the failure to find a particle, a graviton, from which quantum gravity could be generated in the standard model of particle physics.
String theory, on the other hand, could easily provide for gravity and a host of other advances, but not without extending the standard model to include supersymmetric particles (sparticles.) So far, no evidence of the existence of sparticles has been found, at CERN's LHC, but what's more, the easier and less costly search for indirect evidence has dramatically failed as well (see here.)
As they say, however, "one man's trash, is another man's treasure." The indirect evidence of supersymmetry, for which they are so diligently searching, is its inducement of an electric dipole moment in the electron's charge distribution. The fact that they can't find any distortion in the electron's spinning charge that would cause it to deviate from a perfect sphere, only adds to the mystery of the LST's view of the quantum world.
As Einstein reportedly said, "It would be enough for me to understand the electron," or something to that effect. Given the union of algebra and geometry, which we have now found, where the 3d progression defines a continuous ratio of the inner volume of the LC to its outer volume, and knowing that the observed volume of the electron is perfectly spherical, it seems to me that we ought to proceed to the next step by attempting to identify the one with the other.
As the 3d numerical (digital) progression is 8(n3) (or (2n)3), the corresponding continuous progression, given by the ratio of the LC's outer and inner volumes, is n2(√27). Consequently the corresponding continuous magnitude, associated with the numerical 4x4x4 stack of unit cubes (i.e, when n=2), is equal to 22x√27 = √432.
In other words, the S|T unit that makes up the fermions of the first family of our version of the LST's standard model of particle physics (sm), has two units of space oscillation to one unit of time oscillation (S|T=2|1), which, in numerical terms is 64 cubic space units to 8 cubic time units, and in continuous terms is √432 space units to √27 time units.
Understand, the continuous units are given in terms of the ratio of two radii. The 3d outer volume radius, as the numerator and the 3d inner volume unit radius, as the denominator; that is, the ratio of the outer volume radius to the inner volume radius (rov/riv), in both the S and the T oscillations, is taken as the effective radius of the spherical oscillation of the 2nx2nx2n stack of units in each case.
So, because n=2 on the space side of the equation, and n=1 on the time side, in the first family of the sm, rov/riv on the space side is √432, while on the time side it is √27. The difference is the space/time imbalance, or √243, which when multiplied by 3, in the case of the electron, is √2187.
Now, because this is so new to most readers, let me restate the case in terms of the RN number,
S|T = 1/2+1/1+2/1 =4|4 num, [1]
which is sometimes written in a shorthand form as S|T = 1|1.
The first family neutrino and anti-neutrino is made up of three of these,
ν = 3(1/2+1/1+2/1) = (3/6+3/3+6/3) = 12|12 num,
which is a combination of three balanced S|T units; each S|T unit consisting of one space oscillation and one inverse time oscillation. The equation for the electron, on the other hand, consists of three unbalanced S|T units,
e = 3(2/4+2/1+2/1) = (6/12+6/3+6/3) = 18|18 num,
unbalancing the electron equation to its space motion side by three units. For the time oscillation component of the equation, n =1, but for its space oscillation component, n=2 (or S|T=2:1). Numerically, then, the magnitude of the space oscillation is 2(2)x2(2)x2(2) = 4x4x4 = 64 cubic units, while the magnitude of the time oscillation is 2(1)x2(1)x2(1) = 2x2x2 = 8 cubic units. It is this imbalance in the space and time motion that constitutes electric charge.
However, magnitudes of space and time oscillations cannot be measured in terms of cubic units. Therefore, we take the ratio of two radii defined by the stacks of cubes in order to measure the oscillation, or expansion/contraction motion, of the respective stacks. These two radii are the radii of the inner ball that is just contained by the stack and the outer ball that just contains the stack:
re = rov/riv
where re is the effective radius in terms of the outer volume radius (rov) and the inner volume radius (riv) of a given stack. For the 2x2x2 = 8 unit stack, the radius of the inner ball is √1, and the radius of the outer ball is √3. Taking the cube of their ratio, as in the volume formula, we get the square root of 27. As n increases, so does this ratio, so that for any n, the ratio is equal to n2(√27).
Some may be asking, "So what?" at this point. Well, besides showing that continuous magnitudes can correspond to discrete magnitudes, after all, there is also the matter of the electron's "internal clock," which de Broglie pointed out originally, but which the fathers of quantum mechanics ignored. It was termed Zitterbewegung by Schrodinger and forgotten, but Hestenes and others have revived it. See here and here.
In this interpretation of quantum mechanics, the "zitter" motion, as it is sometimes called, is responsible for quantum spin and the magnetic moment of electrons. To quote Hestenes, "The zitter electron is a lightlike charged particle with intrinsic spin that maintains it in a helical spacetime path, with curvature and frequency determined by the electron mass. Thus, electron mass is fully reduced to clock frequency in electron motion." (emphasis added)
Again, scalar motion is out of sight for these people, but unknown to them, we are closing in.
The crux of the problem is the ancient one of squaring the circle. That is, the reconciling of the discrete-based quantum theory with the continuum-based general relativity theory, in order to unify the LST's physical theory - it can't be done and there's proof of that now, but they keep spending billions of dollars trying. What James tells his audience is that when they finally give up trying, it will not be the end of physics, but the beginning.
At that point they will need a fresh approach, one that Peter Woit contends will have to unify LST mathematics with its physics first. I've commented extensively about that over the years, but now that it's apparent that we can unite the algebra of time (or progression) with the algebra of space, to obtain a universal algebra of space/time (time/space), we can legitimately declare that the new beginning of physics has already commenced.
Of course, to convince the skeptics, we need to demonstrate the truth of our unification of numbers of the progression with the right lines and circles of geometry, which I think we can do with the tetraktys and Larson's cube (LC) and the world line chart.
We've already shown how the expansion of the tetraktys follows that of the LC, in 0, 1, 2 and 3 dimensions, since the two are mapped together, we might say. Recall how we identify the binary expansion of the tetraktys with the expansions of the two "directions" of each dimension in Pascal's triangle:

Figure 1. Binary Expansion of Four Dimensions of Tetraktys and Pascal's Triangle
In figure 1 above, the dimension 0 (black) has 20 = 1 "directions" (the "direction" of time), corresponding to the 1 of the triangle. The dimension 1 (red) has 21 = 2 "directions" (one dimension of space), corresponding to the triangle's 11 line. The dimension 2 (blue) has 22=4 "directions" (two dimensions of space), corresponding to the triangle's 121 line, and the dimension 3 (green) has 23=8 "directions" (three dimensions of space), corresponding to the triangle's 1331 line.
This clarification of our understanding of the dimensions and "directions" of the tetraktys maps directly to those of the LC, as I've shown many times. Hence the mathematics of the expansion of the dimensions of the tetraktys applies to the mathematics of the LC as well:
x = (n0(1x20) + n1(3x21) + n2(3x22) + n3(1x23))
Since the 0, 1, 2 and 3 powers of numbers are here mapped to the 0, 1, 2 and 3 dimensions of the LC spaces, to any number 1, 2, 3, ...n, of the progression, we can see that the long-standing disconnect between the powers of numbers in our algebra and the dimensions of the magnitudes of geometry is vanquished.
This point is made even more clear, when we place the four dimensional progression of the tetraktys and LC on the √1 number line:

Indeed, we can now graph the space/time (time/space) progression of each of the dimensions of the tetraktys and the LC on its own world line chart, which will be shown in due course, but the point to be made here is that the "disaster" Beecham was talking about is the failure to find a particle, a graviton, from which quantum gravity could be generated in the standard model of particle physics.
String theory, on the other hand, could easily provide for gravity and a host of other advances, but not without extending the standard model to include supersymmetric particles (sparticles.) So far, no evidence of the existence of sparticles has been found, at CERN's LHC, but what's more, the easier and less costly search for indirect evidence has dramatically failed as well (see here.)
As they say, however, "one man's trash, is another man's treasure." The indirect evidence of supersymmetry, for which they are so diligently searching, is its inducement of an electric dipole moment in the electron's charge distribution. The fact that they can't find any distortion in the electron's spinning charge that would cause it to deviate from a perfect sphere, only adds to the mystery of the LST's view of the quantum world.
As Einstein reportedly said, "It would be enough for me to understand the electron," or something to that effect. Given the union of algebra and geometry, which we have now found, where the 3d progression defines a continuous ratio of the inner volume of the LC to its outer volume, and knowing that the observed volume of the electron is perfectly spherical, it seems to me that we ought to proceed to the next step by attempting to identify the one with the other.
As the 3d numerical (digital) progression is 8(n3) (or (2n)3), the corresponding continuous progression, given by the ratio of the LC's outer and inner volumes, is n2(√27). Consequently the corresponding continuous magnitude, associated with the numerical 4x4x4 stack of unit cubes (i.e, when n=2), is equal to 22x√27 = √432.
In other words, the S|T unit that makes up the fermions of the first family of our version of the LST's standard model of particle physics (sm), has two units of space oscillation to one unit of time oscillation (S|T=2|1), which, in numerical terms is 64 cubic space units to 8 cubic time units, and in continuous terms is √432 space units to √27 time units.
Understand, the continuous units are given in terms of the ratio of two radii. The 3d outer volume radius, as the numerator and the 3d inner volume unit radius, as the denominator; that is, the ratio of the outer volume radius to the inner volume radius (rov/riv), in both the S and the T oscillations, is taken as the effective radius of the spherical oscillation of the 2nx2nx2n stack of units in each case.
So, because n=2 on the space side of the equation, and n=1 on the time side, in the first family of the sm, rov/riv on the space side is √432, while on the time side it is √27. The difference is the space/time imbalance, or √243, which when multiplied by 3, in the case of the electron, is √2187.
Now, because this is so new to most readers, let me restate the case in terms of the RN number,
S|T = 1/2+1/1+2/1 =4|4 num, [1]
which is sometimes written in a shorthand form as S|T = 1|1.
The first family neutrino and anti-neutrino is made up of three of these,
ν = 3(1/2+1/1+2/1) = (3/6+3/3+6/3) = 12|12 num,
which is a combination of three balanced S|T units; each S|T unit consisting of one space oscillation and one inverse time oscillation. The equation for the electron, on the other hand, consists of three unbalanced S|T units,
e = 3(2/4+2/1+2/1) = (6/12+6/3+6/3) = 18|18 num,
unbalancing the electron equation to its space motion side by three units. For the time oscillation component of the equation, n =1, but for its space oscillation component, n=2 (or S|T=2:1). Numerically, then, the magnitude of the space oscillation is 2(2)x2(2)x2(2) = 4x4x4 = 64 cubic units, while the magnitude of the time oscillation is 2(1)x2(1)x2(1) = 2x2x2 = 8 cubic units. It is this imbalance in the space and time motion that constitutes electric charge.
However, magnitudes of space and time oscillations cannot be measured in terms of cubic units. Therefore, we take the ratio of two radii defined by the stacks of cubes in order to measure the oscillation, or expansion/contraction motion, of the respective stacks. These two radii are the radii of the inner ball that is just contained by the stack and the outer ball that just contains the stack:
re = rov/riv
where re is the effective radius in terms of the outer volume radius (rov) and the inner volume radius (riv) of a given stack. For the 2x2x2 = 8 unit stack, the radius of the inner ball is √1, and the radius of the outer ball is √3. Taking the cube of their ratio, as in the volume formula, we get the square root of 27. As n increases, so does this ratio, so that for any n, the ratio is equal to n2(√27).
Some may be asking, "So what?" at this point. Well, besides showing that continuous magnitudes can correspond to discrete magnitudes, after all, there is also the matter of the electron's "internal clock," which de Broglie pointed out originally, but which the fathers of quantum mechanics ignored. It was termed Zitterbewegung by Schrodinger and forgotten, but Hestenes and others have revived it. See here and here.
In this interpretation of quantum mechanics, the "zitter" motion, as it is sometimes called, is responsible for quantum spin and the magnetic moment of electrons. To quote Hestenes, "The zitter electron is a lightlike charged particle with intrinsic spin that maintains it in a helical spacetime path, with curvature and frequency determined by the electron mass. Thus, electron mass is fully reduced to clock frequency in electron motion." (emphasis added)
Again, scalar motion is out of sight for these people, but unknown to them, we are closing in.
Re: Meeting a Terrific Challenge
Thirteen years ago, a paper was submitted to the preprint archive, arXiv, entitled, "Some remarks about mass and Zitterbewegung substructure of the electron." The abstract is interesting:
What's curious about all this is that the electron's charge is attributed to its "zitter" motion, but as Larson pointed out long ago, the LST community has no definition of electrical charge. They can only describe its effects, so when they speak of "charge distribution," it's a distribution of electrical effect. Yet in the RST, we know what charge is. It is a motion, like everything else in the RST universe.
Moreover, we know that the charge distribution, so-called, is perfectly spherical, as discussed in the previous comment above. Of course, if it is this spherical object itself that is oscillating, and its mass "is fully reduced to clock frequency," as Hestenes put it (see end of previous comment,) then the question is, "Why is the up quark more massive than the electron, and the down quark more massive than both of them?"
In the equivalent to the standard model in the LRC's RSt, the charges of the particles result from what Larson called "speed displacement," and it is so in our theory as well, but the basis for his calculation was quite different in his theory than in ours.
In our theory, the total speed displacement attributable to electric charge is three + or - units. These units are measured from the 0 displacement of the neutrino, in two "directions," or polarities. The charge of the down (anti-down) quark consists of one unit of + or - displacement, while the up (anti-up) quark consists of two units of + or - displacement and the electron (positron) consists of three such units.
This is a very powerful ansatz in our theoretical development, because it is so fundamental. As a comparison, we can think of the integer number system, where 4/4 represents the same potential as the swing of a pendulum divided, or quantized, if you will, into six segments. Each division of segments is represented by a displacement in one of two possible "directions," away from the center, or non-displaced position:
1/4, 2/4, 3/4, 4/4, 4/3, 4/2, 4/1
We think of the center, non-displaced, position, of the pendulum (4/4), as the point of zero potential energy and maximum kinetic energy, while the - and + positions at the extremities (1/4 & 4/1), as the positions of maximum potential and zero kinetic energy.
This vibration is the basis of all LST physics, as Einstein. and most others, have observed. However its magnitudes are continuous magnitudes that we have artificially quantitzed with our integers. The desired goal is to understand how nature quantizes the continuum.
Clearly, in an RST-based system, such as ours, the continuum to be quantized is not one of bounded magnitude, but of space/time (time/space) progression, and the educated guess that leads to our ansatz, is the occurrence of periodic "direction" reversals in the progression of one or the other of its two aspects.
Consequently, we can consider our version of the standard model, as the basis of our version of quantum physics, in a manner very similar to the foundational role of the swinging pendulum in classical physics. To do this, we regard our units of space (S) and time (T) oscillation in terms of units of - and + displacement from zero displacement, in the same way we did the pendulum.
Only at the zero, or non-displaced position (4/4), the potential charge is maximum and the actual charge is zero, but at the extremities (1/4 & 4/1), the actual charge is maximum and the potential charge is zero. In other words, potential charge is displaced by actual charge, in our system, just as kinetic energy is displaced by potential energy, in the pendulum system.
On the other hand, unit motion, the inverse of unit mass, in the 3d case at least, is a balance of unit space and unit time oscillation, in the S|T = 1:1 unit. Therefore, one balances, or cancels out, the other, we might say. Even so, unlike in the displacement view, we begin the count with this "c" motion, or 1 at the 4/4 position and count 2 units of motion at the next position (3/4 & 4/3), 3 at the next and 4 at the last.
Although, this doesn't appear to follow the swinging pendulum model, it does, because a 4:4 ratio is effectively zero, and the space/time dimensions are inverted on the other side of unity. So, the charges are additive inverses (or zero sum), while the motions (masses) are multiplicative inverses, but the quantized pendulum analogy holds.
From this perspective, the neutrino is not massless, it's effectively massless, because its space motion is cancelled out by its inverse, time motion. (s3/t3 x t3/s3 = 1.) In reality, the (canceled) mass of the neutrino is the unit mass of our standard model version. It then follows that the down quark and its anti-particle would be 3/4 unit mass, the up quark and its anti-up would be 1/2 unit mass, while the + & - leptons would be 1/4 unit mass, but since this isn't the case, there must be other factors, affecting the mass. For instance, color charge.
Now, this concept is at the root of the LST’s so-called quantum chromodynamics (QCD) theory, used to explain how to account for the masses of the proton and neutron, where the combination of up and down quarks is bound by the "strong interaction" of the "color charges," whose force is much greater and much shorter range than the other two "forces" of the standard model, the weak and electromagnetic (electro-weak) forces.
It turns out that, according to the LST's QCD theory, quarks can be one of three "colors," which are labeled red, blue or green. The color charges have nothing to do with color of course, but the analogy works because combining these three colors produces a white color, just as combining the three different quark charges produces a neutral or balanced strong force between the constituent quarks of the proton and neutron.
Now, there's a further twist in the theory, since most of the mass of the nucleons is not due to the mass of the constituent quarks, but to the energy (mass equivalent) of these color charges of the strong interaction. What's more, the mix of the proton's color charges is slightly less massive than the mix of those of the neutron.
Well, in our RSt, we also have three variations of quarks, as we saw in the penultimate post above, and these variations have to do with the units of the 1, 2 and 3 dimensional scalar math. Recall how there are three integer values, one for each dimensional system: the 1d value = √1, the 2d value = √4, and the 3d value = √9.
Since the nucleons consist of three quarks, two of one variety and one of the opposite variety, if the difference between them is dimensional, then the dimensions of the two identical quarks could be 1d and 2d to oppose and thus balance the scalar motion of the third quark, which would be 3d, and the color analogy would hold.
In the case of the leptons, the 3d value would consist of three 1d values, thus they act as one 3d unit in two, opposite "directions," positive and negative, as observed.
Interestingly enough, there is a slight difference between a native 3d value and the combination of opposing 1d and 2d values, accounting for the slight mass difference of the two nucleons, but more on that later. For now, it's enough to know that perhaps we have something to work with in this regard.
We'll see.
Fifteen years before that, in 1990, David Hestenes published his paper entitled, "The Zitterbewegung Interpretation of Quantum Mechanics," where he used his "geometrically purified" algebra, he called his Space Time Algebra (STA), to reinterpret the Dirac QM equations, showing that the neglected "zitter" motion of the electron, is actually "a ubiquitous phenomena with manifestations in every application of quantum mechanics."It is shown that the electron Zitterbewegung, that is, the high-frequency microscopic oscillatory motion of electron about its centre of mass, originates a spatial distribution of charge. This allows the point-like electron to behave like a particle of definite size whose self-energy, that is, energy of its electromagnetic field, owns a finite value. This has implications for the electron mass, which, in principle, might be derived from Zitterbewegung physics.
What's curious about all this is that the electron's charge is attributed to its "zitter" motion, but as Larson pointed out long ago, the LST community has no definition of electrical charge. They can only describe its effects, so when they speak of "charge distribution," it's a distribution of electrical effect. Yet in the RST, we know what charge is. It is a motion, like everything else in the RST universe.
Moreover, we know that the charge distribution, so-called, is perfectly spherical, as discussed in the previous comment above. Of course, if it is this spherical object itself that is oscillating, and its mass "is fully reduced to clock frequency," as Hestenes put it (see end of previous comment,) then the question is, "Why is the up quark more massive than the electron, and the down quark more massive than both of them?"
In the equivalent to the standard model in the LRC's RSt, the charges of the particles result from what Larson called "speed displacement," and it is so in our theory as well, but the basis for his calculation was quite different in his theory than in ours.
In our theory, the total speed displacement attributable to electric charge is three + or - units. These units are measured from the 0 displacement of the neutrino, in two "directions," or polarities. The charge of the down (anti-down) quark consists of one unit of + or - displacement, while the up (anti-up) quark consists of two units of + or - displacement and the electron (positron) consists of three such units.
This is a very powerful ansatz in our theoretical development, because it is so fundamental. As a comparison, we can think of the integer number system, where 4/4 represents the same potential as the swing of a pendulum divided, or quantized, if you will, into six segments. Each division of segments is represented by a displacement in one of two possible "directions," away from the center, or non-displaced position:
1/4, 2/4, 3/4, 4/4, 4/3, 4/2, 4/1
We think of the center, non-displaced, position, of the pendulum (4/4), as the point of zero potential energy and maximum kinetic energy, while the - and + positions at the extremities (1/4 & 4/1), as the positions of maximum potential and zero kinetic energy.
This vibration is the basis of all LST physics, as Einstein. and most others, have observed. However its magnitudes are continuous magnitudes that we have artificially quantitzed with our integers. The desired goal is to understand how nature quantizes the continuum.
Clearly, in an RST-based system, such as ours, the continuum to be quantized is not one of bounded magnitude, but of space/time (time/space) progression, and the educated guess that leads to our ansatz, is the occurrence of periodic "direction" reversals in the progression of one or the other of its two aspects.
Consequently, we can consider our version of the standard model, as the basis of our version of quantum physics, in a manner very similar to the foundational role of the swinging pendulum in classical physics. To do this, we regard our units of space (S) and time (T) oscillation in terms of units of - and + displacement from zero displacement, in the same way we did the pendulum.
Only at the zero, or non-displaced position (4/4), the potential charge is maximum and the actual charge is zero, but at the extremities (1/4 & 4/1), the actual charge is maximum and the potential charge is zero. In other words, potential charge is displaced by actual charge, in our system, just as kinetic energy is displaced by potential energy, in the pendulum system.
On the other hand, unit motion, the inverse of unit mass, in the 3d case at least, is a balance of unit space and unit time oscillation, in the S|T = 1:1 unit. Therefore, one balances, or cancels out, the other, we might say. Even so, unlike in the displacement view, we begin the count with this "c" motion, or 1 at the 4/4 position and count 2 units of motion at the next position (3/4 & 4/3), 3 at the next and 4 at the last.
Although, this doesn't appear to follow the swinging pendulum model, it does, because a 4:4 ratio is effectively zero, and the space/time dimensions are inverted on the other side of unity. So, the charges are additive inverses (or zero sum), while the motions (masses) are multiplicative inverses, but the quantized pendulum analogy holds.
From this perspective, the neutrino is not massless, it's effectively massless, because its space motion is cancelled out by its inverse, time motion. (s3/t3 x t3/s3 = 1.) In reality, the (canceled) mass of the neutrino is the unit mass of our standard model version. It then follows that the down quark and its anti-particle would be 3/4 unit mass, the up quark and its anti-up would be 1/2 unit mass, while the + & - leptons would be 1/4 unit mass, but since this isn't the case, there must be other factors, affecting the mass. For instance, color charge.
Now, this concept is at the root of the LST’s so-called quantum chromodynamics (QCD) theory, used to explain how to account for the masses of the proton and neutron, where the combination of up and down quarks is bound by the "strong interaction" of the "color charges," whose force is much greater and much shorter range than the other two "forces" of the standard model, the weak and electromagnetic (electro-weak) forces.
It turns out that, according to the LST's QCD theory, quarks can be one of three "colors," which are labeled red, blue or green. The color charges have nothing to do with color of course, but the analogy works because combining these three colors produces a white color, just as combining the three different quark charges produces a neutral or balanced strong force between the constituent quarks of the proton and neutron.
Now, there's a further twist in the theory, since most of the mass of the nucleons is not due to the mass of the constituent quarks, but to the energy (mass equivalent) of these color charges of the strong interaction. What's more, the mix of the proton's color charges is slightly less massive than the mix of those of the neutron.
Well, in our RSt, we also have three variations of quarks, as we saw in the penultimate post above, and these variations have to do with the units of the 1, 2 and 3 dimensional scalar math. Recall how there are three integer values, one for each dimensional system: the 1d value = √1, the 2d value = √4, and the 3d value = √9.
Since the nucleons consist of three quarks, two of one variety and one of the opposite variety, if the difference between them is dimensional, then the dimensions of the two identical quarks could be 1d and 2d to oppose and thus balance the scalar motion of the third quark, which would be 3d, and the color analogy would hold.
In the case of the leptons, the 3d value would consist of three 1d values, thus they act as one 3d unit in two, opposite "directions," positive and negative, as observed.
Interestingly enough, there is a slight difference between a native 3d value and the combination of opposing 1d and 2d values, accounting for the slight mass difference of the two nucleons, but more on that later. For now, it's enough to know that perhaps we have something to work with in this regard.
We'll see.