Page 1 of 1
Inter-Body Stability Distance
Posted: Tue Nov 15, 2016 12:26 pm
by bperet
rossum wrote:I have a solid background in differential equations and solid/fluid dynamics i.e. pressure based systems.
Perhaps you can solve this problem (for a simulation). Gopi has not been able to figure it out--something do to with variables going to infinity.
Given two motions, A and B, expressed as spheres with coordinates that define a center of gravity, having gravitational limits G and masses M (M being the net inward speed):
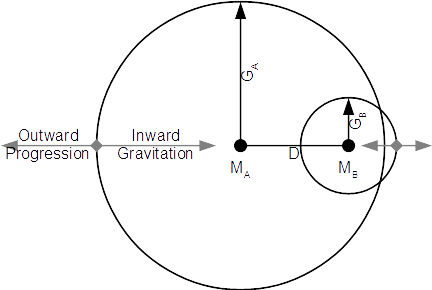
- SphericalBodyProblem.png (22.43 KiB) Viewed 15897 times
All motion outside of the gravitational limit progresses linearly outward at the speed of light. All motion inside the gravitational limit follows the equations of a diminishing spherical surface. Determine an equation to find D, the point of equilibrium.
Though this was done for astronomical applications, it should also work for inter-atomic distances where the center is the net, inward motion from atomic rotation.
Re: Inter-Body Stability Distance
Posted: Tue Nov 15, 2016 2:39 pm
by SoverT
Does this presentation of the problem take into account the idea you mentioned of a Primary and Secondary spatial location? My understanding is still too fuzzy to assess whether that's a relevant factor or not, here.
Re: Inter-Body Stability Distance
Posted: Thu Nov 17, 2016 4:35 am
by rossum
If I understood the problem correctly the answer should be (in arbitrary units)
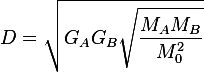 Explanation
Explanation
If all motion outside the gravitational limit progresses outward, it means that on the surface of a ball with radius G the motion should be precisely balanced. So the apparent force exerted by the inward motion (of a body with mass

) should be equal to the force by the natural progression of the system to a body with unit mass

.
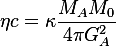
(1)
where
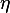
is a conversion factor from motion of natural progression to force or something like viscosity of the natural progression.
The same goes for mass

. For the system of masses

and

it reads:
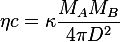
(2)
Now we solve eq (1) for mass A in terms of gravitational limit and ratio of mass A to the unit mass.
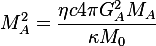
hence

Substituting masses form eq. (3) to eq (2) and solving for D we get
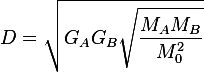
It should be noted that it is independent on the "viscosity" or how much of the progression is felt by the body. Secondly, I don't see here a the problem with the infinities... Where exactly was it?
Re: Inter-Body Stability Distance
Posted: Thu Nov 17, 2016 12:20 pm
by bperet
SoverT wrote:Does this presentation of the problem take into account the idea you mentioned of a Primary and Secondary spatial location? My understanding is still too fuzzy to assess whether that's a relevant factor or not, here.
This would be "primary location" in space only. I needed a verifiable starting point before I added in the secondary location and the temporal locations.
The primary and secondary locations are analogous to the concepts of primary and secondary mass, as well as principle and subordinate rotations. When you make the RS perfectly symmetric in space and time, everything seems to come in pairs.
Re: Inter-Body Stability Distance
Posted: Thu Nov 17, 2016 12:23 pm
by bperet
rossum wrote:It should be noted that it is independent on the "viscosity" or how much of the progression is felt by the body. Secondly, I don't see here a the problem with the infinities... Where exactly was it?
I emailed Gopi and asked that he take a look at this and explain the problem he was having. I recall he was using logarithms, not roots.
Let me think about the viscosity concept--I believe sphere B would appear to be in a viscous liquid because it is wanting to progress outward at the same time A is pulling it inward. That would appear as a resistance.
Re: Inter-Body Stability Distance
Posted: Sun Nov 20, 2016 12:18 pm
by Gopi
The trouble I was running into was the behavior of time inside and outside the bubble. If time is kept at a constant flow, then it reduces to a problem of algebra, as you showed, rossum. That was leading me to logs.
Second trouble was, as I was bringing the two bubbles into contact, the bubbles themselves were distorting (because equilibrium shifts). That makes them different from a regular rigid sphere with rigid outline, since all boundaries are dependent on equilibrium of forces. Changes all values of radii etc.
Re: Inter-Body Stability Distance
Posted: Sat Nov 26, 2016 10:53 am
by rossum
Gopi wrote:Second trouble was, as I was bringing the two bubbles into contact, the bubbles themselves were distorting (because equilibrium shifts). That makes them different from a regular rigid sphere with rigid outline, since all boundaries are dependent on equilibrium of forces. Changes all values of radii etc.
There are standard numerical methods to deal with it (when algebra fails). Please include details so I can post some suggestions on how to do it. If possible please explain how and why is the radius changing in as much detail as possible.
I would be also grateful if you could post here the attempt on this with the logs. It could give me more idea on how it could be solved.
Thanks in advance