In our RSt, where the unit of elementary scalar motion from which higher combinations are derived, the S|T unit, is an oscillating volume of space and time, understanding what accounts for the observed atomic energy transitions in the combinations identified as atoms is not easy.
This is especially challenging given that, in our theory, the electron has no identity and consequently no properties, as an electron, until it is created in the disintegration of the atom, or in the process of its ionization. Fortunately, however, we have the scalar motion equation to help.
Recall, that the basic scalar motion equation is,
S|T = 1/2+1/1+2/1 = 4|4 num (natural units of motion),
And our basic energy, or inverse motion equation is,
T|S = 1/2+1/1+2/1 = 4|4 num (natural units of inverse motion),
Now, this terminology and notation will be a complete mystery to those who have not read the previous posts, so reading and understanding those posts first is a prerequisite for the study of what follows, and while we are on the subject, let me emphasize the tentative nature of all the conclusions presented thus far. It may be necessary to eat a lot of humble pie from time to time, during the development of our RSt, for several reasons, but if so, it won't be the first time. It has been said before and bears repeating: It takes courage to develop a physical theory, not to mention a new system of physical theory. Larson was an incredibly courageous man, as well as an intelligent and honest investigator. Perhaps those of us who try to follow his lead appreciate that fact more than most.
With that said, we have taken on the challenge of dealing with units of energy, with dimensions E=t/s, as well as motion, with dimensions v=s/t, and have dared to cross over the line of LST physics, which cannot brook the existence of entities over the speed of light, which are known as "tachyons," in that system. Nevertheless, the T units in our RSt are just such units, but because the dimensions of these units are actually the inverse of less than unit speed units, no known laws of LST physics are broken.
In retrospect, venturing into this unexplored realm of apparent over-unity, which seems so iconoclastic, appears to be the natural and compelling evolution of physical thought. So much so that one marvels that the world had to wait so long for the Columbus-like pioneer Larson to show science the way. However, incredible as it is, the entire LST community, save just a few, has no idea yet that our understanding of the nature of space and time has been revolutionized. They cannot, as yet, recognize that time is the inverse of space, even though it's as plain as the nose on your face, as soon as someone points out how it can be.
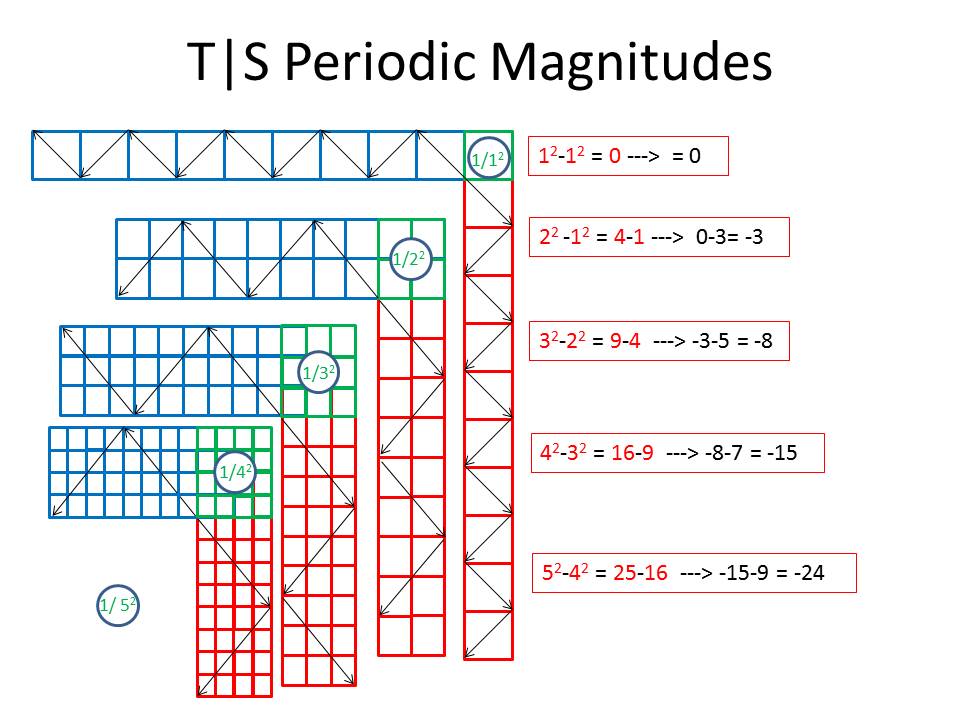
By the same token, the mathematics of the new system is just as iconoclastic. As we consider the basic scalar motion equation, n(S|T)=n4|n4, and its inverse, n(T|S)=n4|n4, and graph their simple magnitudes, we find that its also possible to formulate a basic scalar energy equation, where
S*T = n2.
In the previous posts above, I've explained how S|T units combine into entities identified with the observed first family of the LST's standard model (sm), and these combos combine into entities that are identified as protons and neutrons, which combine into elements of the periodic table, or Wheel of Motion:
The symbolic representation of the S|T units that, as preons, combine to form the fermions and bosons of our RSt, are a reflection of the S|T equation, making it possible to graphically represent them and their combinations as protons and neutrons along with their respective magnitudes of natural units of motion. On this basis, the S|T magnitudes for the proton, neutron and electron combos are:
P = 46|46 num,
N = 44|44 num,
E = 18|18 num
The magnitude of the Hydrogen atom (Deuterium isotope) is then the sum of these three:
H = 46+44+18 = 108|108 num.
At this point, however, representing the constituents of the atom as combos of S|T triplets (see previous posts above), becomes cumbersome and we need to condense the symbols from 20 triangles to 4 triangles, in the form of a tetrahedron, as shown below:
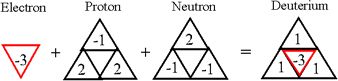
The top triangle of the tetrahedron is the odd man out for the nucleons, so that for the proton this is the down quark, but for the neutron it is the up quark.
The numbers in the four triangles are the net magnitudes of the quarks and the electron. So, the number of the down quark at the top of the proton is -1, because the magnitude of the inner term of its S|T equation is 2/1, (-2+1 = -1), whereas the number of its two up quarks is 2, because the inner terms of their S|T equations are both 3/5, (-3+5=2). For the neutron, the number of the single up quark at the top is 2, while the magnitude of the two down quarks below it is -1, given the inner terms of their S|T equations.
The inner term of the electron's S|T equation is 6/3, or -3, (-6+3=-3), so that the net motion of the three entities combined as the Deuterium atom balance out at 3-3 = 0, or neutral in terms of charge, as show in the graphic above.
In this way, each element of the Wheel could be represented by the numbers of its tetrahedron symbol, if there were some need to do so, but what is more useful is the S|T equation itself. Expanding the equation for Deuterium:
D = 27/54+27/27+54/27 = 108|108 num,
but factoring out 33, we get:
D = 33(1/2+1/1+2/1) = 108|108 num.
To take advantage of this factorization we can represent it by making the S|T symbols of the notation bold:
S|T = 33(1/2+1/1+2/1) = 108|108 num
Hence,
D = S|T= 108; He = 2(S|T) = 216; Li = 3(S|T) = 324, etc.
This way, we can easily write the S|T equation for any element, X, given its atomic number, Z:
XZ = z(S|T)
However, while this should prove to be quite helpful as compact notation, there is still more to consider. Recall that the units on the world-line chart actually represent the expanding/contracting radius of an oscillating volume, and as such, its magnitude is the square root of 3, not 1. This factor expands the relative magnitudes involved considerably, which we will investigate more later on.
For now, I want to draw your attention to the scalar energy equation,
S*T = n2.
Recall that for the S*T unit,
S*T = 1/(n+1) * (n*n) * (n+1)/1 = n2,.
So when n = 1,
S*T = (1/2)*(1*1)*(2/1) = ((1/2)(2/1)(1*1)) = ((2/2)(1*1)) = 1*1 = 12,
but, if we invert the multiplication operation, we get:
S/T = (1/2)/(1/1)/(2/1) = ((1/2)(1/1))(1/2) = (1/2)(1/2) = 1/22,
which we want to do when we wish to view the S&T cycles, in terms of energy, so that:
E = hv ---> T/S = 1/S/T = n2,
where n is the number of cycles in a given S|T unit.
Now, this may seem to be contrived, and perhaps it is, especially when we invert the operation of the inner term of the S*T equation from division (n/n) to multiplication (n*n). However, if we don't invert it, the equation will always equal 1, while if we do invert it, then dividing 'T' cycles, by 'S' cycles (T/S) yields the correct answer, T/S = n2.
Now, this brings us to something else that needs to be clarified. In the chart showing the correlation between the quadratic equation of the S|T units and the line spectra of Hydrogen, given the Rydberg equation, the frequency of the S|T units is shown as decreasing with increasing energy, rather than increasing as it should. This is problematic to say the least, but I think it can be resolved, when we consider that the "direction" reversals of each S and T unit always remains at the 1/2 and 2/1 ratio, even though their combined magnitude is greater in the absolute sense; that is, while the space/time (time/space) ratio of 1/2, 2/4, 3/6, 4/8, ...n/2n, remains constant at n/2n = 1/2, the absolute magnitude of 2n - n increases, as n: 1, 2, 3, 4, ...2n-n.
Therefore, the length of the reversing "direction" arrows, shown in the graphic, as increasing in length, as the absolute magnitude increases, is an incorrect representation of the physical picture. The correct representation would show the number of arrows increasing, as S|T units are combined, with their lengths (i.e.their periods) remaining constant, so that, as the quadratic energy increases, the number of 1/2 periods in a given S|T combo increases. The frequency of the unit then is that of a frequency mixer, containing both the sum and difference frequencies of its constituent S|T units..
Of course, this is not exactly what is observed, but upon further investigation, we may be able to resolve the discrepancy. At least it is consistent with our theoretical development.
In the meantime, for the energy conversion of the S|T equation of the Hydrogen atom, where n = 1, with 33 factored out, we get:
S/T = (1/33n)2 = 1/272, and T/S = (33n)2 = 272 = 729,
when we put the 33 factor back in, so we get the actual number of 1/2 and 2/1 cycles, or S and T units, contained in the Hydrogen atom.
There are a lot of tantalizing clues to follow in the investigation of these equations and their relation to the conventions of the LST particle physics community, which uses units of electron volts for energy, dividing those units by the speed of light to attain units of momentum, and dividing them by the speed of light squared to attain units of mass. They even divide the reduced Planck's constant by eV to attain a unit of time, and that result times c to get the unit of space, according to Wikipedia:
Measurement--Unit---------SI value of unit
Energy----------eV--------------1.602176565(35)×10−19 J
Mass------------eV/c2-----------1.782662×10−36 kg
Momentum-----eV/c ------------5.344286×10−28 kg⋅m/s
Time-------------ħ/eV------------6.582119×10−16 s
Distance---------ħc/eV----------1.97327×10−7 m
It'll take a while to untangle these units and see how they correspond to the S|T units of motion, but in the meantime, we can use the progress achieved so far to analyze the periodic table of elements, showing why Larson's four, 4n2, periods define it, using the LRC model of the atom explained so far.