The LST community views the physical universe as a stage of space and time for matter and its interactions. As David Hestenes expresses it, the goal of their research program is to find the set of the fewest interactions among the set of the fewest particles of nature, This has resulted in the standard model of particle physics.
Larson's program of research is radically different. It assumes that everything in the physical universe stems from the reciprocal relation between space and time, which it assumes exists in discrete units of three dimensions. This has led us to deduce that, instead of adding time as a fourth dimension to the Pythagorean theorem equation, which is the basis for the LST community's concept of spacetime, we conceive of two separate Pythagorean equations, one for space and one for time, each with three dimensions. which are reciprocals.
The equation of space, √(12 + 12 + 12) = √3, is calculated from the LC in units of space, while the equation of time is the inverse of this, 1/√(12 + 12 + 12) = 1/√3, calculated from the LC in units of time. The respective volumes of space and time associated with each of these equations for their respective radii are inverse, and the space volume is calculated to be 27 times smaller than the time volume.
For unknown reasons, this value coincides with the value of the number of poles in the 3d space calculated from the tetraktys:
0d = 30 = 1
1d = 31 = 3
2d = 32 = 9
3d = 33 = 27
when the coefficients of the binomial expansion equation of the tetraktys (see Pascal's triangle) are taken into account, which, for three dimensions, are 1, 3, 3, and 1. Now, the question is, how do we calculate the number of poles for the inverse tetraktys, the tetraktys of time, we might say? Do we just invert the numbers:
1/0d = 1/30 = 1/1
1/1d = 1/31 = 1/3
1/2d = 1/32 = 1/9
1/3d = 1/33 = 1/27
This seems logical, but who has ever heard of inverse dimensions? Nevertheless, when we calculate the number of poles in our revised "Bott clock" we get:
0d = 34 = 81
1d = 35 = 243
2d = 36 = 729
3d = 37 = 2187
which numbers, at first glance, look nothing like the inverse dimensional numbers. However, notice that, if we take the 34 = 81 value of poles as the new unit, as indicated should be the case in our "clock," and make it the inverse of the first tetraktys, as also indicated in our "clock," we get the exact inverse of the number of poles in the first tetraktys:
1/0d = 81/81 = 1/1
1/1d = 81/243 = 1/3
1/2d = 81/729 = 1/9
1/3d = 81/2187 = 1/27
The question is now, of course, is this just a little mathematical sleight of hand on our part? Is the logic twisted to suit our objective? The reader will have to make that decision, but I find it hard to believe that we could continue to make these observations by virtue of mere coincidence.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
When we mess with the foundation of mathematics, we mess with the foundation of physics and the technology that is the foundation of Western civilization. God have mercy on my soul, because I can't stop now!
The posts on page 3 of this topic deal with the relationship between the tetraktys and the LC and its consequences. The major conclusion is that the tetraktys is as far as we can take the binomial expansion. There are no higher dimensions in physical phenomena, in spite of Clifford algebra.
Notwithstanding this apparent fact, we've seen how John Baez et. al, explain incredibly complex mathematics in an attempt to go beyond three dimensions (four counting 0). It is very interesting to see how they have mistaken the "directions" of dimensions, or at least mis-labeled them, so that it's difficult to not confuse non-specialists with their mathematical and geometrical concepts.
Nevertheless, the "Bott clock," which we have revised (see previous posts above), helps us to understand the new scalar concepts tremendously, I think, even though it still lacks the clear connection with the LC. I think I can add that too to the clock.
On page 3 of this topic I show how the number 8 of the 3d expansion follows the expansion of the LC: 23, 43. 63, ...2n3.
This connection of numbers and geometry is real easy to show, when n = 1, because the 3d expansion generates the 2x2x2 stack of 8, 1-unit cubes of the LC, which contains all the dimensional sub-spaces of the LC, and the numbers of Pascal's triangle, which are just the coefficients of the binomial expansion (1 3 3 1), at the 3d (fourth) level.
However, if there really are no higher dimensions than these three (four), then how do we modify the binomial expansion to follow the geometric expansion of the LC? The clue is found in the LC expansion, which is actually a cubic expansion, when period 8 is taken into account; that is,
8/8 = 13, 64/8 = 23, 216/8 = 33, ...(2n)3/23 = n3.
Fortunately, this means that n3 is a factor in the third dimension, implying that n2, n1 and n0 are also factors in their respective subspaces of the tetraktys:
20 x n0; 21 x n1; 22 x n2; 23 x n3 = 20; 21; 22; 23, which, when multiplied by their respective binomial coefficients, 1, 3, 3, and 1, produces the LC, when n = 1:
1 monopole, 3 dipoles, 3 quadrupoles, 1 octupole = 27 poles
When n = 2, we get 125 poles, and 3 gives us 343, 4 gives 729 and 5 generates 1331 (just a coincidence, I think). The interesting thing is that these products and sums also form a cubic progression, starting with n =1 ----> 33 = 27:
n = 2 ----> 53; n = 3 ----> 73; n = 4 ----> 93; n = 5 ----> 113. This is an important factor relative to the atomic spectra, but more on that later. Right now, I want to incorporate this into our Bott clock:
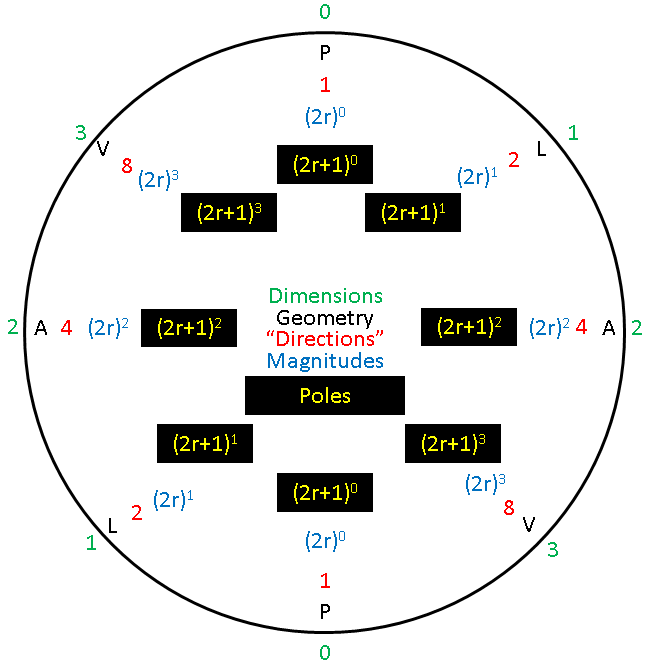
Poles are an alternate way of thinking of magnitudes in two "directions" from a center point:
30 = (1) point:
o
31 poles = 2 end and 1 center point arranged to form a line :
<----o---->
32 poles = 6 end and 3 center points arranged to form an area:
<----o---->
<----o---->
<----o---->
33 poles = 18 end and 9 center points arranged to form a volume:
<----o----> <----o----> <----o---->
<----o----> <----o----> <----o---->
<----o----> <----o----> <----o---->
When n = 5:
<---<---o--->--->
When n = 7:
<---<---<---o--->--->--->
In the case of the clock, n = r, so that for each r = 1, 2, 3, … n, there is a dual set of tetraktii generated, each corresponding to its respective LC.
This is much easier to work with than thinking that the dimensions can be incremented higher and higher, as in the fourth dimension and beyond of Clifford algebras:

The posts on page 3 of this topic deal with the relationship between the tetraktys and the LC and its consequences. The major conclusion is that the tetraktys is as far as we can take the binomial expansion. There are no higher dimensions in physical phenomena, in spite of Clifford algebra.
Notwithstanding this apparent fact, we've seen how John Baez et. al, explain incredibly complex mathematics in an attempt to go beyond three dimensions (four counting 0). It is very interesting to see how they have mistaken the "directions" of dimensions, or at least mis-labeled them, so that it's difficult to not confuse non-specialists with their mathematical and geometrical concepts.
Nevertheless, the "Bott clock," which we have revised (see previous posts above), helps us to understand the new scalar concepts tremendously, I think, even though it still lacks the clear connection with the LC. I think I can add that too to the clock.
On page 3 of this topic I show how the number 8 of the 3d expansion follows the expansion of the LC: 23, 43. 63, ...2n3.
This connection of numbers and geometry is real easy to show, when n = 1, because the 3d expansion generates the 2x2x2 stack of 8, 1-unit cubes of the LC, which contains all the dimensional sub-spaces of the LC, and the numbers of Pascal's triangle, which are just the coefficients of the binomial expansion (1 3 3 1), at the 3d (fourth) level.
However, if there really are no higher dimensions than these three (four), then how do we modify the binomial expansion to follow the geometric expansion of the LC? The clue is found in the LC expansion, which is actually a cubic expansion, when period 8 is taken into account; that is,
8/8 = 13, 64/8 = 23, 216/8 = 33, ...(2n)3/23 = n3.
Fortunately, this means that n3 is a factor in the third dimension, implying that n2, n1 and n0 are also factors in their respective subspaces of the tetraktys:
20 x n0; 21 x n1; 22 x n2; 23 x n3 = 20; 21; 22; 23, which, when multiplied by their respective binomial coefficients, 1, 3, 3, and 1, produces the LC, when n = 1:
1 monopole, 3 dipoles, 3 quadrupoles, 1 octupole = 27 poles
When n = 2, we get 125 poles, and 3 gives us 343, 4 gives 729 and 5 generates 1331 (just a coincidence, I think). The interesting thing is that these products and sums also form a cubic progression, starting with n =1 ----> 33 = 27:
n = 2 ----> 53; n = 3 ----> 73; n = 4 ----> 93; n = 5 ----> 113. This is an important factor relative to the atomic spectra, but more on that later. Right now, I want to incorporate this into our Bott clock:

Poles are an alternate way of thinking of magnitudes in two "directions" from a center point:
30 = (1) point:
o
31 poles = 2 end and 1 center point arranged to form a line :
<----o---->
32 poles = 6 end and 3 center points arranged to form an area:
<----o---->
<----o---->
<----o---->
33 poles = 18 end and 9 center points arranged to form a volume:
<----o----> <----o----> <----o---->
<----o----> <----o----> <----o---->
<----o----> <----o----> <----o---->
When n = 5:
<---<---o--->--->
When n = 7:
<---<---<---o--->--->--->
In the case of the clock, n = r, so that for each r = 1, 2, 3, … n, there is a dual set of tetraktii generated, each corresponding to its respective LC.
This is much easier to work with than thinking that the dimensions can be incremented higher and higher, as in the fourth dimension and beyond of Clifford algebras:

Re: Meeting a Terrific Challenge
In the previous post, we saw how the progression of physical dimensions is limited to three non-zero dimensions, and how these four (counting zero) relate to the geometric progression of the LC in two numeric progressions. The first is (2n)3, which we can label as the stack number. It counts the number of 3d cubes in the successive stacks of cubes: 8, 64, 216, ....(2n)3 of the progression.
The second geometric progression, which we can call the pole number, is (2n+1)3. It counts the number of poles in a given stack number. Now ignoring for the moment that nature does not expand in cubes (unfortunately), what we want to do is relate these two progressions to the atomic spectra and the elements of the periodic table, in terms of our new scalar motion equation, S|T = (1/2+1/1+2/1) = 4|4. in such a way as to derive a new atomic model of the atom.
The first step is to clarify the fact that our revised Bott clock is not a clock at all. Rather, it is an expansion (appropriately enough) of a radius, r, where r is a natural number (r = 1, 2, 3, ...∞). The expansion generates the two, reciprocal, pole numbers and the two, reciprocal, stack numbers, for a given radius, r. It also generates the corresponding scalar equation for the combination of the two, reciprocal values, since it turns out that the appropriate num of the corresponding scalar equation is just a product of r and the unit num of the scalar equation: or r(4|4).
Recall that the natural units of motion (num) are an unusual combination of space and time oscillations. They are actually space (time) | time (space) ratios, or magnitudes of speed, but hardly in the ordinary sense of that word. As oscillations, they are a measure of frequency, but since they propagate relative to matter, they may be characterized as a combination of a wavelength and a waveduration, where the former can be expressed in terms of rotation, or cycles per unit time, 1/t (change in space-volume over time), and likewise for the latter, as cycles per unit space, or 1/s (change of time-volume over space). Both expressions are "frequencies," but one is an expression of cycles per unit time, while the other is an expression of cycles per unit space, and the cycles are 3d cycles of expansion/contraction, equivalent to 4π, 2d rotations.
The image below shows this Bott expansion graphically, with the stack numbers, pole numbers and respective num contained within concentric circles of radius r:
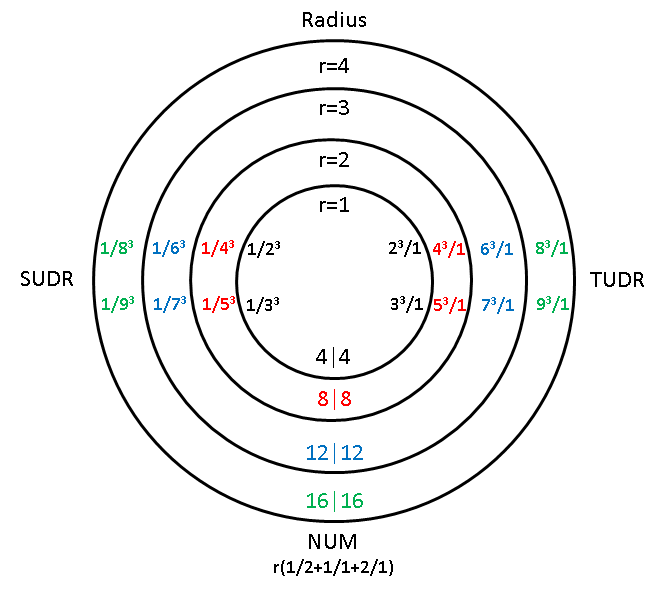
The fact that the concentric circles of the graphic above resemble the 4n2 periods of our Wheel of Motion version of the Periodic Table of Elements is no accident. Notice that the quotient of the num (natural units of motion) values of the scalar motion equation and the total number of cubes (2r)3, in each circle, corresponds to 2(2r2), disregarding that one side is the inverse of the other side:
8/4 = 2; 1/8 ÷1/4 =1/2
64/8 = 8; 1/64 ÷1/8 = 1/8
216/12 = 18; 1/216 ÷1/12 = 1/18
512/16 = 32; 1/512 ÷1/16 = 1/32
This result is very interesting. It seems to indicate that the dual, (2n)2, periodic pattern of the elements follows the pattern of the spectral tetraktys and the Bott expansion, where one-half of the elements in a given period are the inverse of the other half (at least in terms of our scalar equation), even though the number of nucleons and electrons increases linearly with each additional atom in the series.
Moreover, as it turns out, if we multiply the scalar equation by 2r-1, we get the Bott spread of the atomic spectra groups directly, when r runs from 1 to 4:
r=1: (2r-1)(1/2+1/1+2/1) = 1(4|4) ~ 4;
r=2: (2r-1)(1/2+1/1+2/1) = 3(4|4) ~ 12;
r=3: (2r-1)(1/2+1/1+2/1) = 5(4|4) ~ 20;
r=4: (2r-1)(1/2+1/1+2/1) = 7(4|4) ~ 28;
Again, this seems to indicate that there is a connection between these various aspects of our scalar magnitude combinations and the dimensions of the atomic spectra and the periodic table of elements, but exactly what it is remains unclear, as yet.
The second geometric progression, which we can call the pole number, is (2n+1)3. It counts the number of poles in a given stack number. Now ignoring for the moment that nature does not expand in cubes (unfortunately), what we want to do is relate these two progressions to the atomic spectra and the elements of the periodic table, in terms of our new scalar motion equation, S|T = (1/2+1/1+2/1) = 4|4. in such a way as to derive a new atomic model of the atom.
The first step is to clarify the fact that our revised Bott clock is not a clock at all. Rather, it is an expansion (appropriately enough) of a radius, r, where r is a natural number (r = 1, 2, 3, ...∞). The expansion generates the two, reciprocal, pole numbers and the two, reciprocal, stack numbers, for a given radius, r. It also generates the corresponding scalar equation for the combination of the two, reciprocal values, since it turns out that the appropriate num of the corresponding scalar equation is just a product of r and the unit num of the scalar equation: or r(4|4).
Recall that the natural units of motion (num) are an unusual combination of space and time oscillations. They are actually space (time) | time (space) ratios, or magnitudes of speed, but hardly in the ordinary sense of that word. As oscillations, they are a measure of frequency, but since they propagate relative to matter, they may be characterized as a combination of a wavelength and a waveduration, where the former can be expressed in terms of rotation, or cycles per unit time, 1/t (change in space-volume over time), and likewise for the latter, as cycles per unit space, or 1/s (change of time-volume over space). Both expressions are "frequencies," but one is an expression of cycles per unit time, while the other is an expression of cycles per unit space, and the cycles are 3d cycles of expansion/contraction, equivalent to 4π, 2d rotations.
The image below shows this Bott expansion graphically, with the stack numbers, pole numbers and respective num contained within concentric circles of radius r:

The fact that the concentric circles of the graphic above resemble the 4n2 periods of our Wheel of Motion version of the Periodic Table of Elements is no accident. Notice that the quotient of the num (natural units of motion) values of the scalar motion equation and the total number of cubes (2r)3, in each circle, corresponds to 2(2r2), disregarding that one side is the inverse of the other side:
8/4 = 2; 1/8 ÷1/4 =1/2
64/8 = 8; 1/64 ÷1/8 = 1/8
216/12 = 18; 1/216 ÷1/12 = 1/18
512/16 = 32; 1/512 ÷1/16 = 1/32
This result is very interesting. It seems to indicate that the dual, (2n)2, periodic pattern of the elements follows the pattern of the spectral tetraktys and the Bott expansion, where one-half of the elements in a given period are the inverse of the other half (at least in terms of our scalar equation), even though the number of nucleons and electrons increases linearly with each additional atom in the series.
Moreover, as it turns out, if we multiply the scalar equation by 2r-1, we get the Bott spread of the atomic spectra groups directly, when r runs from 1 to 4:
r=1: (2r-1)(1/2+1/1+2/1) = 1(4|4) ~ 4;
r=2: (2r-1)(1/2+1/1+2/1) = 3(4|4) ~ 12;
r=3: (2r-1)(1/2+1/1+2/1) = 5(4|4) ~ 20;
r=4: (2r-1)(1/2+1/1+2/1) = 7(4|4) ~ 28;
Again, this seems to indicate that there is a connection between these various aspects of our scalar magnitude combinations and the dimensions of the atomic spectra and the periodic table of elements, but exactly what it is remains unclear, as yet.
Re: Meeting a Terrific Challenge
Having tied together the expansions of the magnitudes, the dimensions and the "directions" of the tetraktys, the LC and the new scalar motion equation in the previous post, through the mathematical concept of Bott periodicity, by adapting the "Bott clock" from John Baez's post on Bott periodicity, we are now ready to take the next step and apply it (our Bott expansion) to the periodic table of elements.
It happens to work out great, with one caveat: We have to accept that the elements of the two, 2n2 sub-periods, of the 4n2 periods, are reciprocals of each other. This is not surprising news for a reciprocal system theory, but it's undoubtedly a hard pill to swallow for the LST community.
I'm not sure I've got it right, and like our version of the standard model of particle physics, there's a long way to go yet. However, no pain, no gain, so here goes.
Recall from the previous posts, that as the radius r, of the Bott expansion increases from 1 to 4, the magnitudes, defined mathematically by the dimensions and "directions" of the tetraktys, and geometrically by the LC, increase in two, reciprocal "directions," just as the number line of our familiar family of rational numbers does: 1/n, ...1/3, 1/2, 1/1, 2/1, 3/1, ...n/1. The difference is, of course, the Bott expansion is multi-dimensional.
The interesting discovery is that, taking the three-dimensional component of the expansions, enables us to draw a corollary between this series of expansions and the combinations of SUDRs and TUDRs (Ss and Ts), making up our new scalar motion equation, S|T (T|S) = 1/2 + 1/1 + 2/1 = 4|4, which is a scalar motion sum of the total cycles of the space and the time oscillations, for a given value of the Bott expansion radius, r. When we multiply this equation by r = 1 - 4, we get:
1(4|4) = 4|4;
2(4|4) = 8|8;
3(4|4) = 12|12;
4(4|4) = 16|16;
Remarkably, however, when we divide the corresponding number of the Bott LC expansion, 2n3, by these S|T and T|S numbers (the pipe symbol denotes the reciprocity of space and time oscillations), we get the number of elements in the corresponding sub-period of the periodic table:
8/4 = 2;
64/8 = 8;
216/12 = 18;
512/16 = 32;
Given that the RHS side of 4|4 is the reciprocal of the LHS, and the two LC expansions from the Bott expansion are also reciprocals, we seem justified in dividing the reciprocals as well. That is:
1/8 ÷ 1/4 = 1/2;
1/64 ÷ 1/8 = 1/8;
1/216 ÷ 1/12 = 1/18;
1/512 ÷ 1/16 = 1/32,
giving us the number of elements in the two sub-periods in each period of the periodic table, although in reciprocal form. Could it be that the fact that each 4n2 period consists of two 2n2 sub-periods, is due to one sub-period being the reciprocal of the other sub-period, just as in the Bott expansion and the scalar motion equation???
Though skeptical for weeks now, I decided to assume that the stack number (the number of cubes in a 2r3 stack of unit cubes), represents the limit of the number of r(4|4) units of natural scalar motion that can be accommodated for a given expansion of radius r. I really can't say that I understand a physical reason for this yet, but, intuitively, it seems likely. So, I went ahead and worked it out, as shown in the series of graphics below:
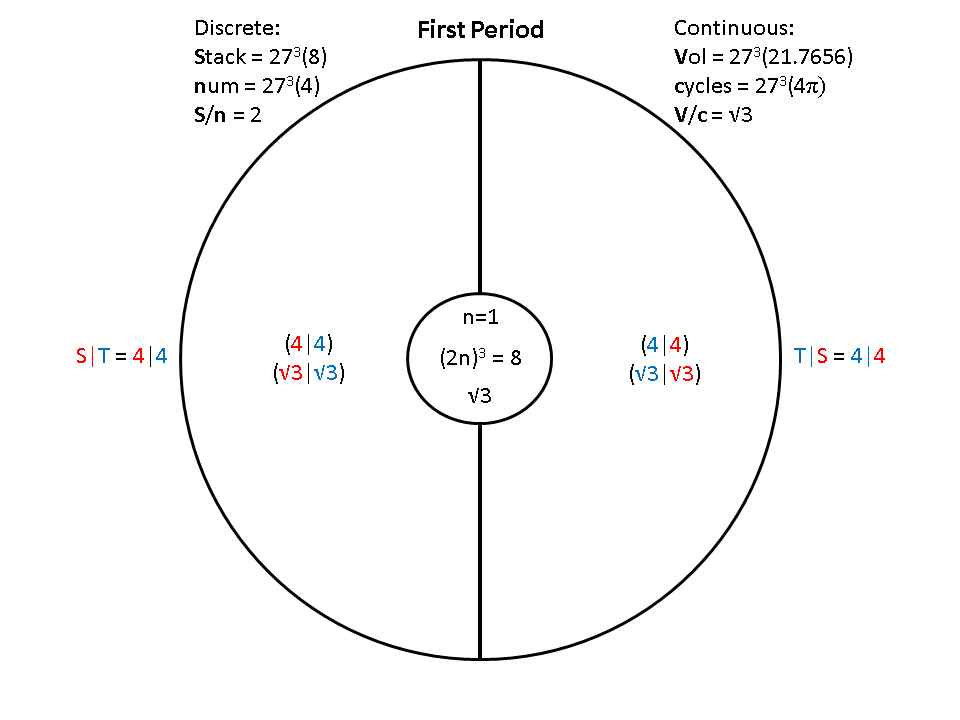
When r = 1, LC = 8, num = 4|4, resulting in two, reciprocal, sub-periods, with one element each: Hydrogen and Helium and one sub-element each.
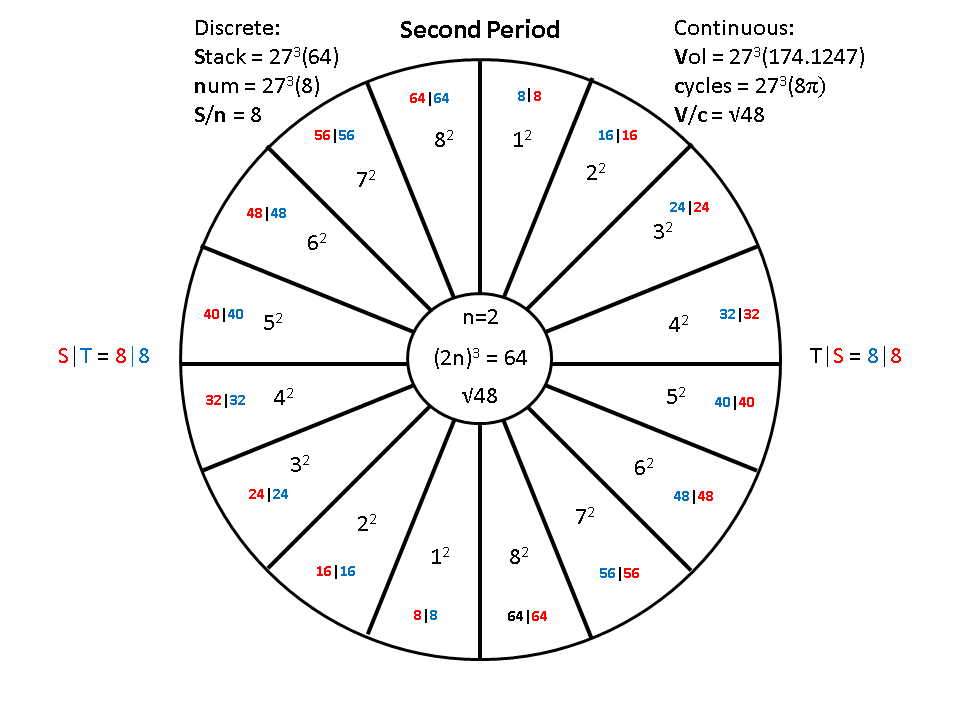
When r = 2, LC = 64, num = 8|8, resulting in two, reciprocal, sub-periods, with eight elements each.
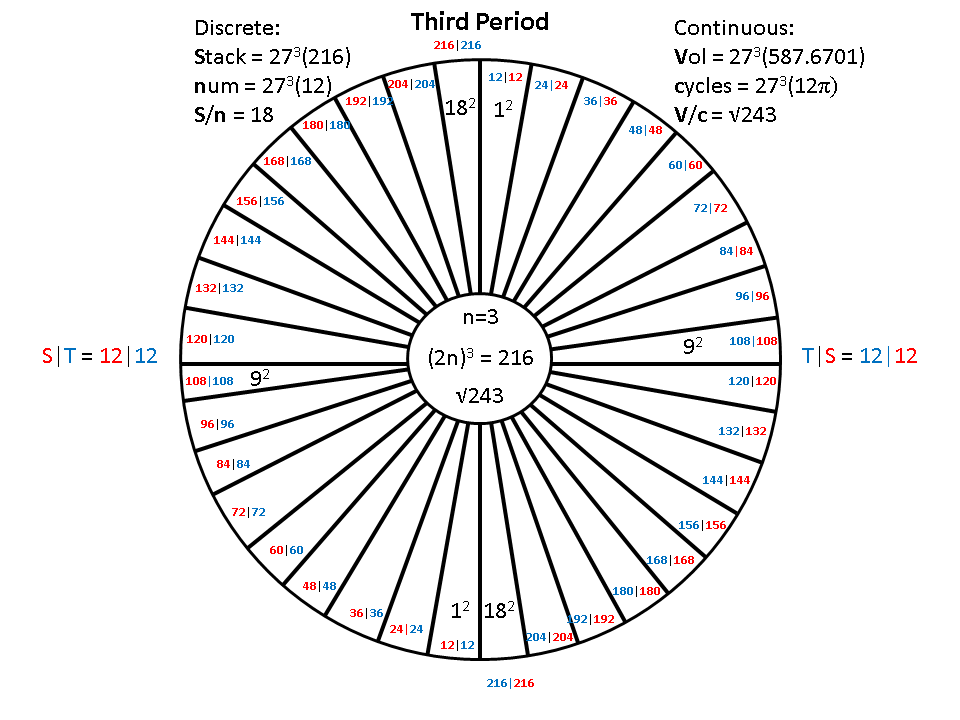
When r = 3, LC = 216, num = 12|12, resulting in two, reciprocal, sub-periods, with eighteen elements each.
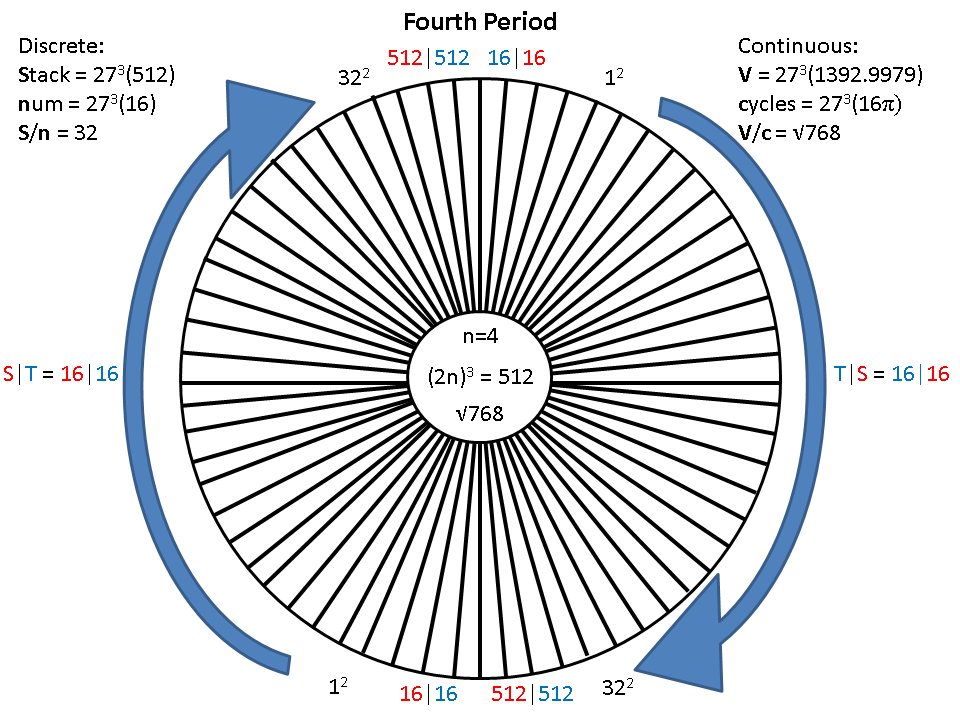
When r = 4, LC = 512, num = 16|16, resulting in two, reciprocal, sub-periods, with thirty two elements each.
Now, this is an encouraging development, but, unfortunately, nature doesn't expand in cubes, and the scalar motion equation for the first atom, Hydrogen, has a total num of 108|108, and subsequent atoms are multiples of this value. However, since the equation for Hydrogen is 27/54+27/27+54/27 = 108|108, we can factor out this value to simplify to 27(1/2 + 1/1+2/1) = 27(4|4), although I don't show this factorization in the graphics above.
The most important implication of this result is that, if it proves valid, we now have a model of the atom for our RSt, which is based on the logical and mathematical progression of multi-dimensional numbers.
It happens to work out great, with one caveat: We have to accept that the elements of the two, 2n2 sub-periods, of the 4n2 periods, are reciprocals of each other. This is not surprising news for a reciprocal system theory, but it's undoubtedly a hard pill to swallow for the LST community.
I'm not sure I've got it right, and like our version of the standard model of particle physics, there's a long way to go yet. However, no pain, no gain, so here goes.
Recall from the previous posts, that as the radius r, of the Bott expansion increases from 1 to 4, the magnitudes, defined mathematically by the dimensions and "directions" of the tetraktys, and geometrically by the LC, increase in two, reciprocal "directions," just as the number line of our familiar family of rational numbers does: 1/n, ...1/3, 1/2, 1/1, 2/1, 3/1, ...n/1. The difference is, of course, the Bott expansion is multi-dimensional.
The interesting discovery is that, taking the three-dimensional component of the expansions, enables us to draw a corollary between this series of expansions and the combinations of SUDRs and TUDRs (Ss and Ts), making up our new scalar motion equation, S|T (T|S) = 1/2 + 1/1 + 2/1 = 4|4, which is a scalar motion sum of the total cycles of the space and the time oscillations, for a given value of the Bott expansion radius, r. When we multiply this equation by r = 1 - 4, we get:
1(4|4) = 4|4;
2(4|4) = 8|8;
3(4|4) = 12|12;
4(4|4) = 16|16;
Remarkably, however, when we divide the corresponding number of the Bott LC expansion, 2n3, by these S|T and T|S numbers (the pipe symbol denotes the reciprocity of space and time oscillations), we get the number of elements in the corresponding sub-period of the periodic table:
8/4 = 2;
64/8 = 8;
216/12 = 18;
512/16 = 32;
Given that the RHS side of 4|4 is the reciprocal of the LHS, and the two LC expansions from the Bott expansion are also reciprocals, we seem justified in dividing the reciprocals as well. That is:
1/8 ÷ 1/4 = 1/2;
1/64 ÷ 1/8 = 1/8;
1/216 ÷ 1/12 = 1/18;
1/512 ÷ 1/16 = 1/32,
giving us the number of elements in the two sub-periods in each period of the periodic table, although in reciprocal form. Could it be that the fact that each 4n2 period consists of two 2n2 sub-periods, is due to one sub-period being the reciprocal of the other sub-period, just as in the Bott expansion and the scalar motion equation???
Though skeptical for weeks now, I decided to assume that the stack number (the number of cubes in a 2r3 stack of unit cubes), represents the limit of the number of r(4|4) units of natural scalar motion that can be accommodated for a given expansion of radius r. I really can't say that I understand a physical reason for this yet, but, intuitively, it seems likely. So, I went ahead and worked it out, as shown in the series of graphics below:

When r = 1, LC = 8, num = 4|4, resulting in two, reciprocal, sub-periods, with one element each: Hydrogen and Helium and one sub-element each.

When r = 2, LC = 64, num = 8|8, resulting in two, reciprocal, sub-periods, with eight elements each.

When r = 3, LC = 216, num = 12|12, resulting in two, reciprocal, sub-periods, with eighteen elements each.

When r = 4, LC = 512, num = 16|16, resulting in two, reciprocal, sub-periods, with thirty two elements each.
Now, this is an encouraging development, but, unfortunately, nature doesn't expand in cubes, and the scalar motion equation for the first atom, Hydrogen, has a total num of 108|108, and subsequent atoms are multiples of this value. However, since the equation for Hydrogen is 27/54+27/27+54/27 = 108|108, we can factor out this value to simplify to 27(1/2 + 1/1+2/1) = 27(4|4), although I don't show this factorization in the graphics above.
The most important implication of this result is that, if it proves valid, we now have a model of the atom for our RSt, which is based on the logical and mathematical progression of multi-dimensional numbers.
Re: Meeting a Terrific Challenge
What the Bott expansion makes clear is that the periodic table of elements, especially in its wheel of motion form, is not to be understood as built up atom by atom, proton by proton, as it were, but period by period. All the periods are three-dimensional; that is, the count proceeds 1, 2. 3, 4, but in three dimensions, which means the magnitude increases simultaneously in eight "directions," at each step:
13 x 23, 23 x 23, 33 x 23, 43 x 23,
or 8, 64, 216, 512,
and, as these are actually 3D sums, or numbers, each has its reciprocal:
(2n)3/(2n)3,
giving us a 3d number line, where 8 is now the unit number:
8/(2n)3, ...8/512, 8/216, 8/64, 8/8, 64/8, 216/8, 512/8, ...(2n)3/8
The periods result from the fact that the elements are combinations of space and time oscillations, which require a minimum of 4 units of space and 4 units of time for each cycle, which is expressed in the scalar motion equation:
n(S|T) = n(1/2 + 1/1 + 2/1) = n(4|4).
Thus, the periods of the wheel (table), consisting of two, reciprocal, sub-periods each, are derived as the quotient of the 3d stack numbers and the S|T numbers for a given value of n:
n = 1 --> 8|8 ÷ 4|4 = 2|2;
n = 2 --> 64|64 ÷ 8|8 = 8|8;
n = 3 --> 216|216 ÷ 12|12 = 18|18;
n = 4 --> 512|512 ÷ 16|16 = 32|32;
To apply this to the elements, however, we have to remember that we factored out the num of the Deuterium atom, which is not 4|4, but 108|108. The scalar motion equation for the Deuterium atom is:
27(S|T) = 27(1/2 + 1/1 + 2/1) = (27/54 + 27/27 + 54/27) = 108|108,
and therefore the corresponding stack number is 543 = 157464, which is 273 times the eight "directions" of the unit stack, or 273 x 23. Hence, we have to multiply both sides of the periodic equations by this number:
273(8|8)÷273(4|4) = 2|2, giving us:
n = 1 --> 273(8|8 ÷ 4|4) = 273(2|2);
n = 2 --> 273(64|64 ÷ 8|8) = 273(8|8);
n = 3 --> 273(216|216 ÷ 12|12) = 273(18|18);
n = 4 --> 273(512|512 ÷ 16|16) = 273(32|32);
for the four periods of the wheel (table).
This is a welcome insight, for sure, but nature does not expand by the numbers. As the science of geometry proves, there are as many distinct geometric directions defined by lines drawn between the center point of a circle and points on its circumference, as there are points on the circumference, which are infinitely many. However, if we choose a set of points on a circumference of a circle of radius r, then we know that it will be a subset of a set of equal magnitudes on the circumference of a circle of radius r + 1.
In our special case, the smallest subset is equal to 2, when r=1, and the set corresponding to r=2, is 8, or r2 times larger, and the difference between them is 8-2=6. The set when r=3 is 18, or r2 times larger than the r=1 subset, and the difference between it and the previous set is 18-8=10. Finally, when r=4, the set is 32, or r2 times larger than the r=1 subset, and the difference between it and the previous set is 32-18=14.
Of course, these differences, 2, 6, 10 and 14, are identical to the numbers of the spectral energy groups, s, p, d and f that are so fundamental to the science of spectroscopy and quantum mechanics, and, when combined with the absolute value of their reciprocals, we get the match between the 2s, 2p, 2d and 2f of the spectral groups and the 4n2 periods of the table (wheel).
However, since the cubic expansion of the tetraktys, the LC, and the Bott expansion defines the three continuous magnitudes of the 1d, 2d and 3d balls of the LC, with radius √1, √2, √3, respectively, we recognize that these three magnitudes are the "real" magnitudes of nature's universal expansion of space and time, as posited by the RST.
Consequently, we need to add these magnitudes, as r√1, r√2 and r√3, to our Bott expansion graphic:

Consequently, with each step of the (factored) Bott expansion (n = 1 - 4), the volume of the three balls defined by the expanding LC also increases, each according to its expanding radius. For the 3d radius, √3, the expansion is:
n = 1 --> √3;
n = 2 --> √12;
n = 3 --> √27;
n = 4 --> √48;
However, unlike the cubic magnitudes of the stack numbers, the magnitudes of the volumes associated with these radii are not integer values. They are irrational numbers, so dividing them by the corresponding n(S|T) num values of the scalar motion equation, as we did in the case of the integer stack numbers, will not work.
Nevertheless, what we can do is recognize that each cycle of the oscillations is equivalent to a 4π rotation, as we've shown previously (see the Introduction thread of this topic.) If we proceed on this basis, calculating the volume of the 3d ball for a given radius and dividing it by 4π, or
V ÷ n(4π) = ((4/3)π x r3) ÷ n(4π),
we get:
n =1 ---> √3:
n =2 ---> √48:
n =3 ---> √243:
n =4 ---> √768:
The result is that this procedure gives us a series of continuous magnitudes (and its inverse), which corresponds to the series of discrete magnitudes (and its inverse) that constitute the (factored) sub-periods of the wheel (table), as shown in the previous posts above. In other words, as the (factored) Bott expansion expands, the inverse LCs expand and the volumes associated with them expand as well, As the (factored) LCs expand, the (factored) number of discrete natural units of scalar motion increases up to the discrete limit of that (factored) volume, and as the (factored) number of continuous volume increases, the continuous number of (factored) 4π cycles increases up to the limit of that (factored) continuous volume.
This means we can add the continuous numbers to the discrete numbers in the two sub-periods of each period of the wheel (table). However, to make it cleaner and simpler to illustrate, the notation used requires some explanation: As it turns out, the volume per 4π cycle in a given sub-period increases quadratically with each increment of n (the factorization is to be understood from this point on):
√3 ÷ √3 = 1 or 12
√48 ÷ √3 = 4 or 22
√243 ÷ √3 = 9 or 32
√768 ÷ √3 = 16 or 42,
that is to say, it increases by n2. Therefore, if we know the unit volume per cycle for a given period, we can simply multiply this unit value by the square of the slot number for the element in the sub-period, to get the appropriate value of a given element in a given sub-period. Accordingly, I have modified the previous series of images for the four periods of the wheel to include these continuous values, as shown below:




So, to calculate the continuous number for a given element in a given sub-period, we simply multiply the unit volume (√1, √48, √243, √768), for that period (located at the bottom of the inner circle), by the squared slot number indicated for that element's position in the appropriate sub-period.
The result is a continuous number for each element that corresponds to the discrete natural units of motion (num) number for each element. With these continuous magnitudes in hand, it should be possible to ascertain the physical and chemical properties of the elements. We'll see.
13 x 23, 23 x 23, 33 x 23, 43 x 23,
or 8, 64, 216, 512,
and, as these are actually 3D sums, or numbers, each has its reciprocal:
(2n)3/(2n)3,
giving us a 3d number line, where 8 is now the unit number:
8/(2n)3, ...8/512, 8/216, 8/64, 8/8, 64/8, 216/8, 512/8, ...(2n)3/8
The periods result from the fact that the elements are combinations of space and time oscillations, which require a minimum of 4 units of space and 4 units of time for each cycle, which is expressed in the scalar motion equation:
n(S|T) = n(1/2 + 1/1 + 2/1) = n(4|4).
Thus, the periods of the wheel (table), consisting of two, reciprocal, sub-periods each, are derived as the quotient of the 3d stack numbers and the S|T numbers for a given value of n:
n = 1 --> 8|8 ÷ 4|4 = 2|2;
n = 2 --> 64|64 ÷ 8|8 = 8|8;
n = 3 --> 216|216 ÷ 12|12 = 18|18;
n = 4 --> 512|512 ÷ 16|16 = 32|32;
To apply this to the elements, however, we have to remember that we factored out the num of the Deuterium atom, which is not 4|4, but 108|108. The scalar motion equation for the Deuterium atom is:
27(S|T) = 27(1/2 + 1/1 + 2/1) = (27/54 + 27/27 + 54/27) = 108|108,
and therefore the corresponding stack number is 543 = 157464, which is 273 times the eight "directions" of the unit stack, or 273 x 23. Hence, we have to multiply both sides of the periodic equations by this number:
273(8|8)÷273(4|4) = 2|2, giving us:
n = 1 --> 273(8|8 ÷ 4|4) = 273(2|2);
n = 2 --> 273(64|64 ÷ 8|8) = 273(8|8);
n = 3 --> 273(216|216 ÷ 12|12) = 273(18|18);
n = 4 --> 273(512|512 ÷ 16|16) = 273(32|32);
for the four periods of the wheel (table).
This is a welcome insight, for sure, but nature does not expand by the numbers. As the science of geometry proves, there are as many distinct geometric directions defined by lines drawn between the center point of a circle and points on its circumference, as there are points on the circumference, which are infinitely many. However, if we choose a set of points on a circumference of a circle of radius r, then we know that it will be a subset of a set of equal magnitudes on the circumference of a circle of radius r + 1.
In our special case, the smallest subset is equal to 2, when r=1, and the set corresponding to r=2, is 8, or r2 times larger, and the difference between them is 8-2=6. The set when r=3 is 18, or r2 times larger than the r=1 subset, and the difference between it and the previous set is 18-8=10. Finally, when r=4, the set is 32, or r2 times larger than the r=1 subset, and the difference between it and the previous set is 32-18=14.
Of course, these differences, 2, 6, 10 and 14, are identical to the numbers of the spectral energy groups, s, p, d and f that are so fundamental to the science of spectroscopy and quantum mechanics, and, when combined with the absolute value of their reciprocals, we get the match between the 2s, 2p, 2d and 2f of the spectral groups and the 4n2 periods of the table (wheel).
However, since the cubic expansion of the tetraktys, the LC, and the Bott expansion defines the three continuous magnitudes of the 1d, 2d and 3d balls of the LC, with radius √1, √2, √3, respectively, we recognize that these three magnitudes are the "real" magnitudes of nature's universal expansion of space and time, as posited by the RST.
Consequently, we need to add these magnitudes, as r√1, r√2 and r√3, to our Bott expansion graphic:

Consequently, with each step of the (factored) Bott expansion (n = 1 - 4), the volume of the three balls defined by the expanding LC also increases, each according to its expanding radius. For the 3d radius, √3, the expansion is:
n = 1 --> √3;
n = 2 --> √12;
n = 3 --> √27;
n = 4 --> √48;
However, unlike the cubic magnitudes of the stack numbers, the magnitudes of the volumes associated with these radii are not integer values. They are irrational numbers, so dividing them by the corresponding n(S|T) num values of the scalar motion equation, as we did in the case of the integer stack numbers, will not work.
Nevertheless, what we can do is recognize that each cycle of the oscillations is equivalent to a 4π rotation, as we've shown previously (see the Introduction thread of this topic.) If we proceed on this basis, calculating the volume of the 3d ball for a given radius and dividing it by 4π, or
V ÷ n(4π) = ((4/3)π x r3) ÷ n(4π),
we get:
n =1 ---> √3:
n =2 ---> √48:
n =3 ---> √243:
n =4 ---> √768:
The result is that this procedure gives us a series of continuous magnitudes (and its inverse), which corresponds to the series of discrete magnitudes (and its inverse) that constitute the (factored) sub-periods of the wheel (table), as shown in the previous posts above. In other words, as the (factored) Bott expansion expands, the inverse LCs expand and the volumes associated with them expand as well, As the (factored) LCs expand, the (factored) number of discrete natural units of scalar motion increases up to the discrete limit of that (factored) volume, and as the (factored) number of continuous volume increases, the continuous number of (factored) 4π cycles increases up to the limit of that (factored) continuous volume.
This means we can add the continuous numbers to the discrete numbers in the two sub-periods of each period of the wheel (table). However, to make it cleaner and simpler to illustrate, the notation used requires some explanation: As it turns out, the volume per 4π cycle in a given sub-period increases quadratically with each increment of n (the factorization is to be understood from this point on):
√3 ÷ √3 = 1 or 12
√48 ÷ √3 = 4 or 22
√243 ÷ √3 = 9 or 32
√768 ÷ √3 = 16 or 42,
that is to say, it increases by n2. Therefore, if we know the unit volume per cycle for a given period, we can simply multiply this unit value by the square of the slot number for the element in the sub-period, to get the appropriate value of a given element in a given sub-period. Accordingly, I have modified the previous series of images for the four periods of the wheel to include these continuous values, as shown below:




So, to calculate the continuous number for a given element in a given sub-period, we simply multiply the unit volume (√1, √48, √243, √768), for that period (located at the bottom of the inner circle), by the squared slot number indicated for that element's position in the appropriate sub-period.
The result is a continuous number for each element that corresponds to the discrete natural units of motion (num) number for each element. With these continuous magnitudes in hand, it should be possible to ascertain the physical and chemical properties of the elements. We'll see.
Re: Meeting a Terrific Challenge
There are no Green Vertical arrows on this diagram.
There are no Green Horizontal arrows on this diagram.
I'll wait until you update it and make an accurate Legend for it.dbundy wrote: ↑Sun Oct 28, 2018 4:22 pm Now, after I posted the graphic for the two world line charts, I realized that it was outdated. When I first conceived of it, I wasn't thinking in terms of rotating the entire chart to obtain the reciprocal world line, but only the unit progression arrows. This generated an incorrect reciprocal progression, where the "direction" of reciprocal space progression is directly opposite the "direction" of the space progression, and the same for time.
However, when the entire chart is rotated to plot the reciprocal, the "direction" of the vertical time progression rotates to oppose the "direction" of the horizontal space progression, and the "direction" of the horizontal space progression rotates to oppose the "direction" of the time progression in the vertical. I intend to update the graphic as soon as I can.
Re: Meeting a Terrific Challenge
Horace, didn't I post this corrected graphic already?
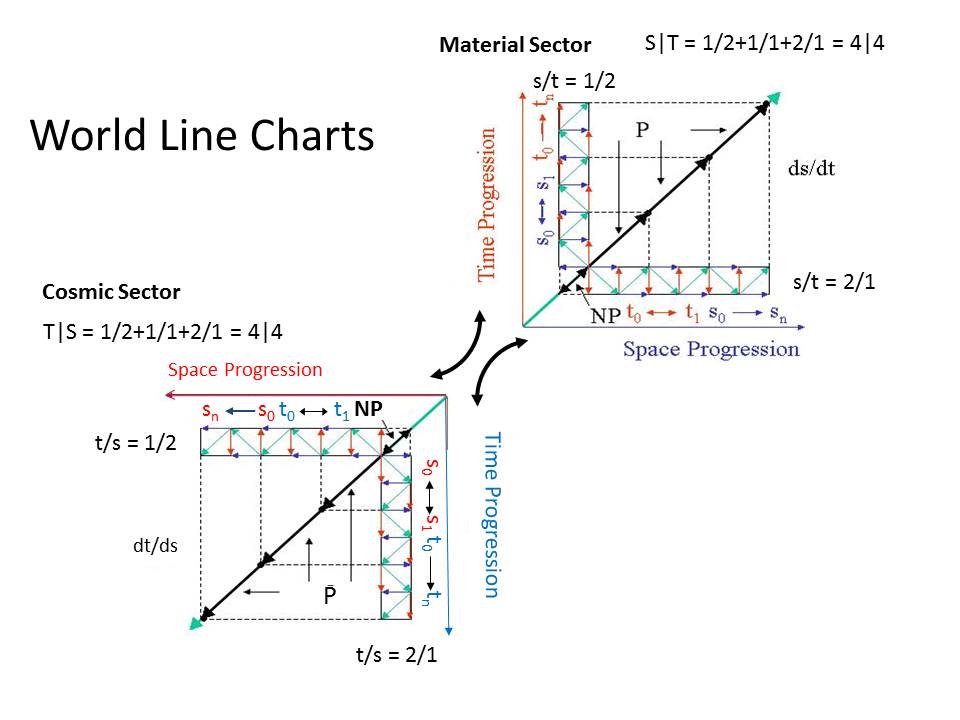
The green, zig-zaging, arrows are increasing vertically upwards, and the green, zig-zagging, arrows are increasing horizontally to the right in the MS, and vertically downwards and horizontally to the left in the CS. These are representations of space and time oscillations.

The green, zig-zaging, arrows are increasing vertically upwards, and the green, zig-zagging, arrows are increasing horizontally to the right in the MS, and vertically downwards and horizontally to the left in the CS. These are representations of space and time oscillations.
Re: Meeting a Terrific Challenge
The Wheel of Motion form of the Periodic Table of Elements is helpful in that it is more compact and shows why there are gaps and longer and longer rows in the table. However, now that we have discovered that the two sub-periods of each period are actually reciprocals, it may be easier to illustrate the reciprocal aspect in the table format, because we are accustomed to writing the rational number line, as a horizontal reflection symmetry: 1/n, ...1/3, 1/2, 1/1, 2/1, 3/1, ...n/1.
In fact, we've already done that, when we were trying to map the electron configuration to the tetraktys. The reciprocal aspect in that case is quite evident, but it seems the same format might be used for the table of elements. Actually, when we consider the LST's mapping of the electron configuration, we find that the reciprocal aspect is incorporated in it too, something I didn't realize before:
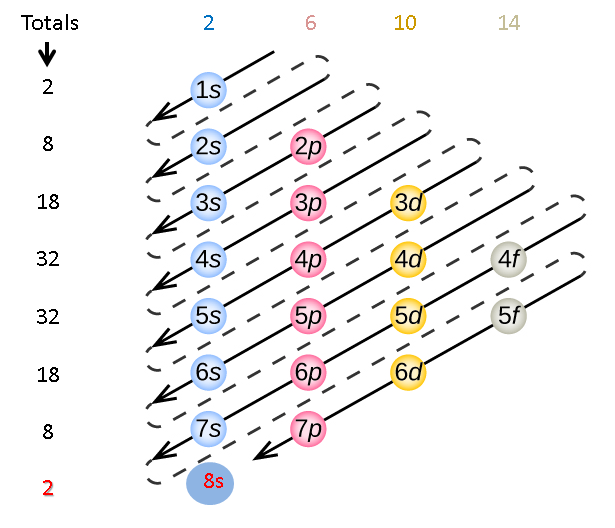
I had to add the 8s group to the image above to complete it, but the reciprocity is clear, even though the filling pattern, as we know from the Le Cornec ionization data, is probably incorrect in terms of the order of the spectral groups. Clearly, in terms of the order of the sub-periods, though, which are the totals of the horizontal rows of spectral groups, the pattern is reciprocal:
2, 8, 18, 32....32, 18, 8, 2
I find it very interesting, since I doubt very much that this was anything but innocent, since, as far as I know, no one has ever pointed it out before, even though it's very obvious. The question is, why does this reciprocity appear in the mapping? Is there an identifiable connection to the reciprocal sub-periods in our work?
Actually, as crazy as it might seem, there is. If we split the image horizontally and swing the bottom half up to meet the top half, we get the spectral tetraktys, hiding in plain sight!
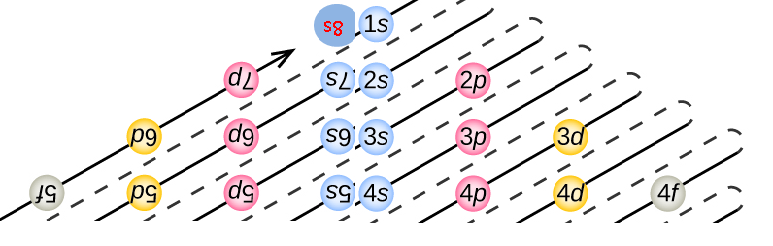
I don't know what to make of it, really, but could it be just another coincidence?
In fact, we've already done that, when we were trying to map the electron configuration to the tetraktys. The reciprocal aspect in that case is quite evident, but it seems the same format might be used for the table of elements. Actually, when we consider the LST's mapping of the electron configuration, we find that the reciprocal aspect is incorporated in it too, something I didn't realize before:

I had to add the 8s group to the image above to complete it, but the reciprocity is clear, even though the filling pattern, as we know from the Le Cornec ionization data, is probably incorrect in terms of the order of the spectral groups. Clearly, in terms of the order of the sub-periods, though, which are the totals of the horizontal rows of spectral groups, the pattern is reciprocal:
2, 8, 18, 32....32, 18, 8, 2
I find it very interesting, since I doubt very much that this was anything but innocent, since, as far as I know, no one has ever pointed it out before, even though it's very obvious. The question is, why does this reciprocity appear in the mapping? Is there an identifiable connection to the reciprocal sub-periods in our work?
Actually, as crazy as it might seem, there is. If we split the image horizontally and swing the bottom half up to meet the top half, we get the spectral tetraktys, hiding in plain sight!

I don't know what to make of it, really, but could it be just another coincidence?
Re: Meeting a Terrific Challenge
Since this is the International Year of the Periodic Table, it would be wonderful, if we could host a major event to celebrate our discoveries of the true nature of the Periodic Law on which all of the profoundness is based.
Alas, however, it's inconceivable that such an event would be able to garner any attention from the scientific community, let alone the general public, because no one, outside of our minuscule society, is prepared to understand our new atomic model, since it is based on scalar motion, which no one else understands or accepts. And since the new scalar motion model is not Larson's model, but the LRC's model, it's even more difficult to make a convincing case for it.
In 1998, I used Larson's scalar motion atomic model to show how the 4n2 periods of the periodic table could be drawn as concentric circles, not realizing then that the reciprocity of the circles represented the reciprocity of the sub-periods.
It wasn't until this year, using our new scalar motion model of the atom, that the reciprocity of the sub-periods, in the concentric circles, clearly emerged, after discovering it in the form of the Bott expansion, but how can this be taught to the uninitiated? Where do we begin? After all these years, we can't even get Dewey Larson's revolutionary new program of physical research a mention in Wikipedia, let alone an exposition.
I don't know what the answer is, but I, for one, can never go back to a world where scalar motion is not even recognized as a legitimate form of motion. In all the talk of the table's profoundness, at the big kickoff event in Paris, no mention is made of dimensions, of the tetraktys, or why the periods are what they are. Mendeleev thought that the fundamental period of the table was 8, but when the larger periods were discovered, his idea was discarded. How ironic this appears now that we can see that the number 8 (twice four), of Bott periodicity, does indeed play a fundamental role in the periods of the table.
But it's not numerology that we are dealing with here, as some, like Randell Mills, would like to think. No, it's the fundamental structure of the universe we see emerging, when the scalar motion of the universe is properly understood. Look at the spectral tetraktys. It is really composed of two, reciprocal tetraktii, if you will, which we can see in the LST's mnemonic for establishing the electron configuration of an atom, which was shown in the previous post. Just take the binomial expansion form of the tetraktys, and write its numbers as columns and rows, instead of a triangle, and write its reciprocal as a reflection of it and you get the spectral tetraktys, populated with the "directions" of its respective dimensions.
And since the tetraktys is the dimensional map of the LC's geometry, the spectral tetraktys is the dimensional map of the S|T combination, formulated as the natural motion equation, all of which are expressions of the same reciprocity - a unification of numbers, geometry and physics:
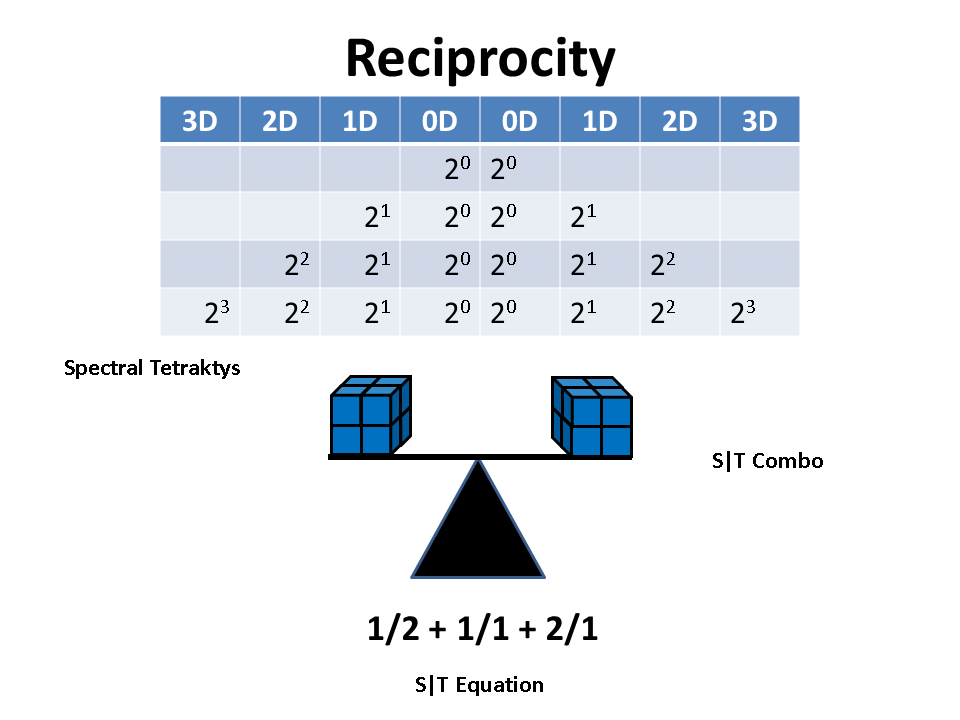
But what about the periodic table? The chemical ordering of the elements does not show the same form of reciprocal magnitudes, dimensions and "directions," as shown in the above graphic. This is true, but it was ordered in terms of groups of certain similarities in the properties of the elements. However, the periods of the table do follow the "Periodic Law," which, as we have seen in previous posts, is generated by the Bott expansion.
In fact, a popular physicist version of the table, Stowe's Periodic Table, has the same dimensional form as the LST's mnemonic for Electron Configuration:
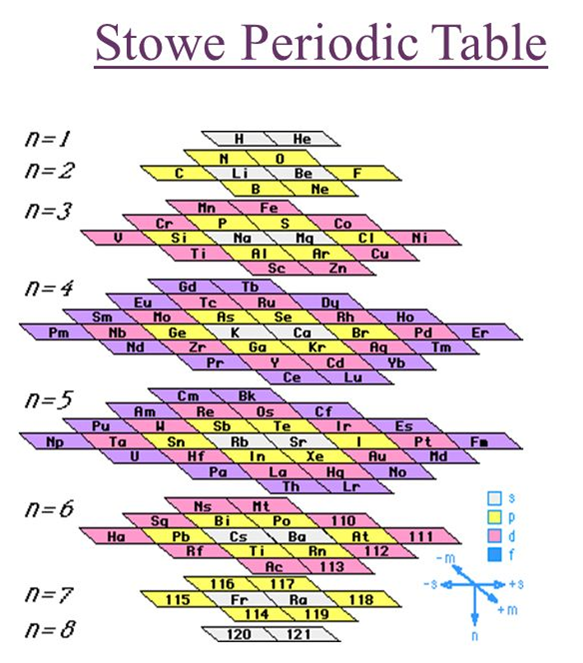
The physicists love the symmetry of the table, which they see as a "bilateral" symmetry, and it leaves room for new elements, which we maintain do not exist, by virtue of the proven Bott periodicity theorem, which proves that there are no physical phenomena beyond three (four counting 0) dimensions.
Thus, the value of n, as shown in the graphic above, cannot go beyond 4, the maximum number of dimensions, which means we simply need to slice the graphic in two horizontally and rotate the bottom half up to be opposite the top half, as its reciprocal, just as we did with the Electron Configuration mnemonic, and voila, the periodic table takes the same form as the spectral tetraktys!
This at once clarifies that the periods of the table are 4n2 and eliminates the possibility for elements beyond 118.
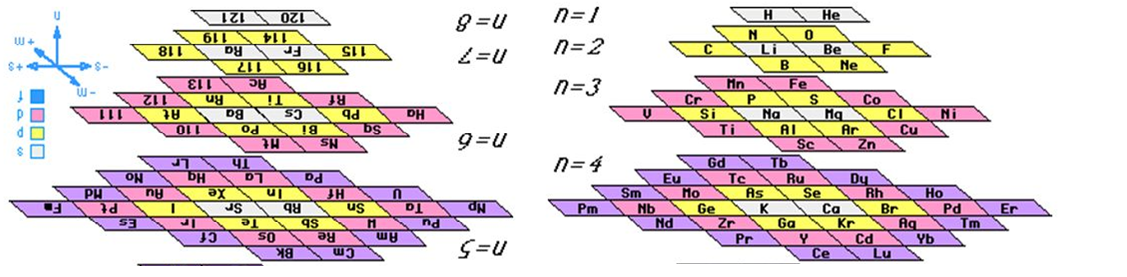
Imagine explaining this to the crowd in Paris. Heck, I would be happy to explain it to the crowd in Salt Lake City!
Alas, however, it's inconceivable that such an event would be able to garner any attention from the scientific community, let alone the general public, because no one, outside of our minuscule society, is prepared to understand our new atomic model, since it is based on scalar motion, which no one else understands or accepts. And since the new scalar motion model is not Larson's model, but the LRC's model, it's even more difficult to make a convincing case for it.
In 1998, I used Larson's scalar motion atomic model to show how the 4n2 periods of the periodic table could be drawn as concentric circles, not realizing then that the reciprocity of the circles represented the reciprocity of the sub-periods.
It wasn't until this year, using our new scalar motion model of the atom, that the reciprocity of the sub-periods, in the concentric circles, clearly emerged, after discovering it in the form of the Bott expansion, but how can this be taught to the uninitiated? Where do we begin? After all these years, we can't even get Dewey Larson's revolutionary new program of physical research a mention in Wikipedia, let alone an exposition.
I don't know what the answer is, but I, for one, can never go back to a world where scalar motion is not even recognized as a legitimate form of motion. In all the talk of the table's profoundness, at the big kickoff event in Paris, no mention is made of dimensions, of the tetraktys, or why the periods are what they are. Mendeleev thought that the fundamental period of the table was 8, but when the larger periods were discovered, his idea was discarded. How ironic this appears now that we can see that the number 8 (twice four), of Bott periodicity, does indeed play a fundamental role in the periods of the table.
But it's not numerology that we are dealing with here, as some, like Randell Mills, would like to think. No, it's the fundamental structure of the universe we see emerging, when the scalar motion of the universe is properly understood. Look at the spectral tetraktys. It is really composed of two, reciprocal tetraktii, if you will, which we can see in the LST's mnemonic for establishing the electron configuration of an atom, which was shown in the previous post. Just take the binomial expansion form of the tetraktys, and write its numbers as columns and rows, instead of a triangle, and write its reciprocal as a reflection of it and you get the spectral tetraktys, populated with the "directions" of its respective dimensions.
And since the tetraktys is the dimensional map of the LC's geometry, the spectral tetraktys is the dimensional map of the S|T combination, formulated as the natural motion equation, all of which are expressions of the same reciprocity - a unification of numbers, geometry and physics:

But what about the periodic table? The chemical ordering of the elements does not show the same form of reciprocal magnitudes, dimensions and "directions," as shown in the above graphic. This is true, but it was ordered in terms of groups of certain similarities in the properties of the elements. However, the periods of the table do follow the "Periodic Law," which, as we have seen in previous posts, is generated by the Bott expansion.
In fact, a popular physicist version of the table, Stowe's Periodic Table, has the same dimensional form as the LST's mnemonic for Electron Configuration:

The physicists love the symmetry of the table, which they see as a "bilateral" symmetry, and it leaves room for new elements, which we maintain do not exist, by virtue of the proven Bott periodicity theorem, which proves that there are no physical phenomena beyond three (four counting 0) dimensions.
Thus, the value of n, as shown in the graphic above, cannot go beyond 4, the maximum number of dimensions, which means we simply need to slice the graphic in two horizontally and rotate the bottom half up to be opposite the top half, as its reciprocal, just as we did with the Electron Configuration mnemonic, and voila, the periodic table takes the same form as the spectral tetraktys!
This at once clarifies that the periods of the table are 4n2 and eliminates the possibility for elements beyond 118.

Imagine explaining this to the crowd in Paris. Heck, I would be happy to explain it to the crowd in Salt Lake City!
Re: Meeting a Terrific Challenge
Once again, we've developed some pretty exciting results by employing Dewey Larson's RST. However, making it easily understandable will not be a simple task. Indeed, it's entirely possible that something has been confused or overlooked that's going to leave me with egg on my face in the end.
Nevertheless, the truth is I've tried my best to stick to mathematical, geometric and logical principles from beginning to end, and it appears that a new, scalar-motion model of the atom has now emerged that can account for the spectral and periodic characteristics of the set of 118 observed chemical elements (or the sum of observed and synthesized elements).
This is truly a major scientific breakthrough, underscored by the presentations at UNESCO's kickoff event of the IYPT last month at its headquarters in Paris. The website explains:
I am attempting to find an appropriate notation that, once understood, will convey the fundamental nature of this new approach. It's not easy. In fact, the notation used in the graphics of the previous posts above need to be corrected and revised. However, no matter how good the notation, it will still be difficult to convey its meaning, without substantial exposition. For instance, how does a linearly increasing number of elements consist of two reciprocal sub-sets?
As can be seen from the quantum number-based Stowe Periodic Table, which we modified in the previous post above, the structure of the spectral tetraktys in the table is clear, once the four dimensional limit of the Bott periodicity theorem is applied. At each dimension, there are two, reciprocal, sets of "s shells." These two sets are the only ones, at the 0 dimensional level. At the 1 dimensional level, two sets of reciprocal "p shells" are added. In the 3rd dimension, these are joined by two sets of "d shells," and, finally, in the 4th dimension, two "f shells" are added, for a total of (2|2)+(2+6)|(2+6)+(2+6+10)|(2+6+10)+(2+6+10+14)|(2+6+10+14) = 2|2+8|8+18|18+32|32 = 60|60 (but only two of the four 0 dimensional slots are counted as elements, so 118 all together).
As also shown in the previous post above, the "s shells" are 0 dimensional; the "p shells" are 1 dimensional; the "d shells" are 2 dimensional, and the "f shells" are 3 dimensional, and by the Bott periodicity theorem, we know that there can be no new phenomena beyond these dimensions, because they just repeat, like a set of Russian dolls that fit one inside the other.
In other words, as the dimensions increase, from 0 to 3, the combination of protons increases its degree of freedom, as explained previously. This clearly follows the LST's quantum numbers, as shown in the graphic below, revealing the reciprocal and dimensional character of their approach:

The Periodic Law stems from two, reciprocal, tetraktii, populated with the atomic spectral groups, according to the degree of freedom specified by four quantum numbers, n, l, m and s (s, for spin, is not explicitly labeled in the graphic, but indicated as the (+/-) sign of the spectral groups in the first, or top row of the table.)
The increase in the degree of freedom, as the dimension increases, is shown graphically in the modified Stowe table, as concentric circles of rectangles, the number and radii of which increases as the dimension increases. The correspondence of these characteristics with the values of the quantum number m, including the reciprocity, is unmistakable.
So, how do we diagram the increasing atomic number over two, reciprocal sets in each dimension? As it happens, this is probably not practical (or even possible?) in the table format, since its linear order conflicts with the changing "direction" of the circle's reciprocity, which loops back on itself. It seems we can illustrate one or the other but not both, in the table format. For instance, the Janet table, the so-called left-step table, shows the correct reading order of the elements, from left-to-right, top-to-bottom, but not the reciprocity, as we saw in our modified Stowe table (see previous post). Yet, while the modified Stowe table shows the reciprocity, the order of the elements is hardly straightforward.
Only in our Wheel of Motion format of concentric circles are we able to capture both the order of the elements AND their reciprocity, at least as far as I can determine. This is true because the clockwise ordering of the elements in each period continuously increases, even though the vertical "direction" of the sub-period order reverses 180 degrees at the six o'clock position, from a descending "direction" to an ascending "direction," we might say, and then repeats, or cycles.
This change of "direction" is well-known in LST physics and mathematics and is used to graph the positive and negative "directions" of electronic signals. In the case of the Wheel of Motion, the position of each "positive" element has a reciprocal position for a "negative" element, within a given period, as shown in the graphic below, color coded to match the table in the graphic above:
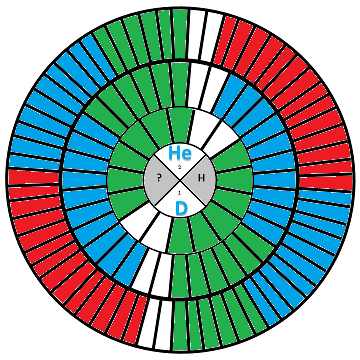
Four concentric circles, containing 4, 16, 36, and 64 "slots," one for each element of the periodic table, captures both the linear characteristic of the atomic numbers of the four periods and the reciprocity characteristic of the eight sub-periods.
However, as with the standard periodic table, the order of the spectral groups (s, p, d and f) in these circles does not follow the order in the previous graphic, because, again, the linearity of the order sequence forces the s groups out of their proper place and into the next group's sequence. The patterns of the modified Stowe table solves this somewhat, by placing the s group at the center of each of a set of concentric circles. Borrowing this format, we can modify the above graphic accordingly.
First, following the same spectral group color scheme, as in the above graphics, we can convert the reciprocal tetraktys pattern using circles, labeling them with their respective number of slots, and changing their relative sizes:
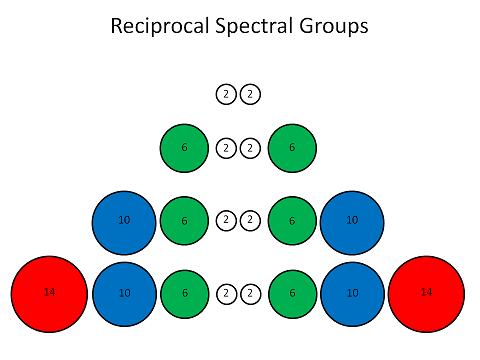
This places the groups in the proper "tetraktys" order, going from smallest to largest, in two reciprocal "directions," as the dimension increases from 0, at the top, to 3, at the bottom, which works, except, when we number the elements. When we number them, element number 21,Sc, is the first element in the (blue) d group, instead of the first element in the (green) p group, as previously was the case. This is the vexing problem. How is it that the larger d group intercedes between the s and p groups like this? And the same thing happens at the next level; The first element at this level is the first element in the (red) f group, element number 57, La, not the first element in the (green) p group!
We can combine these groups, following the Stowe table format, placing the small s group in the middle of the larger groups:
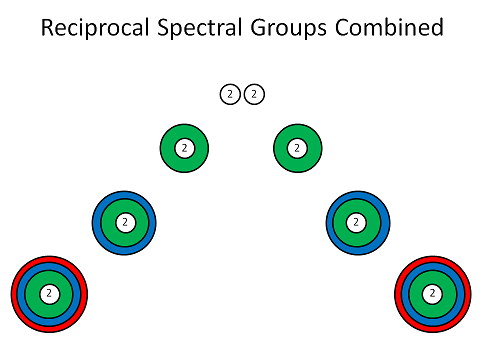
This is good, but numbering the elements still requires us to jump from the center s group of a given set to the outer group of that set and work our way back to the center. This is so odd and just plain inexplicable!!!
In grappling with this, I came across Eric Scerri's articles and Youtube discussions on the periodic table, and he referred to the late Fernando Dufour, as the foremost researcher of the table, who designed a 3d model of it.
When I checked it out, I discovered that Dufour went beyond Stowe's design in that he removed the s groups from the linear succession, which is making it so difficult to understand how to format the table, consistent with all the constraints, and he placed them in their own dimension, the third dimension (the third dimension of space, not the tetraktys).
Wow, this does the trick, as shown in the next graphic, where I combined Stowe's and Dufour's ideas with my own:
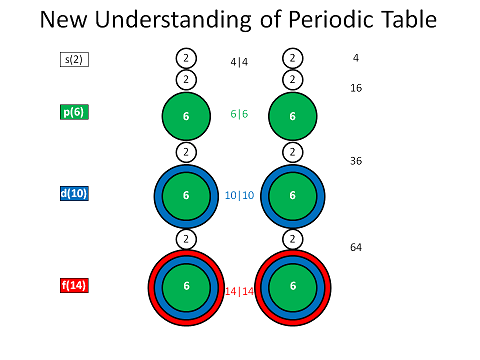
In this new, abstract, version of the scalar-motion based Periodic Schematic of the Elements, the s group elements are treated as transition elements, which connect the four dimensions of the Reciprocal Tetraktys.
The new schematic shows how the Bott periodicity (modulo 8) plays between the four dimensions, producing the interval 8 between the reciprocal sub-periods of the elements: 4 + 8 = 6+6 = 12; 12 + 8 = 10+10 = 20; 20 + 8 = 14+14 = 28 (or s|s; p|p; d|d; f|f). When the 2+6 (s+p) fundamental is added to each dimension's increased degree of freedom, the sub-periods are produced (8 + 0 = 8; 8 + 10 = 18; 8 + 24 = 32).
The abstraction hides the many details that are only implied, but, taking the s groups out of the linear sequence of elements, allows us to see that they are common to all the groups of a set. In the first instance, the transition from 0 to 1 dimension, the two p groups appear to be uniquely associated with the two s groups, but this is an illusion due to the fact that the p groups are the only members of that set. When the schematic transitions to dimension 2, the d group encircles the p group, and upon transitioning to dimension 3, the f group encircles both the d and p groups.
The rule is that the atomic number sequence always begins with the outermost group, through the s group, which is now understandable, given the schematic, even if it's not entirely clear how this is to be interpreted physically, yet.
Stay tuned!
Nevertheless, the truth is I've tried my best to stick to mathematical, geometric and logical principles from beginning to end, and it appears that a new, scalar-motion model of the atom has now emerged that can account for the spectral and periodic characteristics of the set of 118 observed chemical elements (or the sum of observed and synthesized elements).
This is truly a major scientific breakthrough, underscored by the presentations at UNESCO's kickoff event of the IYPT last month at its headquarters in Paris. The website explains:
How fitting, then, that we can now offer the world a scalar-motion based version of the table that reveals, for the first time, why the periods of the table are what they are, and how they actually consists of two, reciprocal, sub-periods, even though the set of elements consists of a successive increase of atomic number, from 1 to 118.The Periodic Table of Chemical Elements is one of the most significant achievements in science, capturing the essence not only of chemistry, but also of physics and biology.
1869 is considered as the year of discovery of the Periodic System by Dmitri Mendeleev. 2019 will be the 150th anniversary of the Periodic Table of Chemical Elements and has therefore been proclaimed the "International Year of the Periodic Table of Chemical Elements (IYPT2019)" by the United Nations General Assembly and UNESCO.
I am attempting to find an appropriate notation that, once understood, will convey the fundamental nature of this new approach. It's not easy. In fact, the notation used in the graphics of the previous posts above need to be corrected and revised. However, no matter how good the notation, it will still be difficult to convey its meaning, without substantial exposition. For instance, how does a linearly increasing number of elements consist of two reciprocal sub-sets?
As can be seen from the quantum number-based Stowe Periodic Table, which we modified in the previous post above, the structure of the spectral tetraktys in the table is clear, once the four dimensional limit of the Bott periodicity theorem is applied. At each dimension, there are two, reciprocal, sets of "s shells." These two sets are the only ones, at the 0 dimensional level. At the 1 dimensional level, two sets of reciprocal "p shells" are added. In the 3rd dimension, these are joined by two sets of "d shells," and, finally, in the 4th dimension, two "f shells" are added, for a total of (2|2)+(2+6)|(2+6)+(2+6+10)|(2+6+10)+(2+6+10+14)|(2+6+10+14) = 2|2+8|8+18|18+32|32 = 60|60 (but only two of the four 0 dimensional slots are counted as elements, so 118 all together).
As also shown in the previous post above, the "s shells" are 0 dimensional; the "p shells" are 1 dimensional; the "d shells" are 2 dimensional, and the "f shells" are 3 dimensional, and by the Bott periodicity theorem, we know that there can be no new phenomena beyond these dimensions, because they just repeat, like a set of Russian dolls that fit one inside the other.
In other words, as the dimensions increase, from 0 to 3, the combination of protons increases its degree of freedom, as explained previously. This clearly follows the LST's quantum numbers, as shown in the graphic below, revealing the reciprocal and dimensional character of their approach:

The Periodic Law stems from two, reciprocal, tetraktii, populated with the atomic spectral groups, according to the degree of freedom specified by four quantum numbers, n, l, m and s (s, for spin, is not explicitly labeled in the graphic, but indicated as the (+/-) sign of the spectral groups in the first, or top row of the table.)
The increase in the degree of freedom, as the dimension increases, is shown graphically in the modified Stowe table, as concentric circles of rectangles, the number and radii of which increases as the dimension increases. The correspondence of these characteristics with the values of the quantum number m, including the reciprocity, is unmistakable.
So, how do we diagram the increasing atomic number over two, reciprocal sets in each dimension? As it happens, this is probably not practical (or even possible?) in the table format, since its linear order conflicts with the changing "direction" of the circle's reciprocity, which loops back on itself. It seems we can illustrate one or the other but not both, in the table format. For instance, the Janet table, the so-called left-step table, shows the correct reading order of the elements, from left-to-right, top-to-bottom, but not the reciprocity, as we saw in our modified Stowe table (see previous post). Yet, while the modified Stowe table shows the reciprocity, the order of the elements is hardly straightforward.
Only in our Wheel of Motion format of concentric circles are we able to capture both the order of the elements AND their reciprocity, at least as far as I can determine. This is true because the clockwise ordering of the elements in each period continuously increases, even though the vertical "direction" of the sub-period order reverses 180 degrees at the six o'clock position, from a descending "direction" to an ascending "direction," we might say, and then repeats, or cycles.
This change of "direction" is well-known in LST physics and mathematics and is used to graph the positive and negative "directions" of electronic signals. In the case of the Wheel of Motion, the position of each "positive" element has a reciprocal position for a "negative" element, within a given period, as shown in the graphic below, color coded to match the table in the graphic above:

Four concentric circles, containing 4, 16, 36, and 64 "slots," one for each element of the periodic table, captures both the linear characteristic of the atomic numbers of the four periods and the reciprocity characteristic of the eight sub-periods.
However, as with the standard periodic table, the order of the spectral groups (s, p, d and f) in these circles does not follow the order in the previous graphic, because, again, the linearity of the order sequence forces the s groups out of their proper place and into the next group's sequence. The patterns of the modified Stowe table solves this somewhat, by placing the s group at the center of each of a set of concentric circles. Borrowing this format, we can modify the above graphic accordingly.
First, following the same spectral group color scheme, as in the above graphics, we can convert the reciprocal tetraktys pattern using circles, labeling them with their respective number of slots, and changing their relative sizes:

This places the groups in the proper "tetraktys" order, going from smallest to largest, in two reciprocal "directions," as the dimension increases from 0, at the top, to 3, at the bottom, which works, except, when we number the elements. When we number them, element number 21,Sc, is the first element in the (blue) d group, instead of the first element in the (green) p group, as previously was the case. This is the vexing problem. How is it that the larger d group intercedes between the s and p groups like this? And the same thing happens at the next level; The first element at this level is the first element in the (red) f group, element number 57, La, not the first element in the (green) p group!
We can combine these groups, following the Stowe table format, placing the small s group in the middle of the larger groups:

This is good, but numbering the elements still requires us to jump from the center s group of a given set to the outer group of that set and work our way back to the center. This is so odd and just plain inexplicable!!!
In grappling with this, I came across Eric Scerri's articles and Youtube discussions on the periodic table, and he referred to the late Fernando Dufour, as the foremost researcher of the table, who designed a 3d model of it.
When I checked it out, I discovered that Dufour went beyond Stowe's design in that he removed the s groups from the linear succession, which is making it so difficult to understand how to format the table, consistent with all the constraints, and he placed them in their own dimension, the third dimension (the third dimension of space, not the tetraktys).
Wow, this does the trick, as shown in the next graphic, where I combined Stowe's and Dufour's ideas with my own:

In this new, abstract, version of the scalar-motion based Periodic Schematic of the Elements, the s group elements are treated as transition elements, which connect the four dimensions of the Reciprocal Tetraktys.
The new schematic shows how the Bott periodicity (modulo 8) plays between the four dimensions, producing the interval 8 between the reciprocal sub-periods of the elements: 4 + 8 = 6+6 = 12; 12 + 8 = 10+10 = 20; 20 + 8 = 14+14 = 28 (or s|s; p|p; d|d; f|f). When the 2+6 (s+p) fundamental is added to each dimension's increased degree of freedom, the sub-periods are produced (8 + 0 = 8; 8 + 10 = 18; 8 + 24 = 32).
The abstraction hides the many details that are only implied, but, taking the s groups out of the linear sequence of elements, allows us to see that they are common to all the groups of a set. In the first instance, the transition from 0 to 1 dimension, the two p groups appear to be uniquely associated with the two s groups, but this is an illusion due to the fact that the p groups are the only members of that set. When the schematic transitions to dimension 2, the d group encircles the p group, and upon transitioning to dimension 3, the f group encircles both the d and p groups.
The rule is that the atomic number sequence always begins with the outermost group, through the s group, which is now understandable, given the schematic, even if it's not entirely clear how this is to be interpreted physically, yet.
Stay tuned!