As far as when the 3d reversals take place, it's no different than Larson's 1d reversals: it happens at the end of each unit, as can be seen clearly in the world line charts posted earlier.
Of course, the reversing arrows on the chart are to be understood as radii of expanding/contracting balls, not 1d lines, so the two boundaries are the spherical surface and the center point, where the "direction" reversals take place.
Thus, one unit of motion takes place as one cycle of oscillation over two units of time and is repeated continuously. In other words, there is one period of inward motion, followed by a period of outward motion in each cycle or sequence: 2/2, which can be written (1+1)/2, for a space oscillation, or 2/(1+1), for a time oscillation. When we combine them both we get our scalar motion equation.
Once we have these units of motion combining them is straightforward, giving us the marvelous results we've achieved so far.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
For vector motion, whether linear or rotational, the change in position or location over time that defines it must be uni-"directional." For linear motion, this means outward from a specified point, or inward toward a specified point. For rotational motion, this means a clockwise change of angle or a counter-clockwise change of angle. Unlike scalar motion, vector motion cannot proceed in the two "directions" of a given dimension, simultaneously. Think of changing sines and cosines describing rotation. They change in one "direction" and then reverse and change in the opposite "direction," as the rotation proceeds.
However, this is not so with scalar motion. A scalar expansion of a line expands in both "directions" of its dimension, simultaneously. When it reverses, it contracts in both "directions" simultaneously (21 "directions"). If it's two-dimensional scalar motion, it expands/contracts in both "directions" of its two dimensions (22 "directions"). If it's three-dimensional scalar motion, it expand/contracts in both "directions" of its three dimensions (23 "directions").
This much is very clear. Now, what is needed is to understand how we can find numbers with these same properties. It was problematic for the ancient Greeks that lengths could be found for every number, but numbers couldn't be found for every length. It took Western civilization a long time to meet that challenge, but it finally did, at least to the satisfaction of most people.
Yet, not long after that, it was discovered that nature sticks with whole numbers anyway, so our unit measures had to be adapted to nature somehow, which, as Xavier Borg shows, have the dimensions of motion; that is, the dimensions of space/time.
Consequently, given Larson's new system of scalar motion, and the LST system of vector motion, we need to differentiate them in terms of nature's space/time. Well, we know that vector motion requires an object to change location over time, while scalar motion does not, so it follows that scalar motion is prior to vector motion, and we've shown how that can be in our version of the standard model of particle physics.
Unfortunately, though, as we've seen demonstrated in this forum so recently, the vector motion number system has been crafted to describe nature's space/time in terms of vector spaces and vector algebra. The idea of scalar spaces and scalar algebra isn't even comprehensible to LST physicists and mathematicians.
Nevertheless, we have seen how genuine these concepts are, by demonstrating the one-to-one correspondence between the "directions" of the Tetraktys dimensions and those of Larson's cube. Moreover, we can show that the scalar expansion of the 2x2x2 cube contains multi-dimensional unit magnitudes.
These multi-dimensional units shed an entirely new light on the LST's multi-dimensional numbers, based on vector motion, used in the so-called "normed division algebras," upon which all the technology, engineering and science of Western civilization are based.
As incredible as it may seem, the fact is multi-dimensional scalar motion gives rise to multi-dimensional scalar numbers and the algebra to add, multiply, subtract and divide them. Years ago, UofU math professor, Bob Palais, attended one of our ISUS meetings in SLC, and he and I had several follow up discussions. I tried to explain the idea of scalar numbers to him, but, at that point, the subject was not so developed in my own mind. He listened politely, and then asked me what the square of some of the numbers were. When I tried to square them, I failed and that was that, as far as he was concerned. We never met again.
I don't remember why I failed, because it seems trivial now, but it may have been due to not understanding the concept of "unit." What we mean by multi-dimensional is multi-dimensional units, the three listed in the previous post.
It's not that they are multi-dimensional in terms of orthogonal directions. That's a vector motion based concept. And it's not that they are multi-dimensional in terms of the wedge products of multivectors in Geometric Algebra. It's that they are the concurrent unit magnitudes of the expanding/contracting 2x2x2 stack of unit cubes - the three radii.
Larson thought of scalar magnitudes in terms of space or time displacement: s/t = 1/1, the unit speed, or datum, of the system, has zero displacement, but "direction" reversals in the expansion of space or time (two observables) led him to quantify speeds in terms of time displacement s/t = 1/(n>1) and space displacement, s/t = (n>1)/1; that is, displacement from unity in the numerator or denominator.
Of course, this is just the set of rational numbers, but with a special twist, where the displacements are inverse units in two, opposite "directions," instead of the fractions of a whole:
s/t = 1/2, 1/1, 2/1, in terms of speed displacements, are equivalent to -1, 0, +1, not .5, 1, 2.
Therefore, in terms of our 1d unit, √(12+02+02) = √1, the possibilities are:
1(√1)/2(√1), 1(√1)/1(√1), 2(√1)/1(√1) = -1, 0, +1
but in terms of our 2d unit, √(12+12+02) = √2, the possibilities are:
1(√2)/2(√2), 1(√2)/1(√2), 2(√2)/1(√2) = -1(√2), 0, +1(√2),
and for 3d, √(12+12+12) = √3, they are:
1(√3)/2(√3), 1(√3)/1(√3), 2(√3)/1(√3) = -1(√3), 0, +1(√3),
However, while the use of polarity signs above indicates the opposite "directions" of the numbers, it hides the inverse character of the opposite terms. To avoid this problem and clarify it a bit, let's revert to the rational form of the numbers and place the appropriate inverses under the ratios and then the displacement values under those:
...............1d -------------------------------------2d---------------------------------------3d
√1/2√1, √1/√1, 2√1/√1 <------------>√2/√8, √2/√2, √8/√2 <------------>√3/√12, √3/√3, √12/√3
.5______1_______2 <------------------> .5____1_____2 <------------------> .5____1____2
-1______0______+1<------------------> -1____0____+1 <-----------------> -1____0____+1
Now, we can see the inverse nature of the opposite terms, and , when we square n to eliminate the radicals, and write the difference between numerator and denominator (i.e. the displacement), adding the polarity signs, we can see the dimensional progressions:
1d = -n2, ...-3, -2, -1, 0, 1, 2, 3, ...n2
2d = -n2, ...-18, -8, -2, 0, 2, 8, 18, ...n2
3d = -n2, ...-27, -12, -3, 0, 3, 12, 27, ...n2
One might argue that the squaring operation removes the negative signs, and that's true, but only because, as no less a light than Sir William Rowan Hamilton pointed out, the rules of algebra have been crafted as an art, not a science. He wanted to put algebra on as sound a footing as we find for geometry. He wrote in his essay on the Science of Pure Time:
In our case, we simply add the negative sign to the square of n, as a shorthand symbol of the scientific, reciprocal, "direction," rules of the art be damned. The important thing to understand here is that the scalar expansion of three dimensional numbers, as quantities (2x2x2), entails three "units," not just one.
However, this is not so with scalar motion. A scalar expansion of a line expands in both "directions" of its dimension, simultaneously. When it reverses, it contracts in both "directions" simultaneously (21 "directions"). If it's two-dimensional scalar motion, it expands/contracts in both "directions" of its two dimensions (22 "directions"). If it's three-dimensional scalar motion, it expand/contracts in both "directions" of its three dimensions (23 "directions").
This much is very clear. Now, what is needed is to understand how we can find numbers with these same properties. It was problematic for the ancient Greeks that lengths could be found for every number, but numbers couldn't be found for every length. It took Western civilization a long time to meet that challenge, but it finally did, at least to the satisfaction of most people.
Yet, not long after that, it was discovered that nature sticks with whole numbers anyway, so our unit measures had to be adapted to nature somehow, which, as Xavier Borg shows, have the dimensions of motion; that is, the dimensions of space/time.
Consequently, given Larson's new system of scalar motion, and the LST system of vector motion, we need to differentiate them in terms of nature's space/time. Well, we know that vector motion requires an object to change location over time, while scalar motion does not, so it follows that scalar motion is prior to vector motion, and we've shown how that can be in our version of the standard model of particle physics.
Unfortunately, though, as we've seen demonstrated in this forum so recently, the vector motion number system has been crafted to describe nature's space/time in terms of vector spaces and vector algebra. The idea of scalar spaces and scalar algebra isn't even comprehensible to LST physicists and mathematicians.
Nevertheless, we have seen how genuine these concepts are, by demonstrating the one-to-one correspondence between the "directions" of the Tetraktys dimensions and those of Larson's cube. Moreover, we can show that the scalar expansion of the 2x2x2 cube contains multi-dimensional unit magnitudes.
These multi-dimensional units shed an entirely new light on the LST's multi-dimensional numbers, based on vector motion, used in the so-called "normed division algebras," upon which all the technology, engineering and science of Western civilization are based.
As incredible as it may seem, the fact is multi-dimensional scalar motion gives rise to multi-dimensional scalar numbers and the algebra to add, multiply, subtract and divide them. Years ago, UofU math professor, Bob Palais, attended one of our ISUS meetings in SLC, and he and I had several follow up discussions. I tried to explain the idea of scalar numbers to him, but, at that point, the subject was not so developed in my own mind. He listened politely, and then asked me what the square of some of the numbers were. When I tried to square them, I failed and that was that, as far as he was concerned. We never met again.
I don't remember why I failed, because it seems trivial now, but it may have been due to not understanding the concept of "unit." What we mean by multi-dimensional is multi-dimensional units, the three listed in the previous post.
It's not that they are multi-dimensional in terms of orthogonal directions. That's a vector motion based concept. And it's not that they are multi-dimensional in terms of the wedge products of multivectors in Geometric Algebra. It's that they are the concurrent unit magnitudes of the expanding/contracting 2x2x2 stack of unit cubes - the three radii.
Larson thought of scalar magnitudes in terms of space or time displacement: s/t = 1/1, the unit speed, or datum, of the system, has zero displacement, but "direction" reversals in the expansion of space or time (two observables) led him to quantify speeds in terms of time displacement s/t = 1/(n>1) and space displacement, s/t = (n>1)/1; that is, displacement from unity in the numerator or denominator.
Of course, this is just the set of rational numbers, but with a special twist, where the displacements are inverse units in two, opposite "directions," instead of the fractions of a whole:
s/t = 1/2, 1/1, 2/1, in terms of speed displacements, are equivalent to -1, 0, +1, not .5, 1, 2.
Therefore, in terms of our 1d unit, √(12+02+02) = √1, the possibilities are:
1(√1)/2(√1), 1(√1)/1(√1), 2(√1)/1(√1) = -1, 0, +1
but in terms of our 2d unit, √(12+12+02) = √2, the possibilities are:
1(√2)/2(√2), 1(√2)/1(√2), 2(√2)/1(√2) = -1(√2), 0, +1(√2),
and for 3d, √(12+12+12) = √3, they are:
1(√3)/2(√3), 1(√3)/1(√3), 2(√3)/1(√3) = -1(√3), 0, +1(√3),
However, while the use of polarity signs above indicates the opposite "directions" of the numbers, it hides the inverse character of the opposite terms. To avoid this problem and clarify it a bit, let's revert to the rational form of the numbers and place the appropriate inverses under the ratios and then the displacement values under those:
...............1d -------------------------------------2d---------------------------------------3d
√1/2√1, √1/√1, 2√1/√1 <------------>√2/√8, √2/√2, √8/√2 <------------>√3/√12, √3/√3, √12/√3
.5______1_______2 <------------------> .5____1_____2 <------------------> .5____1____2
-1______0______+1<------------------> -1____0____+1 <-----------------> -1____0____+1
Now, we can see the inverse nature of the opposite terms, and , when we square n to eliminate the radicals, and write the difference between numerator and denominator (i.e. the displacement), adding the polarity signs, we can see the dimensional progressions:
1d = -n2, ...-3, -2, -1, 0, 1, 2, 3, ...n2
2d = -n2, ...-18, -8, -2, 0, 2, 8, 18, ...n2
3d = -n2, ...-27, -12, -3, 0, 3, 12, 27, ...n2
One might argue that the squaring operation removes the negative signs, and that's true, but only because, as no less a light than Sir William Rowan Hamilton pointed out, the rules of algebra have been crafted as an art, not a science. He wanted to put algebra on as sound a footing as we find for geometry. He wrote in his essay on the Science of Pure Time:
So it is here. The confusion of thought, which comes into play here is, as Hestenes has pointed out, that there are two interpretations of number, a quantitative interpretation and an operational one, where the first is a measure of how much or how many, and the second defines a relation between different quantities. It is the second, or operational interpretation, which Larson employs in his concept of "speed displacements" that we are using here. The difference between the denominator and the numerator can be either positive or negative, depending on which is larger, but that is an algebraic rule for convenience in tracking the "direction" of numbers, and it doesn't countervail the science of reciprocity.The thing aimed at, is to improve the Science, not the Art nor the Language of Algebra. The imperfections sought to be removed, are confusions of thought, and obscurities or errors of reasoning; not difficulties of application of an instrument, nor failures of symmetry in expression. And that confusions of thought, and errors of reasoning, still darken the beginnings of Algebra, is the earnest and just complaint of sober and thoughtful men, who in a spirit of love and honour have studied Algebraic Science, admiring, extending, and applying what has been already brought to light, and feeling all the beauty and consistence of many a remote deduction, from principles which yet remain obscure, and doubtful.
In our case, we simply add the negative sign to the square of n, as a shorthand symbol of the scientific, reciprocal, "direction," rules of the art be damned. The important thing to understand here is that the scalar expansion of three dimensional numbers, as quantities (2x2x2), entails three "units," not just one.
Re: Meeting a Terrific Challenge
I hope I've been able to clear up the confusion that exists over the use of the word unit. It happens, because we use it in different ways to mean different things. We refer to the unit progression, meaning unit motion or one unit of space for one unit of time, or s/t =1/1. We refer to unit displacement, in the "directions" of each dimension, or s/t =1/2 and s/t =2/1, and we speak of a unit value, which can be one of three different values, √1, √2, √3.
So, it's easy to get confused in a conversation, if these different uses of the word aren't clear in our minds, but once they are clearly understood, the scalar motion system we are developing is simple and straightforward. The next step is combining these scalar units of motion, and exploring the relationships between them. As they say, great things can often proceed from small and simple means. One of those great things is the emergence of two sectors of the physical universe, the one we call the material sector, and the other, its reciprocal, we call the cosmic sector.
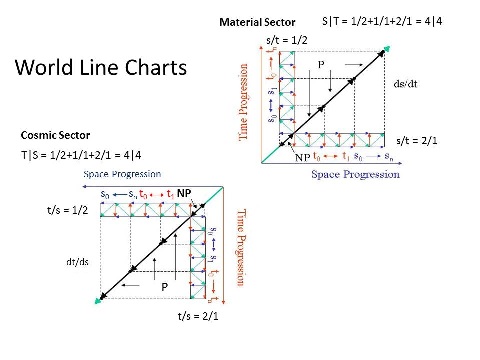
That these two sectors emerge logically and mathematically from the world line chart (re-posted above for convenient reference), where the space and time progressions are plotted orthogonally, for one sector, and the reciprocal sector plots are obtained by a 180 degree rotation of the line of unit space/time progression (heavy black arrows), is remarkable in itself.
From the chart of the two sectors, we can see that the high-speed side of one sector is the reciprocal of the low-speed side of the other and vice-versa. Thus, we obtain two reciprocal versions of the equation combining the low and high-speed oscillations, one for each sector:
1) Material sector equation: S|T = 1/2 + 1/1 + 2/1 = 4|4 num,
2) Cosmic sector equation: T|S = 1/2 + 1/1 + 2/1 = 4|4 num,
where num stands for natural units of motion.
Again, as Larson pointed out, the minimum cycle is two units, one inward unit over a unit of time (space), followed by one outward unit over a second unit of time (space), or s/t = 2/2 and t/s = 2/2, which are more clearly understood as s/t = (1+1)/2 and t/s = 2/(1+1), when the two reversing units are counted separately. Recalling how often the number 4 (or 2 squared) shows up in fundamental equations, causes us to wonder if there isn't a connection here.
With this much understood, though, we can proceed to combine these fundamental units, using the two equations, and at the same time we recognize that the implications are profound. First of all, the equations not only define the lowest common denominator for the two sectors; that is, a combination of one low-speed oscillation with one high-speed oscillation, but also this combination would have to be identified with the photon of the system, since the contribution of each of the non-reversing components produces the light speed of the combo, making it a combo oscillating in space and time, while propagating at unit speed.
Hence, the photon in both sectors becomes the basic building block of the theoretical universe of motion, and we have the scalar equations to help us employ it as such. To say that this simple and straightforward development of the consequences of the fundamental postulates of the reciprocal system is important or highly significant or wonderful would be an understatement. It's revolutionary.
So, it's easy to get confused in a conversation, if these different uses of the word aren't clear in our minds, but once they are clearly understood, the scalar motion system we are developing is simple and straightforward. The next step is combining these scalar units of motion, and exploring the relationships between them. As they say, great things can often proceed from small and simple means. One of those great things is the emergence of two sectors of the physical universe, the one we call the material sector, and the other, its reciprocal, we call the cosmic sector.

That these two sectors emerge logically and mathematically from the world line chart (re-posted above for convenient reference), where the space and time progressions are plotted orthogonally, for one sector, and the reciprocal sector plots are obtained by a 180 degree rotation of the line of unit space/time progression (heavy black arrows), is remarkable in itself.
From the chart of the two sectors, we can see that the high-speed side of one sector is the reciprocal of the low-speed side of the other and vice-versa. Thus, we obtain two reciprocal versions of the equation combining the low and high-speed oscillations, one for each sector:
1) Material sector equation: S|T = 1/2 + 1/1 + 2/1 = 4|4 num,
2) Cosmic sector equation: T|S = 1/2 + 1/1 + 2/1 = 4|4 num,
where num stands for natural units of motion.
Again, as Larson pointed out, the minimum cycle is two units, one inward unit over a unit of time (space), followed by one outward unit over a second unit of time (space), or s/t = 2/2 and t/s = 2/2, which are more clearly understood as s/t = (1+1)/2 and t/s = 2/(1+1), when the two reversing units are counted separately. Recalling how often the number 4 (or 2 squared) shows up in fundamental equations, causes us to wonder if there isn't a connection here.
With this much understood, though, we can proceed to combine these fundamental units, using the two equations, and at the same time we recognize that the implications are profound. First of all, the equations not only define the lowest common denominator for the two sectors; that is, a combination of one low-speed oscillation with one high-speed oscillation, but also this combination would have to be identified with the photon of the system, since the contribution of each of the non-reversing components produces the light speed of the combo, making it a combo oscillating in space and time, while propagating at unit speed.
Hence, the photon in both sectors becomes the basic building block of the theoretical universe of motion, and we have the scalar equations to help us employ it as such. To say that this simple and straightforward development of the consequences of the fundamental postulates of the reciprocal system is important or highly significant or wonderful would be an understatement. It's revolutionary.
Re: Meeting a Terrific Challenge
Not yet.
Please identify all of the meanings of the "unit" on your diagram for the 4 colors of arrows and the gray dashed line (including angles and lengths of arrows) P.S.
If you choose to edit this diagram, PLEASE do not save it in the lossy JPEG format !
Re: Meeting a Terrific Challenge
Okay:
Gray dashed lines: The two units of space and time comprising one unit (cycle) of motion (s/t = (1+1)/2 and 2/(1+1)).
Black diagonal arrows: Unit space/time progression; that is, one unit of space increase for one unit of time increase (s/t = 1/1). Although, the length of the black arrows is two units long.
Red vertical arrows: Unit time progression.
Blue horizontal arrows: Unit space progression.
Green vertical arrows: Unit space reversals.
Green horizontal arrows: Unit time reversals.
Red down arrow: Reciprocal space progression.
Blue left arrow: reciprocal time progression.
Now, after I posted the graphic for the two world line charts, I realized that it was outdated. When I first conceived of it, I wasn't thinking in terms of rotating the entire chart to obtain the reciprocal world line, but only the unit progression arrows. This generated an incorrect reciprocal progression, where the "direction" of reciprocal space progression is directly opposite the "direction" of the space progression, and the same for time.
However, when the entire chart is rotated to plot the reciprocal, the "direction" of the vertical time progression rotates to oppose the "direction" of the horizontal space progression, and the "direction" of the horizontal space progression rotates to oppose the "direction" of the time progression in the vertical. I intend to update the graphic as soon as I can.
Another thing to note is that even though the two plots (space and time reversals) are shown symmetrically, it isn't meant to imply that they happen simultaneously. As Larson stressed, the number of locations where space (time) reversals occur, past or future, is outside the scope of the system. We can only proceed on the basis of what can happen does happen, without recourse to a knowledge of why, how or where (when).
Gray dashed lines: The two units of space and time comprising one unit (cycle) of motion (s/t = (1+1)/2 and 2/(1+1)).
Black diagonal arrows: Unit space/time progression; that is, one unit of space increase for one unit of time increase (s/t = 1/1). Although, the length of the black arrows is two units long.
Red vertical arrows: Unit time progression.
Blue horizontal arrows: Unit space progression.
Green vertical arrows: Unit space reversals.
Green horizontal arrows: Unit time reversals.
Red down arrow: Reciprocal space progression.
Blue left arrow: reciprocal time progression.
Now, after I posted the graphic for the two world line charts, I realized that it was outdated. When I first conceived of it, I wasn't thinking in terms of rotating the entire chart to obtain the reciprocal world line, but only the unit progression arrows. This generated an incorrect reciprocal progression, where the "direction" of reciprocal space progression is directly opposite the "direction" of the space progression, and the same for time.
However, when the entire chart is rotated to plot the reciprocal, the "direction" of the vertical time progression rotates to oppose the "direction" of the horizontal space progression, and the "direction" of the horizontal space progression rotates to oppose the "direction" of the time progression in the vertical. I intend to update the graphic as soon as I can.
Another thing to note is that even though the two plots (space and time reversals) are shown symmetrically, it isn't meant to imply that they happen simultaneously. As Larson stressed, the number of locations where space (time) reversals occur, past or future, is outside the scope of the system. We can only proceed on the basis of what can happen does happen, without recourse to a knowledge of why, how or where (when).
Re: Meeting a Terrific Challenge
One thing we haven't talked about much, in connection with combining units of motion (meaning the unit oscillation, where s/t = (1+1)/2 or s/t = 2/(1+1)), is the fundamental concepts of point, line, plane and volume.
If we start with one point, considering it our fundamental location, in a 3d reference system, then we require two points, not located at the same position, to define a line between them. It requires three points, located at unique positions, not all on a line, to define a plane, and four points, located at unique positions not on a line or all on a plane, to define a volume.
In the development of the LRC's RSt, we have defined photons as a combination of two unit oscillations, schematically depicted as a dumbbell, a 1d combination of s/t = (1+1)/2 and s/t = 2/(1+1), two oscillating points, if you will. Joining multiple instances of these 1d entities, in parallel, doesn't affect the geometry, but joining three of them end-to-end forms a 2d entity, a plane, just as a minimum of three points, not on a line, are required to define a 2d plane.
These 2d "planes" enabled us to define the leptons and quarks of the LST's standard model, an empirically derived model of "elementary" particles. In the next step in the development, we were able to combine four of these "planes" into a tetrahedron figure, a 3d volume if you will, analogous to the minimum number of four points required to define a volume, in a 3d fixed reference system.
Consequently, we have 1, 2 and 3 dimensional combinations of scalar motion, which can then be combined to form all the constituents of the observed periodic table, and that's not all. To me, this seems logical and straightforward. If someone can point out the fallacy of it, I would be most grateful, since wasting my time and the time of others on BS, is not what I want to do.
If we start with one point, considering it our fundamental location, in a 3d reference system, then we require two points, not located at the same position, to define a line between them. It requires three points, located at unique positions, not all on a line, to define a plane, and four points, located at unique positions not on a line or all on a plane, to define a volume.
In the development of the LRC's RSt, we have defined photons as a combination of two unit oscillations, schematically depicted as a dumbbell, a 1d combination of s/t = (1+1)/2 and s/t = 2/(1+1), two oscillating points, if you will. Joining multiple instances of these 1d entities, in parallel, doesn't affect the geometry, but joining three of them end-to-end forms a 2d entity, a plane, just as a minimum of three points, not on a line, are required to define a 2d plane.
These 2d "planes" enabled us to define the leptons and quarks of the LST's standard model, an empirically derived model of "elementary" particles. In the next step in the development, we were able to combine four of these "planes" into a tetrahedron figure, a 3d volume if you will, analogous to the minimum number of four points required to define a volume, in a 3d fixed reference system.
Consequently, we have 1, 2 and 3 dimensional combinations of scalar motion, which can then be combined to form all the constituents of the observed periodic table, and that's not all. To me, this seems logical and straightforward. If someone can point out the fallacy of it, I would be most grateful, since wasting my time and the time of others on BS, is not what I want to do.
Re: Meeting a Terrific Challenge
Given that the identification of the 1d, 2d and 3d scalar motion combinations with the bosons (1d), leptons (2d) and hadrons (3d) of the LST's standard model of particle physics, explained in the previous post, is acceptable (no one seems to be taking exception so far), I would like to show next how our scalar motion equations support this "toy model," if you will.
The LST community defines hadrons as subatomic particles that are bound by a "strong" force, while it defines leptons as subatomic particles that are not bound by a "strong" force. Bosons are not defined in terms of a "strong" force, but in terms of an integral quantum spin. Therefore, the fact that we can now define these particles simply in terms of the three dimensions of the fundamental postulates is a significant clarification, but it doesn't address the LST's error in concocting autonomous forces. As Larson has stressed so admirably, there can be no such thing, given the LST's own definition of the concept of force: It is simply a quantity of acceleration.
The LST's equations of electrical and gravitational force are formulated without reference to vector motion, whereas the equation for magnetic force is necessarily formulated in terms of electric current flow, but what they all have in common is the LST's concept of "charge." Electrons (positrons) "carry" negative (positive) charges, in this view, and, though no one in the community can say what that means exactly, whatever it means constitutes the foundation of our modern technological world.
The situation is quite different in the RST community. We know what a "charge" is. It is a scalar motion. Everything in the universe of nothing but motion is either a motion, a combination of motions, or a relation between them. The reason like charges repel, while unlike charges attract, is due to the fact that they are reciprocal motions. This fact is most simply demonstrated by our scalar motion equation:
1) S|T = 1/2 + 1/1 + 2/1 = 4|4 num,
where num stands for natural units of motion. This equation is the mathematical expression of the Material sector's world line chart, which we have been discussing. It combines one space oscillation (s/t = (1+1)/2) with one, reciprocal, time oscillation (s/t = 2/(1+1)), constituting the theory's photon. Now, adding more of one than of the other of these two unit oscillations, unbalances the equation. For example, the equation for the electron is:
S|T = 6/12 + 6/3 + 6/3 = 18|18 num, a negative "charge,"
while the equation for the positron is:
S|T = 3/6 + 3/6 + 12/6 = 18|18 num, an equal, but opposite, positive "charge."
Combining these two equations, we get:
S|T = 9/18 + 9/9 + 18/9 = 36|36 num.
The middle term, which shows the imbalance as the difference between numerator and denominator, is now indicating a balanced equation, eliminating both "charges."
Combining equations for two electrons. or two positrons, however, the difference in the middle term doubles to 12/6, for the two electrons, and 6/12, for the two positrons, forcing the two particles apart.
In the case of the proton & electron combination, the middle term of the proton is 10/13, a positive "charge" equal to that of the positron, so combining it with the electron's middle term, 6/3, gives us a total of 16/16, again eliminating the imbalance, or "charges."
The significance of treating "charges," as reciprocal motions like this, is profound indeed. Since, here, the "charges" of multiple protons in the atom are not opposing each other with a force, given by the formula, F = (qxq')/d2, which at the small distances of subparticles would be terrific, no "strong" force is required to overcome the proton-proton repulsion the atoms would otherwise be subject to. The repulsive force is simply not there. The combined proton-electron reciprocal motions balance out, eliminating the "charges" they possess individually.
The reason the combination of these two entities does not eliminate them, as in the case of electron - positron combination, is due to the fact that the proton is not just a 2d "plane" as is the positron, equal to the electron in every way, except in the "direction" of it's scalar motion, but is a 3d tetrahedron, consisting of three "planes," whose net "charge" is 10/13, and balancing it out, by the addition of the electron "charge" of 6/3, to total 16/16, does not affect the individual "charges" of the three-quarks, relative to each other.
While this is a simplified explanation of the actual interactions, involving reciprocity, chirality and helicity, it does serve to show how our new scalar equations support the scalar combinations of our toy model of quarks, leptons and hadrons, to the extent it has been carried out.
Again, however, it bears mentioning that, if a fatal fallacy has been overlooked, making it all BS, please feel free to point it out. I would be most grateful.
The LST community defines hadrons as subatomic particles that are bound by a "strong" force, while it defines leptons as subatomic particles that are not bound by a "strong" force. Bosons are not defined in terms of a "strong" force, but in terms of an integral quantum spin. Therefore, the fact that we can now define these particles simply in terms of the three dimensions of the fundamental postulates is a significant clarification, but it doesn't address the LST's error in concocting autonomous forces. As Larson has stressed so admirably, there can be no such thing, given the LST's own definition of the concept of force: It is simply a quantity of acceleration.
The LST's equations of electrical and gravitational force are formulated without reference to vector motion, whereas the equation for magnetic force is necessarily formulated in terms of electric current flow, but what they all have in common is the LST's concept of "charge." Electrons (positrons) "carry" negative (positive) charges, in this view, and, though no one in the community can say what that means exactly, whatever it means constitutes the foundation of our modern technological world.
The situation is quite different in the RST community. We know what a "charge" is. It is a scalar motion. Everything in the universe of nothing but motion is either a motion, a combination of motions, or a relation between them. The reason like charges repel, while unlike charges attract, is due to the fact that they are reciprocal motions. This fact is most simply demonstrated by our scalar motion equation:
1) S|T = 1/2 + 1/1 + 2/1 = 4|4 num,
where num stands for natural units of motion. This equation is the mathematical expression of the Material sector's world line chart, which we have been discussing. It combines one space oscillation (s/t = (1+1)/2) with one, reciprocal, time oscillation (s/t = 2/(1+1)), constituting the theory's photon. Now, adding more of one than of the other of these two unit oscillations, unbalances the equation. For example, the equation for the electron is:
S|T = 6/12 + 6/3 + 6/3 = 18|18 num, a negative "charge,"
while the equation for the positron is:
S|T = 3/6 + 3/6 + 12/6 = 18|18 num, an equal, but opposite, positive "charge."
Combining these two equations, we get:
S|T = 9/18 + 9/9 + 18/9 = 36|36 num.
The middle term, which shows the imbalance as the difference between numerator and denominator, is now indicating a balanced equation, eliminating both "charges."
Combining equations for two electrons. or two positrons, however, the difference in the middle term doubles to 12/6, for the two electrons, and 6/12, for the two positrons, forcing the two particles apart.
In the case of the proton & electron combination, the middle term of the proton is 10/13, a positive "charge" equal to that of the positron, so combining it with the electron's middle term, 6/3, gives us a total of 16/16, again eliminating the imbalance, or "charges."
The significance of treating "charges," as reciprocal motions like this, is profound indeed. Since, here, the "charges" of multiple protons in the atom are not opposing each other with a force, given by the formula, F = (qxq')/d2, which at the small distances of subparticles would be terrific, no "strong" force is required to overcome the proton-proton repulsion the atoms would otherwise be subject to. The repulsive force is simply not there. The combined proton-electron reciprocal motions balance out, eliminating the "charges" they possess individually.
The reason the combination of these two entities does not eliminate them, as in the case of electron - positron combination, is due to the fact that the proton is not just a 2d "plane" as is the positron, equal to the electron in every way, except in the "direction" of it's scalar motion, but is a 3d tetrahedron, consisting of three "planes," whose net "charge" is 10/13, and balancing it out, by the addition of the electron "charge" of 6/3, to total 16/16, does not affect the individual "charges" of the three-quarks, relative to each other.
While this is a simplified explanation of the actual interactions, involving reciprocity, chirality and helicity, it does serve to show how our new scalar equations support the scalar combinations of our toy model of quarks, leptons and hadrons, to the extent it has been carried out.
Again, however, it bears mentioning that, if a fatal fallacy has been overlooked, making it all BS, please feel free to point it out. I would be most grateful.
Re: Meeting a Terrific Challenge
As this most recent series of posts is in response to Horace's request for clarification on the LRC's development of its RST-based theory, and the world line charts have been used for this purpose, I think it's time to clarify something that is long overdue in that regard. Eleven years ago or so I introduced our version of the standard model of particle physics, based on the combinations of scalar motion units that we have been discussing. However, at that point in time I used the ideas, in part, which I got from the "braids" of Sundance Bilson-Thompson, as a guide.
Unfortunately, the braids are organized differently than what is reflected most in the world line charts, namely reciprocity. Instead of reciprocity, which is most important for us, the braids are organized around the chirality of the standard model. I should have tackled this disconnect a long time ago, but I let it go, afraid I might lose the connection with the empirical data of LST particle physics.
Nevertheless, I think it's time to straighten it out. In the graphic below, I've tried to simplify both the model as it now stands and the proposed reorganization of it to reflect the world line charts:
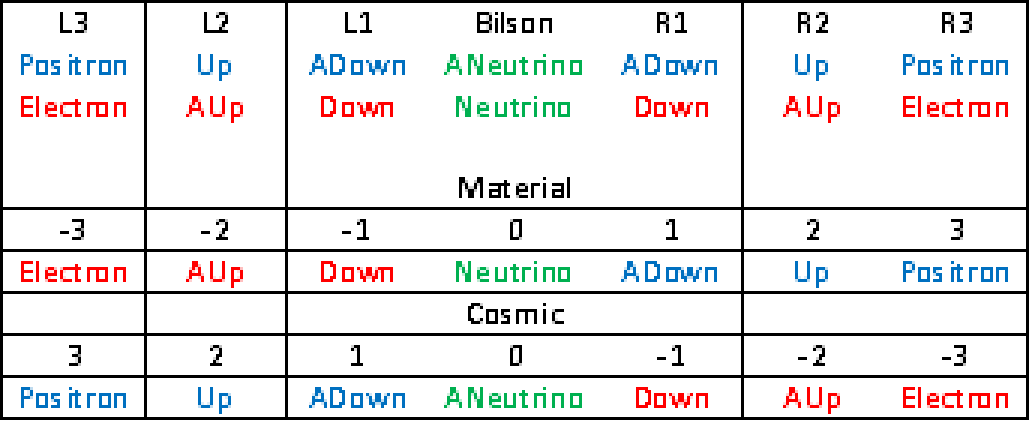
At the top of the graphic is the original braid-based model, and below it the new model, divided into two parts, one for the material sector and the other for the cosmic sector. The reciprocity is made clear, as one sector is viewed as the other one, but rotated around the vertical axis of the neutrinos (three column lines are missing from the graphic for some reason).
The left and right notion of the braids is replaced by the negative - positive "directions" of the number line, which in the material sector place the negative values on the left and the positive values on the right. This convention gets swapped in the cosmic sector by the 180 degree rotation.
I hope this is clear.
Unfortunately, the braids are organized differently than what is reflected most in the world line charts, namely reciprocity. Instead of reciprocity, which is most important for us, the braids are organized around the chirality of the standard model. I should have tackled this disconnect a long time ago, but I let it go, afraid I might lose the connection with the empirical data of LST particle physics.
Nevertheless, I think it's time to straighten it out. In the graphic below, I've tried to simplify both the model as it now stands and the proposed reorganization of it to reflect the world line charts:

At the top of the graphic is the original braid-based model, and below it the new model, divided into two parts, one for the material sector and the other for the cosmic sector. The reciprocity is made clear, as one sector is viewed as the other one, but rotated around the vertical axis of the neutrinos (three column lines are missing from the graphic for some reason).
The left and right notion of the braids is replaced by the negative - positive "directions" of the number line, which in the material sector place the negative values on the left and the positive values on the right. This convention gets swapped in the cosmic sector by the 180 degree rotation.
I hope this is clear.
Re: Meeting a Terrific Challenge
I'm grateful for the many views these latest posts are getting, but wondering why the silence? I'm hoping the LRC research and development of its RSt are gaining in credibility, but I can't be sure without comments. Nevertheless, I want to press on, and I want to do so in my usual verbose way, since it helps me, when I have to review the course of the development, which I often have to do (with sincere apologies to my friend Horace).
One thing to notice in all this, I think, is how we have gone from the FPs to two elementary combinations of scalar motion (SUDR & TUDR), to a combination of them, as S|T (T|S) entities, and then combinations of these with additional Ss and Ts, to form the entities of our standard model of particle physics. With these combos in hand, we were able to combine them into the hadron combos of the first family, the neutron and proton, and from there to the elements of the wheel of motion (periodic table of elements).
This has been a course of deductive development, and has many features elaborated upon by Larson, who compared it to the course of inventive science pursued by the LST community. Those people are really smart. They stand on the shoulders of Bohr, Heisenberg, Dirac, Pauli, Schrödinger, Planck, Einstein, Feynman, and many other pioneers of quantum mechanics. However, they are at a severe disadvantage, not having access to a fundamental postulate from which to logically deduce their conclusions for testing.
They started with observation and proceeded to invent explanations. Larson started with the fundamental postulates and proceeded to observations. However, they were able to explain the observations of the atomic spectra, with their inventions, whereas Larson could not arrive at the logical deductions required, and had to "skip" that step in his logical development. Nehru has termed this as the RST's "glaring lacuna."
Nevertheless, in leaving this glaring gap in the development of his RSt, Larson determined that the periods of the periodic table of elements are 4n2, instead of the 2n2 periods of the LST's quantum mechanics. This was implemented via the two magnetic (2d) displacement values of his rotational system, modified by electric (1d) displacement values. He explains this system of rotational displacements in chapter 10 of Nothing But Motion.
When I was studying this chapter, I decided to try to fit his system into a set of concentric circles that I had also been studying, which belonged to the so-called Aztec Calendar Stone. This was inspired, when my friend and neighbor, John Pratt, had informed me that the center glyph of the stone, occupying the center circle, stood for "movement," or, as we would prefer to say, "motion."
Thus, I was soon able to fit Larson's system of scalar rotations into four concentric circles, using his 4n2 periods:
1) 4 x 12 = 4;
2) 4 x 22 = 16;
3) 4 x 32 = 36;
4) 4 x 42 = 64;
I called it the "Wheel of Motion," to differentiate it from a "table," and published an article on it in the ISUS Reciprocity Journal (Reciprocity XXVII, Number 1 (Spring, 1998), which is also available here.
Jan Sammer, who was at that time an active researcher in ISUS, had pointed out the early scientific struggle over this issue, in a paper entitled, Why is the Periodic Table Askew? Scientists were trying to fit chemical elements into table schemes, based on various number combinations. No less a light than Rydberg himself formulated a simple arithmetical rule, which he called the rule of 'quadratic groups,' based on the formula 2n²," writes Sammer, "...he postulated two periods of 2, two of 8, two of 18 and two of 32 elements."
Although this was promising way back then, the trouble was how to account for the first two of the four in the first period. According to Sammer, Rydberg tried to confront the challenge by assuming "...that there had to be two undiscovered elements between hydrogen and helium. Once scientists were able to prove that no such elements existed," however, "Rydberg’s rule of “quadratic groups” and his 32-member periods fell into disrepute." So much so, I guess, that Larson didn't even know about it, at least he didn't mention it in his works.
When he developed his own table, though, he filled in the first two slots of the first period with the observed neutrino and his unobserved massless neutron, which, while it didn't derail his theory, as Rdyberg's solution had his, that's probably because his RSt has never mounted the rails of mainstream physics in the first place.
With this as background, we are faced with the same challenge as Rydberg and Larson: if the first period contains four slots, what elements or sub-elements go in the first two? The important difference is that, in our development, we started, as Larson did, with combinations of preon units of scalar motion, which have been combined into a model of sub-atomic particles, the combinations of which should continue logically to further combine into the elements of the periodic table.
Not only this, but we have formulated a mathematical equation that should continue to apply all the way through the development, enabling us to express the elements, as well as the particles, in terms of units of natural motion. This means that the basic number of that fundamental expression, the number 4, should continue to figure prominently in our combinations of scalar motions and relations between them.
Well, happily that is the case, although I can't provide the details in this post. However, I have provided them in the Introduction thread of the LRC topic of this forum. In short, the first two entities of the wheel of motion are the Neutron and the Proton, then comes the combination of the two, called the Deuteron, and finally Deuterium. This almost seems obvious, since the beta decay of the Neutron leaves a Proton and emits an Electron and an anti-Neutrino. Since the anti-Neutrino does not figure directly in the combinations of scalar motion entities, the next logical entity in the first period would be the Proton, followed by the combination of it with the Neutron to form the Deuteron, which is the third entity of the four, Of course. combining the Deuteron with the Electron forms the fourth and last entity of the first period, Deuterium.
Now, mathematically, this works out as well: the first entity, the Neutron, consists of 44 units of motion. The second entity, the Proton, consists of 46 units, which, when combined with the Neutron, forms the third entity, the Deuteron, with 90 units. Finally, combining the Electron with a Deuteron forms Deuterium, with 108 units:
1) Neutron = 44 units;
2) Proton = 46 units;
3) Deuteron = 90 units (Neutron plus Proton)
4) Deuterium = 108 units (Neutron plus Proton plus Electron)
Total units of scalar motion in the first period = 288 units.
So, we see that the gap in the periodic table between H and He is a misunderstanding. There really is no gap, due to the fact that Deuterium is the last entity in the first period, whereas He and the rest of the noble elements initiate their respective periods. This is very clear in the wheel of motion, but not in the periodic table. In the format of the wheel, the expanding number of elements in each successive circle is easily and naturally accommodated, eliminating all the gaps in the table and the need to separate out certain elements to make the table manageable.
In the course of the LST's development, the observed table is explained in terms of atomic energy spectra, and then, later, using the principles of quantum mechanics learned from that effort and quantum field theory, the standard model of particle physics was developed. For our part, in the course of our development, we deduced the standard model and the periodic table and now must proceed to deduce the atomic spectra, or the relation between the various scalar motion combos that we have identified.
This will be a challenge, because, unlike Larson's development, or the LST's development, combining successive numbers of Deuterium (108 num) to obtain each successive element in the wheel doesn't provide the 4n2 or the 2n2 structure. We don't have Larson's two magnetic and 1 electric rotations, nor the LST's electron shells, clouds, orbitals or what have you.
Recall, however, how Randell Mills has shaken the LST community with his orbitspheres, removing a lot of the mystery of quantum mechanics, while tapping into a whole new universe of energy. This innovation simply replaced the Bohr orbiting electrons with a new concept of an electron surrounding the hydrogen proton and containing one photon. This essentially replaced the ascending angular momentum of electrons in concentric Bohr orbits, with equal magnitudes of angular plus spin momentum found in the circulating currents of smaller orbitspheres. It all came down to a preferred method of "quantizing momentum." In Mills' model, inverse energy states become possible, whereas they don't in the Bohr model.
The question is, "Does this new development in the LST community give us a clue on how to proceed with our own theoretical development? Will our method of "quantizing momentum," which we hinted at earlier (a year or so ago), lead us to the 4n2 structure of the wheel of motion (periodic table)?"
Maybe. In the next post, we'll explore a new direction in this regard.
One thing to notice in all this, I think, is how we have gone from the FPs to two elementary combinations of scalar motion (SUDR & TUDR), to a combination of them, as S|T (T|S) entities, and then combinations of these with additional Ss and Ts, to form the entities of our standard model of particle physics. With these combos in hand, we were able to combine them into the hadron combos of the first family, the neutron and proton, and from there to the elements of the wheel of motion (periodic table of elements).
This has been a course of deductive development, and has many features elaborated upon by Larson, who compared it to the course of inventive science pursued by the LST community. Those people are really smart. They stand on the shoulders of Bohr, Heisenberg, Dirac, Pauli, Schrödinger, Planck, Einstein, Feynman, and many other pioneers of quantum mechanics. However, they are at a severe disadvantage, not having access to a fundamental postulate from which to logically deduce their conclusions for testing.
They started with observation and proceeded to invent explanations. Larson started with the fundamental postulates and proceeded to observations. However, they were able to explain the observations of the atomic spectra, with their inventions, whereas Larson could not arrive at the logical deductions required, and had to "skip" that step in his logical development. Nehru has termed this as the RST's "glaring lacuna."
Nevertheless, in leaving this glaring gap in the development of his RSt, Larson determined that the periods of the periodic table of elements are 4n2, instead of the 2n2 periods of the LST's quantum mechanics. This was implemented via the two magnetic (2d) displacement values of his rotational system, modified by electric (1d) displacement values. He explains this system of rotational displacements in chapter 10 of Nothing But Motion.
When I was studying this chapter, I decided to try to fit his system into a set of concentric circles that I had also been studying, which belonged to the so-called Aztec Calendar Stone. This was inspired, when my friend and neighbor, John Pratt, had informed me that the center glyph of the stone, occupying the center circle, stood for "movement," or, as we would prefer to say, "motion."
Thus, I was soon able to fit Larson's system of scalar rotations into four concentric circles, using his 4n2 periods:
1) 4 x 12 = 4;
2) 4 x 22 = 16;
3) 4 x 32 = 36;
4) 4 x 42 = 64;
I called it the "Wheel of Motion," to differentiate it from a "table," and published an article on it in the ISUS Reciprocity Journal (Reciprocity XXVII, Number 1 (Spring, 1998), which is also available here.
Jan Sammer, who was at that time an active researcher in ISUS, had pointed out the early scientific struggle over this issue, in a paper entitled, Why is the Periodic Table Askew? Scientists were trying to fit chemical elements into table schemes, based on various number combinations. No less a light than Rydberg himself formulated a simple arithmetical rule, which he called the rule of 'quadratic groups,' based on the formula 2n²," writes Sammer, "...he postulated two periods of 2, two of 8, two of 18 and two of 32 elements."
Although this was promising way back then, the trouble was how to account for the first two of the four in the first period. According to Sammer, Rydberg tried to confront the challenge by assuming "...that there had to be two undiscovered elements between hydrogen and helium. Once scientists were able to prove that no such elements existed," however, "Rydberg’s rule of “quadratic groups” and his 32-member periods fell into disrepute." So much so, I guess, that Larson didn't even know about it, at least he didn't mention it in his works.
When he developed his own table, though, he filled in the first two slots of the first period with the observed neutrino and his unobserved massless neutron, which, while it didn't derail his theory, as Rdyberg's solution had his, that's probably because his RSt has never mounted the rails of mainstream physics in the first place.
With this as background, we are faced with the same challenge as Rydberg and Larson: if the first period contains four slots, what elements or sub-elements go in the first two? The important difference is that, in our development, we started, as Larson did, with combinations of preon units of scalar motion, which have been combined into a model of sub-atomic particles, the combinations of which should continue logically to further combine into the elements of the periodic table.
Not only this, but we have formulated a mathematical equation that should continue to apply all the way through the development, enabling us to express the elements, as well as the particles, in terms of units of natural motion. This means that the basic number of that fundamental expression, the number 4, should continue to figure prominently in our combinations of scalar motions and relations between them.
Well, happily that is the case, although I can't provide the details in this post. However, I have provided them in the Introduction thread of the LRC topic of this forum. In short, the first two entities of the wheel of motion are the Neutron and the Proton, then comes the combination of the two, called the Deuteron, and finally Deuterium. This almost seems obvious, since the beta decay of the Neutron leaves a Proton and emits an Electron and an anti-Neutrino. Since the anti-Neutrino does not figure directly in the combinations of scalar motion entities, the next logical entity in the first period would be the Proton, followed by the combination of it with the Neutron to form the Deuteron, which is the third entity of the four, Of course. combining the Deuteron with the Electron forms the fourth and last entity of the first period, Deuterium.
Now, mathematically, this works out as well: the first entity, the Neutron, consists of 44 units of motion. The second entity, the Proton, consists of 46 units, which, when combined with the Neutron, forms the third entity, the Deuteron, with 90 units. Finally, combining the Electron with a Deuteron forms Deuterium, with 108 units:
1) Neutron = 44 units;
2) Proton = 46 units;
3) Deuteron = 90 units (Neutron plus Proton)
4) Deuterium = 108 units (Neutron plus Proton plus Electron)
Total units of scalar motion in the first period = 288 units.
So, we see that the gap in the periodic table between H and He is a misunderstanding. There really is no gap, due to the fact that Deuterium is the last entity in the first period, whereas He and the rest of the noble elements initiate their respective periods. This is very clear in the wheel of motion, but not in the periodic table. In the format of the wheel, the expanding number of elements in each successive circle is easily and naturally accommodated, eliminating all the gaps in the table and the need to separate out certain elements to make the table manageable.
In the course of the LST's development, the observed table is explained in terms of atomic energy spectra, and then, later, using the principles of quantum mechanics learned from that effort and quantum field theory, the standard model of particle physics was developed. For our part, in the course of our development, we deduced the standard model and the periodic table and now must proceed to deduce the atomic spectra, or the relation between the various scalar motion combos that we have identified.
This will be a challenge, because, unlike Larson's development, or the LST's development, combining successive numbers of Deuterium (108 num) to obtain each successive element in the wheel doesn't provide the 4n2 or the 2n2 structure. We don't have Larson's two magnetic and 1 electric rotations, nor the LST's electron shells, clouds, orbitals or what have you.
Recall, however, how Randell Mills has shaken the LST community with his orbitspheres, removing a lot of the mystery of quantum mechanics, while tapping into a whole new universe of energy. This innovation simply replaced the Bohr orbiting electrons with a new concept of an electron surrounding the hydrogen proton and containing one photon. This essentially replaced the ascending angular momentum of electrons in concentric Bohr orbits, with equal magnitudes of angular plus spin momentum found in the circulating currents of smaller orbitspheres. It all came down to a preferred method of "quantizing momentum." In Mills' model, inverse energy states become possible, whereas they don't in the Bohr model.
The question is, "Does this new development in the LST community give us a clue on how to proceed with our own theoretical development? Will our method of "quantizing momentum," which we hinted at earlier (a year or so ago), lead us to the 4n2 structure of the wheel of motion (periodic table)?"
Maybe. In the next post, we'll explore a new direction in this regard.
Re: Meeting a Terrific Challenge
The challenge of explaining the observed atomic spectra, as we have sought to overcome it at the LRC, has been intimidating, to say the least. We have our standard model of subatomic particles, consisting of S & T combos, making up 14 quarks and leptons, and we have the periods of our wheel of motion, consisting of atomic combos, making up 117 elements, but these all consist of natural units of motion, combined together, while the atomic spectra is a spectra of natural units of inverse motion, or energy, associated with them, in a very specific and identifiable way.
So far, our efforts to explain the Hydrogen spectra in terms of our scalar motion energy equation have paid off, but only in terms of the math. We have struggled to find a physical model comparable to the LST's Bohr Model (old QM), the Dirac model (new QM) or the Mills model (classical mechanics).
The problem, as explained earlier in this forum topic, is, unlike the LST, we haven't "quantized momentum." Indeed, we haven't even identified momentum in our system, yet. Momentum (quantity of (vector) motion), while an essential key to LST theory, plays no part in the theory of scalar motions that we have developed so far. However, we know it must emerge from the scalar combos at some point, if we are to progress with the development of our RSt.
The approach we've taken to this point is to tentatively identify the two, reciprocal, oscillations (space and time), making up our combos and posit that since the changing 2d areas of their volumes (either the cross sections or the spherical surfaces) compliment each other, the net 2d scalar motion (equivalent momentum) remains constant, for a given magnitude of the combo's total scalar motion. However, the details remain to be worked out.
In the meantime, the model of our atom, a tetrahedron, does not have a geometry that lends itself to combinations. It is an awkward and unwieldy geometry, with which to form combinations, especially given the high number of them we must handle. Therefore, instead of attempting to envision the geometry of these combos, it would be better to recognize that the same thing can be accomplished by increasing the magnitude of the original constituents of the tetrahedron.
On this basis, the first one, associated with Deuterium, is depicted in the usual way:
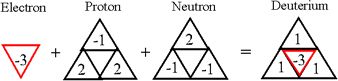
and successive elements can also be depicted in this way, but with their own numbers:
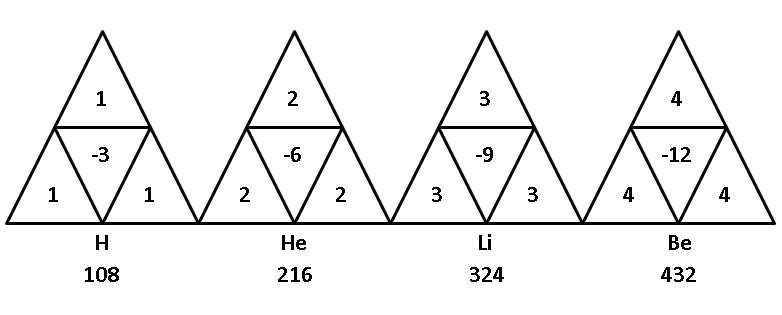
In other words, we can combine multiple quarks and leptons, instead of another instance of Deuterium, to form each successive element.
Also, notice that the total number of num is indicated below each element's symbol. Since, our theoretical photon consists of three S|T (T|S) units in parallel, we can conceive of photons absorbed by electrons, up to this limit of total atomic num. For example, H has a total of 108, so the 13.6 eV it takes to ionize it, can be divided into 108/12 (3x4) = 9 steps, with the energy of each step calculated as shown previously in the Introduction topic of this forum.
In the case of He, there are two electrons that can absorb photons in steps analogous to electron orbits, and with Li, there are three and so on up the line.
In the next post, we'll take a closer look at how all this might work.
So far, our efforts to explain the Hydrogen spectra in terms of our scalar motion energy equation have paid off, but only in terms of the math. We have struggled to find a physical model comparable to the LST's Bohr Model (old QM), the Dirac model (new QM) or the Mills model (classical mechanics).
The problem, as explained earlier in this forum topic, is, unlike the LST, we haven't "quantized momentum." Indeed, we haven't even identified momentum in our system, yet. Momentum (quantity of (vector) motion), while an essential key to LST theory, plays no part in the theory of scalar motions that we have developed so far. However, we know it must emerge from the scalar combos at some point, if we are to progress with the development of our RSt.
The approach we've taken to this point is to tentatively identify the two, reciprocal, oscillations (space and time), making up our combos and posit that since the changing 2d areas of their volumes (either the cross sections or the spherical surfaces) compliment each other, the net 2d scalar motion (equivalent momentum) remains constant, for a given magnitude of the combo's total scalar motion. However, the details remain to be worked out.
In the meantime, the model of our atom, a tetrahedron, does not have a geometry that lends itself to combinations. It is an awkward and unwieldy geometry, with which to form combinations, especially given the high number of them we must handle. Therefore, instead of attempting to envision the geometry of these combos, it would be better to recognize that the same thing can be accomplished by increasing the magnitude of the original constituents of the tetrahedron.
On this basis, the first one, associated with Deuterium, is depicted in the usual way:

and successive elements can also be depicted in this way, but with their own numbers:

In other words, we can combine multiple quarks and leptons, instead of another instance of Deuterium, to form each successive element.
Also, notice that the total number of num is indicated below each element's symbol. Since, our theoretical photon consists of three S|T (T|S) units in parallel, we can conceive of photons absorbed by electrons, up to this limit of total atomic num. For example, H has a total of 108, so the 13.6 eV it takes to ionize it, can be divided into 108/12 (3x4) = 9 steps, with the energy of each step calculated as shown previously in the Introduction topic of this forum.
In the case of He, there are two electrons that can absorb photons in steps analogous to electron orbits, and with Li, there are three and so on up the line.
In the next post, we'll take a closer look at how all this might work.