It's certainly understandable, if the ideas presented in the previous post above seem bizarre to the reader. Nevertheless, the development is logical and follows from the system's fundamental postulate. The basic idea follows from the broken symmetry of the quarks, which is quite apparent.
Unlike the leptons and neutrino, which are fully symmetrical, so that rotating their schematic symbols makes no change to their appearance, rotating the symbols of the quarks does change their appearance, due to the broken symmetry of their constituent S|T (T|S) units, and even though this schematic difference is meaningless from a physical standpoint, it does illustrate that there exists a lack of symmetry in the analogous physical attributes of the particles.
What I am asserting is that the broken symmetry in the physical attributes of the quarks may be due to the combinations of different unit sizes. It seems clear that a given LC can be based on any of the three units, √1, √2 or √3. Regardless of which unit size is considered, there are always the three radii associated with it, the radius of the inner, the middle and the outer balls, defined by the LC based on that unit size.
Each of the three sets of dimensional magnitudes, or values generated by these three possible LCs, contains one integer magnitude: √1, √4, √9, as shown below
For unit size = √1:
1) √((√1)2+(√1)2+(√1)2) = √(1+1+1) = √3;
2) √((√1)2+(√1)2+(√0)2) = √(1+1+0) = √2;
3) √((√1)2+(√0)2+(√0)2) = √(1+0+0) = √1;
For unit size = √2:
1) √((√2)2+(√2)2+(√2)2) = √(2+2+2) = √6;
2) √((√2)2+(√2)2+(√0)2) = √(2+2+0) = √4;
3) √((√2)2+(√0)2+(√0)2) = √(2+0+0) = √2;
For unit size = √3:
1) √((√3)2+(√3)2+(√3)2) = √(3+3+3) = √9;
2) √((√3)2+(√3)2+(√0)2) = √(3+3+0) = √6;
3) √((√3)2+(√0)2+(√0)2) = √(3+0+0) = √3;
The conjecture is that if one quark of a nucleon's three quarks, whose constituent S|T units are combos of LCs that are based on a √3 unit size, then the S|T units of the other two quarks would necessarily have to consist of √1 and √2 based LCs, in order to dimensionally balance the opposing scalar motions, and when a neutron under goes beta decay, the unit size of the transformed down quark's LCs would have to change size accordingly, forcing the others to change as well, in order to maintain dimensional balance.
While this may seem bizarre, I would submit that it's no more so than the observed physical properties and behavior of the nucleons themselves.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
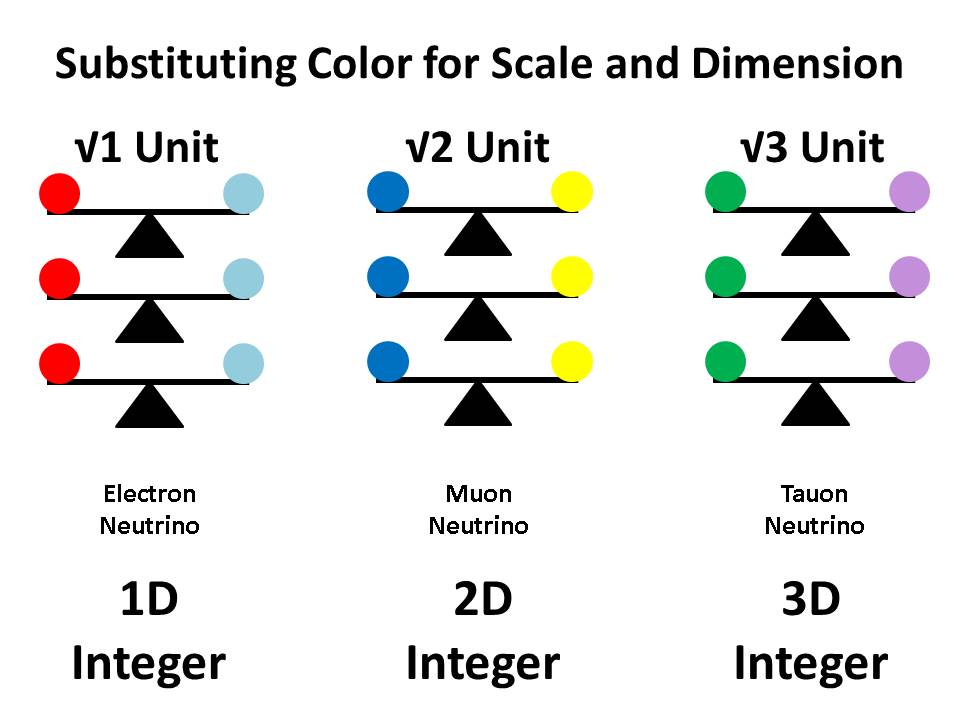
In the previous post above, I referred to the quarks in a nucleon as dimensionally balanced "color" charges, but I think the phrase is mis-leading, since their constituent Ss and Ts are all 3D. What we are comparing to color in them is the unique integer value of one of their three radii. The color red is assigned to the √1 based LC, the color blue to the √2 based LC and the color green to the √3 based LC.
On this basis, we can identify each of the three LCs by the color assigned to their integer-valued radius, so that a √1 size LC is red, √2 blue and √3 green, where a red LC is characterized by its 1d integer radius (1), a blue LC by its 2d integer radius (2) and a green LC by its 3d integer radius (3).
Of course, we are still handicapped by not knowing what the traditional equivalent of the natural unit is, since we've yet to determine, whether it is Larson's value, or Borg's value, or some other value.
Recently, the work of Brian Nelson has come to our attention, which pins down the mass of the nucleons' constituent quarks by numerical means, but to do so, he first derives a unit wavelength from Einstein's and Planck's equations, by recognizing the Pythagorean theorem relationship between rest mass and momentum and quantizing it (see here).
Interestingly enough, his conclusion is that mass and momentum are related, through the Pythagorean theorem, to a helical pattern of vector motion, a la Hestenes, although he doesn't mention him or the hypothetical zitterbewegung motion of the electron that Hestenes works with.
What he does do is combine the two energy equations into one equation by quantizing the energy of a unit wavelength.
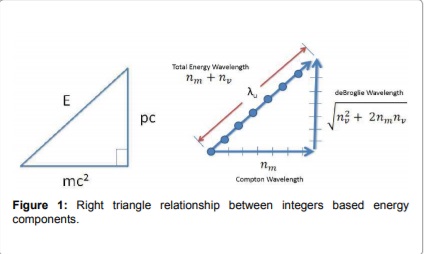
His work is based on the full Einstein equation which includes both the rest mast (mc2) and the momentum term (pc2) of the equation, or what we would call the scalar motion term (nm) and the vector motion term (nv).
These two energy components are summed as two integers of mass energy and kinetic energy in the hypotenuse, which integers are derived by assuming that we can start with a unit wavelength and divide it into smaller and smaller lengths, representing the harmonics of a fundamental frequency, as the energy increases. Plugging the total energy, as a sum of these two energy components, into the Pythagorean theorem, gives us a way to combine Planck's energy equation (E=hf) with Einstein's energy equation (E= mc2 + pc2).
Nelson writes: "The hypothesis states that elementary particles absorb precise quantities of kinetic energy in order to form integer multiples of their total energy wavelength in addition to their deBroglie wavelengths. This means that particles that bond, like the electron and proton with their respective rest masses (nme and nmp), share the same quantity of kinetic energy (𝑛𝑣) in order for their total energy wavelengths to share common factors."
In addition to his papers on this, available on his website, he explains it in a YouTube video here, and, in another video, he describes how the hypothesis, that "elementary particles share force carrier particles with precise quantities of energy in order to bond using integer multiples of their [total energy]," not only leads to a precise calculation of quark masses, but also explains how their total energy is not the same in the neutron and proton.
Based on Nelson's hypothesis, the total energy of the quarks actually changes, according to their number in the nucleons, because, the common kinetic energy, which they must share in order to bond, changes, depending on whether there are two of them or one of them in a given nucleon. In other words, in terms of the LST's standard model, the "gluon" energy binding the quarks, which constitutes most of the "mass" of the nucleon, is not the same in a proton as it is in a neutron, as shown in the graphic below:

Of course, in our RSt, we don't have "gluons," but we do have the 1, 2 and 3 "colored" LCs described above, each able to contribute its unique integral value to the combo's dimensional requirements. Whether this will work or not, I don't know yet, but I'm happy that it comes out of the logical development of the system.
On this basis, we can identify each of the three LCs by the color assigned to their integer-valued radius, so that a √1 size LC is red, √2 blue and √3 green, where a red LC is characterized by its 1d integer radius (1), a blue LC by its 2d integer radius (2) and a green LC by its 3d integer radius (3).
Of course, we are still handicapped by not knowing what the traditional equivalent of the natural unit is, since we've yet to determine, whether it is Larson's value, or Borg's value, or some other value.
Recently, the work of Brian Nelson has come to our attention, which pins down the mass of the nucleons' constituent quarks by numerical means, but to do so, he first derives a unit wavelength from Einstein's and Planck's equations, by recognizing the Pythagorean theorem relationship between rest mass and momentum and quantizing it (see here).
Interestingly enough, his conclusion is that mass and momentum are related, through the Pythagorean theorem, to a helical pattern of vector motion, a la Hestenes, although he doesn't mention him or the hypothetical zitterbewegung motion of the electron that Hestenes works with.
What he does do is combine the two energy equations into one equation by quantizing the energy of a unit wavelength.

His work is based on the full Einstein equation which includes both the rest mast (mc2) and the momentum term (pc2) of the equation, or what we would call the scalar motion term (nm) and the vector motion term (nv).
These two energy components are summed as two integers of mass energy and kinetic energy in the hypotenuse, which integers are derived by assuming that we can start with a unit wavelength and divide it into smaller and smaller lengths, representing the harmonics of a fundamental frequency, as the energy increases. Plugging the total energy, as a sum of these two energy components, into the Pythagorean theorem, gives us a way to combine Planck's energy equation (E=hf) with Einstein's energy equation (E= mc2 + pc2).
Nelson writes: "The hypothesis states that elementary particles absorb precise quantities of kinetic energy in order to form integer multiples of their total energy wavelength in addition to their deBroglie wavelengths. This means that particles that bond, like the electron and proton with their respective rest masses (nme and nmp), share the same quantity of kinetic energy (𝑛𝑣) in order for their total energy wavelengths to share common factors."
In addition to his papers on this, available on his website, he explains it in a YouTube video here, and, in another video, he describes how the hypothesis, that "elementary particles share force carrier particles with precise quantities of energy in order to bond using integer multiples of their [total energy]," not only leads to a precise calculation of quark masses, but also explains how their total energy is not the same in the neutron and proton.
Based on Nelson's hypothesis, the total energy of the quarks actually changes, according to their number in the nucleons, because, the common kinetic energy, which they must share in order to bond, changes, depending on whether there are two of them or one of them in a given nucleon. In other words, in terms of the LST's standard model, the "gluon" energy binding the quarks, which constitutes most of the "mass" of the nucleon, is not the same in a proton as it is in a neutron, as shown in the graphic below:
Of course, in our RSt, we don't have "gluons," but we do have the 1, 2 and 3 "colored" LCs described above, each able to contribute its unique integral value to the combo's dimensional requirements. Whether this will work or not, I don't know yet, but I'm happy that it comes out of the logical development of the system.
Re: Meeting a Terrific Challenge
In order for the idea of "colored" LCs to work as described in the previous entry, I think we must assume that a given S|T unit is comprised of one color of LC, not a mix. If this is correct, then it forces us to assume that, since a nucleon has to consist of all three colors, then the neutrinos of all three families (electron, muon and tau) are contributing to the quarks.
This condition would not need to hold for the electrons, since they need only consist of three one-dimensional S|T (T|S) units.
Yet, this line of reasoning leads to further consideration of the LC and its three radii. Recall that the LC is a mathematical object in three dimensions. It would be wonderful if nature worked in the same way; that is, expanding (contracting) in two "directions" of each dimension, resulting in a 2x2x2 stack of 8 unit cubes, in one unit of time.
However, this is not the case, but the 3d stack does define the radii of three balls, the inside, the middle and the outside balls, which radii happen to be √1, √2, and √3, and so we can identify what we are want to call three unit magnitudes of nature.
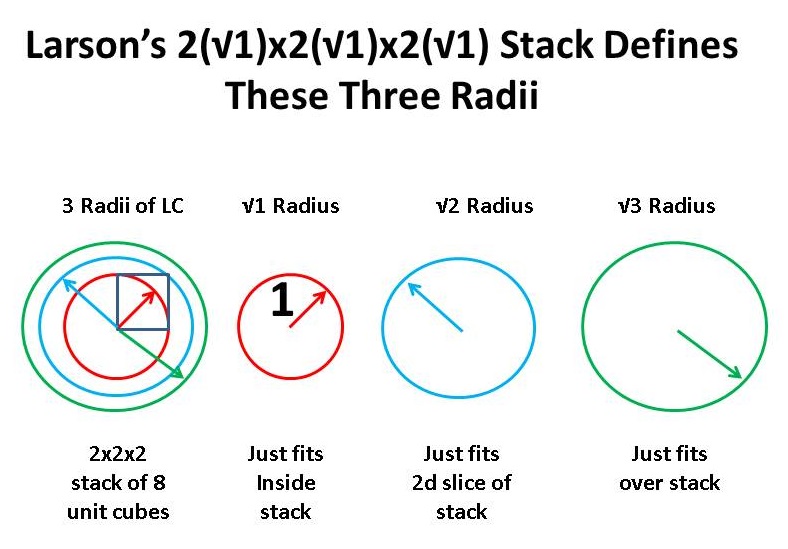
As everything in a universe of motion is either a motion, a combination of motions, or some relation between them, having these three unit motions to work with is perhaps the key to exploring the various configurations that appear possible.
If we change the unit in the stack from the first magnitude of √1, to √2, we get three magnitudes that are double the first, in terms of the new unit (√2):
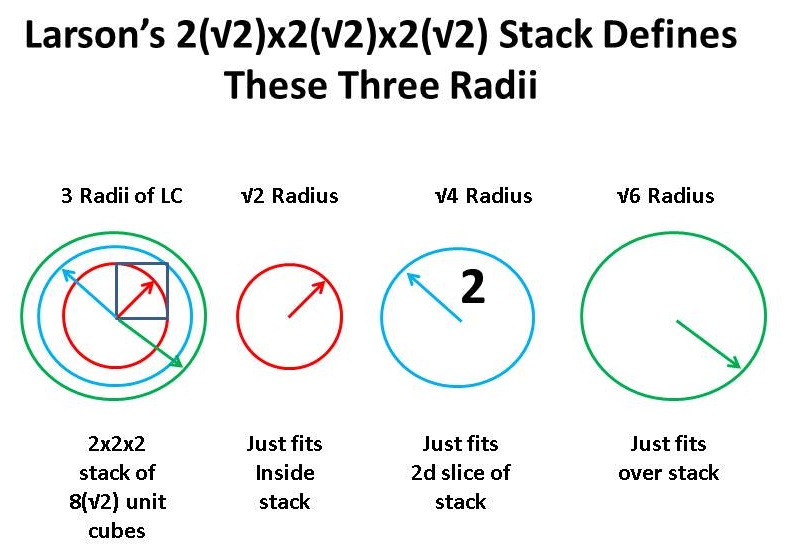
That is to say, √2 * √1 = √2; √2 * √2 = √4; √2 * √3 = √6. We can also see this in terms of the √3 unit LC:
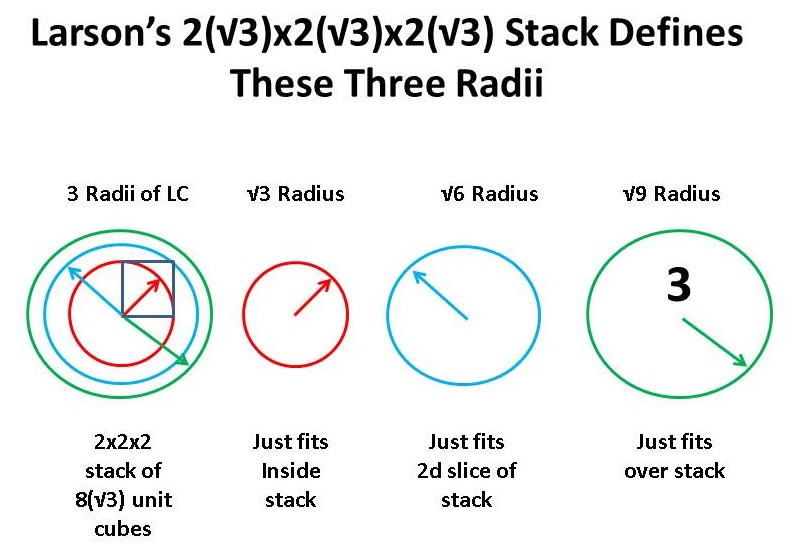
Now, we have √3 * √1 = √3; √3 * √2 = √6 and √3 * √3 = √9.
As noted previously, one member in each of these three sets, which is a multiple of the original set, turns out to be an integer-valued radius, the one, two or three-dimensional ball of their respective LC. They are denoted in the slides above.
Clearly, while the LCs mathematics has defined the geometry of the balls, it does not follow that they are dependent in anyway on an expanding/contracting stack. The significance of this observation is that the three radii, and multiples of them, can form S|T (T|S) units as discrete combinations of space and time (time and space) oscillations, just as we have combined them in our version of the standard model.
In a discrete universe, integer magnitudes are paramount, and as Brian Nelson has shown, things work out marvelously when we look for them. Maybe we are on the right track.
This condition would not need to hold for the electrons, since they need only consist of three one-dimensional S|T (T|S) units.
Yet, this line of reasoning leads to further consideration of the LC and its three radii. Recall that the LC is a mathematical object in three dimensions. It would be wonderful if nature worked in the same way; that is, expanding (contracting) in two "directions" of each dimension, resulting in a 2x2x2 stack of 8 unit cubes, in one unit of time.
However, this is not the case, but the 3d stack does define the radii of three balls, the inside, the middle and the outside balls, which radii happen to be √1, √2, and √3, and so we can identify what we are want to call three unit magnitudes of nature.

As everything in a universe of motion is either a motion, a combination of motions, or some relation between them, having these three unit motions to work with is perhaps the key to exploring the various configurations that appear possible.
If we change the unit in the stack from the first magnitude of √1, to √2, we get three magnitudes that are double the first, in terms of the new unit (√2):

That is to say, √2 * √1 = √2; √2 * √2 = √4; √2 * √3 = √6. We can also see this in terms of the √3 unit LC:

Now, we have √3 * √1 = √3; √3 * √2 = √6 and √3 * √3 = √9.
As noted previously, one member in each of these three sets, which is a multiple of the original set, turns out to be an integer-valued radius, the one, two or three-dimensional ball of their respective LC. They are denoted in the slides above.
Clearly, while the LCs mathematics has defined the geometry of the balls, it does not follow that they are dependent in anyway on an expanding/contracting stack. The significance of this observation is that the three radii, and multiples of them, can form S|T (T|S) units as discrete combinations of space and time (time and space) oscillations, just as we have combined them in our version of the standard model.

In a discrete universe, integer magnitudes are paramount, and as Brian Nelson has shown, things work out marvelously when we look for them. Maybe we are on the right track.
Re: Meeting a Terrific Challenge
Since Dewey Larson passed away, not only has the standard model of the LST's particle physics advanced considerably, in general, but particularly with regards to neutrinos. What's called "neutrino oscillation" has been observed and confirmed in several different experiments. For the LST community, this implies that neutrinos have a very small mass.
In fact, they think any given neutrino has three very small masses, and the most popular speculation is that these masses act like a mass sitting on a seesaw with a much heavier mass! They call this "credible supposition," because "reputable" scientists are currently testing this hypothesis (see here)!
Of course, their concept of the seesawing masses is not even close to ours, since the whole LST concept is radically different than the RST concept. Yet, the very fact that they have been led to the triality of the seesaw is quite delightful. Unfortunately, however, in order to explain it, they have to resort to ill or undefined concepts such as "force," "spin," "charge" and "mass."
In the LRC's RST-based theory, our RSt, if you will, there are three and only three neutrinos and they are massless. Furthermore, they each consist of three "massless" seesaws (see previous post above,) which are "balanced" in one sense, but not in another sense.
In the sense that they are balanced, we understand it as we do the inverse of a rational number, where one rational is on the positive side of 1/1 and its inverse is on the other side, an equal distance from 1/1, but in the opposite "direction." In the other sense, however, a rational number n/1 is far from equal to its inverse. In fact, it's n2 greater than its inverse!
These differences are important to understand, in a universe of motion, which is limited to no more than three dimensions. We've seen how great this works out for the mathematics of the one-dimensional case, such as electrical charge, because two, opposite, 1d lengths are naturally understood as equal and opposite. This is not the case, however, in higher dimensions. In two dimensions, the inverse of n2 is not "equal and opposite" that of n2. It's at least 16 times smaller (22/1 ÷ 1/22 = 16), in our quantum world! In three dimensions, the difference is even more startling. The inverse of the smallest rational cubed , 23/1, is 64 times smaller than it is (23/1 ÷1/23 = 64).
Nevertheless, physical entities are not composed of discrete numbers, even though it would be a whole lot easier if they were. In our theory, the discrete numbers help define the physical entities and thus help us to understand them. This is especially helpful in understanding how the dynamics of pulsating volumes are mistaken for those of impossible rotations, treated as quantum spin. Originally, for the LST community, this quantum magnitude was thought of as an "equal but opposite" property, necessary to distinguish between two electrons sharing the same orbit around an atomic nucleus, but having no true classical interpretation that could be found to fit the requirements (this caveat is routinely mentioned in LST presentations to the lay public, with no reference to the work stoppage it should invoke. This is another instance like that of the vacuum catastrophe of quantum field theory (see here).)
In the case of the neutrinos, the concept of quantum spin is used to differentiate between observed neutrinos and something called "sterile neutrinos." These are postulated neutrinos that interact with "right-handed" particles, something which has never been observed, since observed neutrinos only interact with left-handed particles and right-handed anti-particles. The postulated neutrinos are called "sterile," because, unlike observed neutrinos, there is no known lepton particle to associate with them.
I suspect that this has to do with the nature of anti-neutrinos in the cosmic sector of the RST-based theories, but I'm not sure just how that might work yet. What's so interesting at this point is the three internal masses that the LST community feels might actually account for the observed neutrino oscillation, through the "seesaw mechanism."
This mechanism, as they call it, creates a superposition of the neutrino's internal masses, whose matter waves vary slightly, creating a beat frequency that varies with time (see here.)
The analogy used in the video linked to above, where rotating arrows are used to explain the idea of three internal neutrino masses works well, but the underlying idea that comes into play, as the seesaw mechanism, is missing. That idea coupled with the fundamental concept of quantum mechanics, the dual particle/wave nature of matter, which de Broglie first showed, the so-called matter wave, is more clearly explained in the following video, where Kenneth Long of Imperial College of London explains it here.
The seesaw bit comes into play, at the point where he says, "The neutrino is neutral, so I can try to write that as the sum of two neutral states...." These two "neutral states" are neutral in the sense of charge, but not in terms of mass, which varies, and if their masses are not equal, neither are their associated matter wavelengths, resulting in the time-varying momentum compared to that of the non time-varying momentum of the electron.
Again, the idea of dimension comes into play here, because charge is one-dimensional and thus "equal and opposite" in the seesaw analogy, but mass is three-dimensional and thus far from "equal" on the seesaw.
Of course, if there are three such internal masses, as is supposed, then one has to treat them two at a time, just like we do in calculating the current in parallel electric circuits, where we take two paths at a time, and do the product over the sum to get an effective resistance that can then be paired up with the next element and the procedure repeated as necessary to arrive at the final answer.
For those of you following the LRC's RSt in these posts, your interest will no doubt be piqued once again, as, here, the RST's universe of motion clarifies, in very simple terms, something very fundamental, which I'll try to get to next time: Larson's central idea of space/time and time/space "speed displacements" is not only germane to the current topic, but is ultimately related through this "product over the sum" method of calculations, which in turn reveals a startling connection to the mathematics we are developing, called the reciprocal system of mathematics.
In fact, they think any given neutrino has three very small masses, and the most popular speculation is that these masses act like a mass sitting on a seesaw with a much heavier mass! They call this "credible supposition," because "reputable" scientists are currently testing this hypothesis (see here)!
Of course, their concept of the seesawing masses is not even close to ours, since the whole LST concept is radically different than the RST concept. Yet, the very fact that they have been led to the triality of the seesaw is quite delightful. Unfortunately, however, in order to explain it, they have to resort to ill or undefined concepts such as "force," "spin," "charge" and "mass."
In the LRC's RST-based theory, our RSt, if you will, there are three and only three neutrinos and they are massless. Furthermore, they each consist of three "massless" seesaws (see previous post above,) which are "balanced" in one sense, but not in another sense.
In the sense that they are balanced, we understand it as we do the inverse of a rational number, where one rational is on the positive side of 1/1 and its inverse is on the other side, an equal distance from 1/1, but in the opposite "direction." In the other sense, however, a rational number n/1 is far from equal to its inverse. In fact, it's n2 greater than its inverse!
These differences are important to understand, in a universe of motion, which is limited to no more than three dimensions. We've seen how great this works out for the mathematics of the one-dimensional case, such as electrical charge, because two, opposite, 1d lengths are naturally understood as equal and opposite. This is not the case, however, in higher dimensions. In two dimensions, the inverse of n2 is not "equal and opposite" that of n2. It's at least 16 times smaller (22/1 ÷ 1/22 = 16), in our quantum world! In three dimensions, the difference is even more startling. The inverse of the smallest rational cubed , 23/1, is 64 times smaller than it is (23/1 ÷1/23 = 64).
Nevertheless, physical entities are not composed of discrete numbers, even though it would be a whole lot easier if they were. In our theory, the discrete numbers help define the physical entities and thus help us to understand them. This is especially helpful in understanding how the dynamics of pulsating volumes are mistaken for those of impossible rotations, treated as quantum spin. Originally, for the LST community, this quantum magnitude was thought of as an "equal but opposite" property, necessary to distinguish between two electrons sharing the same orbit around an atomic nucleus, but having no true classical interpretation that could be found to fit the requirements (this caveat is routinely mentioned in LST presentations to the lay public, with no reference to the work stoppage it should invoke. This is another instance like that of the vacuum catastrophe of quantum field theory (see here).)
In the case of the neutrinos, the concept of quantum spin is used to differentiate between observed neutrinos and something called "sterile neutrinos." These are postulated neutrinos that interact with "right-handed" particles, something which has never been observed, since observed neutrinos only interact with left-handed particles and right-handed anti-particles. The postulated neutrinos are called "sterile," because, unlike observed neutrinos, there is no known lepton particle to associate with them.
I suspect that this has to do with the nature of anti-neutrinos in the cosmic sector of the RST-based theories, but I'm not sure just how that might work yet. What's so interesting at this point is the three internal masses that the LST community feels might actually account for the observed neutrino oscillation, through the "seesaw mechanism."
This mechanism, as they call it, creates a superposition of the neutrino's internal masses, whose matter waves vary slightly, creating a beat frequency that varies with time (see here.)
The analogy used in the video linked to above, where rotating arrows are used to explain the idea of three internal neutrino masses works well, but the underlying idea that comes into play, as the seesaw mechanism, is missing. That idea coupled with the fundamental concept of quantum mechanics, the dual particle/wave nature of matter, which de Broglie first showed, the so-called matter wave, is more clearly explained in the following video, where Kenneth Long of Imperial College of London explains it here.
The seesaw bit comes into play, at the point where he says, "The neutrino is neutral, so I can try to write that as the sum of two neutral states...." These two "neutral states" are neutral in the sense of charge, but not in terms of mass, which varies, and if their masses are not equal, neither are their associated matter wavelengths, resulting in the time-varying momentum compared to that of the non time-varying momentum of the electron.
Again, the idea of dimension comes into play here, because charge is one-dimensional and thus "equal and opposite" in the seesaw analogy, but mass is three-dimensional and thus far from "equal" on the seesaw.
Of course, if there are three such internal masses, as is supposed, then one has to treat them two at a time, just like we do in calculating the current in parallel electric circuits, where we take two paths at a time, and do the product over the sum to get an effective resistance that can then be paired up with the next element and the procedure repeated as necessary to arrive at the final answer.
For those of you following the LRC's RSt in these posts, your interest will no doubt be piqued once again, as, here, the RST's universe of motion clarifies, in very simple terms, something very fundamental, which I'll try to get to next time: Larson's central idea of space/time and time/space "speed displacements" is not only germane to the current topic, but is ultimately related through this "product over the sum" method of calculations, which in turn reveals a startling connection to the mathematics we are developing, called the reciprocal system of mathematics.
Re: Meeting a Terrific Challenge
Your link does not point anywhere.
Conventional science does not recognize the charged and uncharged states of the RS, so they miss an obvious explanation of neutrino oscillation: it is nothing more than a magnetically-charged neutrino. See the 2008 post: Neutrino charge.dbundy wrote: ↑Thu Jun 21, 2018 12:05 pm I suspect that this has to do with the nature of anti-neutrinos in the cosmic sector of the RST-based theories, but I'm not sure just how that might work yet. What's so interesting at this point is the three internal masses that the LST community feels might actually account for the observed neutrino oscillation, through the "seesaw mechanism."
This mechanism, as they call it, creates a superposition of the neutrino's internal masses, whose matter waves vary slightly, creating a beat frequency that varies with time (see here.)
Every dogma has its day...
Re: Meeting a Terrific Challenge
Thanks for the heads up on the broken link, Bruce. I have fixed it. And the idea of the charged neutrino is very interesting, but the extent of the suspected neutrino mass is so small it would seem difficult to quantify it that way.
In any event, in the LRC RSt, 1d or electric charge originates in the imbalance of three S|T (T|S) units (3(2S|T) or 3(2T|S), while there is no imbalance in the theory's neutrino, because all three components have one S|T unit and one T|S unit (3(S|T) or 3(T|S)).
I'm still working on a way that the dimensional difference between the 1d electrical charge and the 3d mass "charge" might account for the oscillation, but I haven't had the time yet to think it through.
Thanks again for your input.
In any event, in the LRC RSt, 1d or electric charge originates in the imbalance of three S|T (T|S) units (3(2S|T) or 3(2T|S), while there is no imbalance in the theory's neutrino, because all three components have one S|T unit and one T|S unit (3(S|T) or 3(T|S)).
I'm still working on a way that the dimensional difference between the 1d electrical charge and the 3d mass "charge" might account for the oscillation, but I haven't had the time yet to think it through.
Thanks again for your input.
Re: Meeting a Terrific Challenge
I've said it before and I'll say it again, theoretical physics research takes courage, because you risk painting yourself into a corner and looking like a red-faced fool. 
As the search for an explanation for the origin of mass in the LRC's RSt continues, we have seen Brian Nelson's brilliant use of unit energy, the Pythagorean theorem and Einstein's and Planck's energy equations to arrive at quark masses, through numerical methods, and we've seen neutrino physics contemplate a "seesaw" concept, or reciprocal idea of internal masses in the neutrino, to explain "neutrino oscillation," where the electron, muon and tau flavors of neutrinos transform into each other, over time, as they propagate.
In our nascent theory, neutrinos don't oscillate, at least not yet, but the neutrino and the anti-neutrino are identical, except for their chirality, which is probably impossible to distinguish in any physical manner, effectively making them "Majorana" particles, in our RSt. This is very interesting, because the LST community suspects that if this is so, it would explain many mysteries of physics, including the origin of mass (see here.)
While I see many connections and tantalizing hints in all of this, the biggest problem is sorting it out in a systematic way - deducing the answers from the fundamental postulates of the RST. Our RST-based investigation has proven spectacularly successful to this point, so there's no reason to suppose it won't continue to do so.
However, the latest conclusion that we are examining, based on the consequences of the three units of measure, the square roots of 1, 2 and 3, derived from the scalar algebra and geometry of three dimensions of space/time (time/space), has led me to fear lately that I may be out on a precarious limb here.
Yet, I can see no other way to differentiate the particle families that make up our version of the standard model, with three properties that have colorless combinations of color-like characteristics to solve the spin, anti-spin, conundrum of three, fractional, "charges," assuming the Pauli exclusion principle must hold.
Not only that, but then there is the matter of the gluons and the so-called "strong force," which the LST theory postulates to explain the inelastic scattering experiments.
The basic idea is to explain how the "nucleus" of the atom, the proton with its three quarks, and the combination of protons with their positive electrical charges so tightly bound, can be kept together, when these charges oppose each other with such force, at such small radii.
Of course, its seldom mentioned, but the LST electron itself is inexplicable, and for the same reason. However, in our RSt, the problem doesn't exist, because the "charges" are understood as reciprocal motions that balance out in the atom. The electron's "charge" of 6/3 = -3 (here 3 is the unit electrical charge) and the proton's "charge" of 10/13 = 3 are combined into the Hydrogen atom's neutral "charge" of 16/16, so there is no electrostatic repulsion between protons, in the atoms of the elements.
Furthermore, there is no repulsion within the nucleons between the two like quarks either (two ups or two downs), because a dimensional factor comes into play, which prevents it.
The dimensional factor is part of our own seesaw mechanism, in that a seesaw is necessarily one-dimensional. Since each fermion in our RSt consists of a combination of three seesaws, we can assume that they each occupy independent, that is, orthogonal dimensions.
In the case of neutrinos, quarks and leptons, this is straightforward, but in the case of the combos of quarks in the nucleons, it is more subtle. How can five unbalanced seesaws (sss) and four balanced ones, nine sss altogether, be made to fit into three independent dimensions?
The way to do that, in the case of the proton, is to take one of the two up quarks, containing two 1|2 sss, one in each of two dimensions and combine it with the down quark, containing one 2|1 ss:
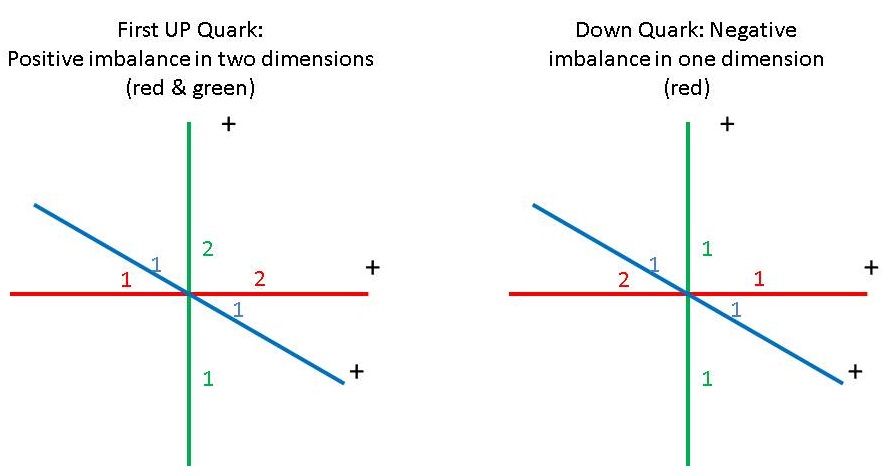
Figure 1: Dimensional Distribution of Up Quark and Down Quark S|T Units
When combined with this up quark, the down quark will balance out one of the up quark's two unbalanced dimensions: 2|1 + 1|2 = 3|3. This effectively leaves two dimensions balanced and one dimension unbalanced in the quark combo, making it possible to add a second up quark to the combo in these two balanced dimensions:
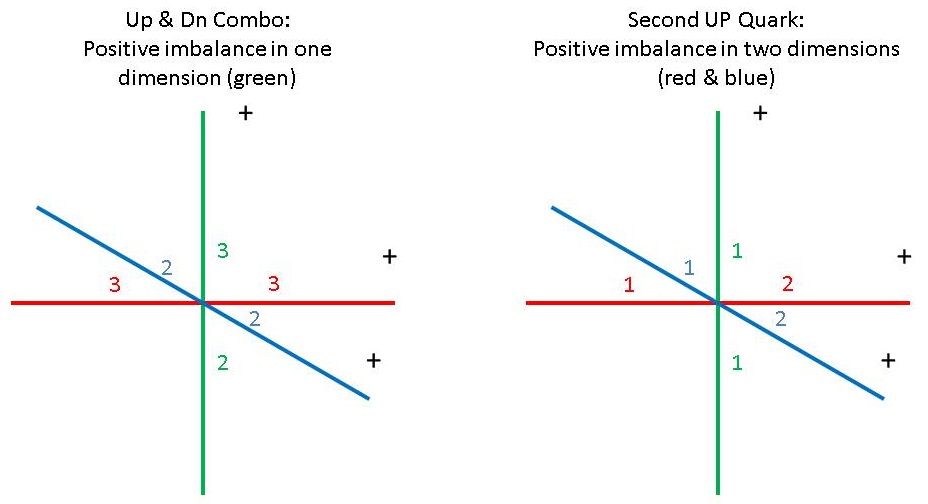
Figure 2. Left: The Quark Combo. Right: The Second Up Quark
Combining this combo, with two balanced dimensions, with the second up quark, with two unbalanced dimensions, results in three unbalanced dimensions, of one positive unit each, and, like in the electron, the fact that each of the three total units exists in an orthogonal, or independent dimension means there can be no repulsion force between them:
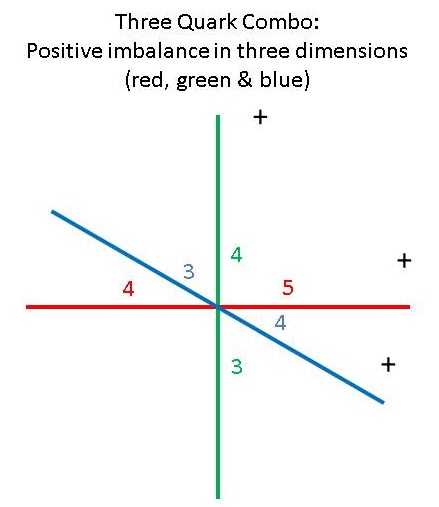
Figure 3: The Proton's Three Quark Combo with Three Positively Charged Dimensions
Again, the dimensions are independent, so no repulsion force is generated between them, but the magnitude in one dimension differs from the others, because of the balancing act of the down quark in the 3|3 dimension. In that dimension the imbalance is the same as in the other dimensions (one unit), but the ss magnitude is 4|5, instead of 3|4, as in the other two dimensions.
The colors of the dimensions in the above graphics are meant to distinguish the three dimensions. They are not related to the LST's idea of "color charges." However, that idea is there too, as the three quarks are unbalanced in three unique dimensions, or set of dimensions: either 1&2 or 1&3 or 2&3 for the up quarks, and 3 or 2 or 1, for the down quark, depending on which configuration the up quarks take.
Of course, we can do the same thing with the three quarks of the neutron, but in that case, one dimension of lesser magnitude rather than greater emerges from the combo, and, as already noted, in the case of the electron, each of the three dimensions is unbalanced, so it repels other electrons and same goes for two positrons. In every case, there is no internal repulsion of like charges to overcome, because they reside in independent dimensions, but they do repulse like charges that are external to them.
Consequently, the F = qq'/r2 equation doesn't even apply in the case of the quark combos, and this means that there is no need for an autonomous "strong force" to overcome it, and there is no need of its supposed carrier particle, the gluon, to explain the stability of nucleons and combinations of nucleons, as atomic elements and their isotopes, either.
However, there's still the matter of the quantum spin states. If no two identical spin states can coexist in the quarks of nucleons, then the quantum spins of three quarks have to be incompatible, all else being equal, since two of the three would have to be the same (two up or two down states in the quantum theory of the LST).
Consequently, the LST community has also invented the color force property to deal with this problem. As long as each of the three constituent quarks of a nucleon has a unique one of these three primary "color charges," all three of their spin states can be identical and it makes no difference to the calculations of the theory (see here.)
It's worth noting, however, that they admit in this video that proving that these color charges actually exist is "tricky," but without them, they can't make sense of their experimental data.
However, in our model, it's easy to see, as I have just shown above, how the three quarks differ in their dimensional characteristics, in a three "color" set-like way. What makes this so interesting is that the gluons of their theory, that is the carriers of the color charge, come in eight different versions. This is because, for the theory to work, the gluons, even though they are bosons, as are photons, are nevertheless "charged" bosons, unlike photons. They are charged with the color charge and so there arises a color charge dynamic between them, further complicating their picture of physical reality.
Now, given that our theory has no need for autonomous forces, let alone one like the strong nuclear force, and thus no need of gluons, the fact remains that the LST can account for empirical observations, using these ad hoc concepts. This drives me to try to understand what it's all about and why David Gross et. al, received a Nobel Prize in theoretical physics, for coming up with it.
In their theory, the gluons actually carry a combination of color charge and anti-color charge, so, since there are three each of these, that would normally make you think that there should be 3 x 3 = 9, distinct gluons, but there aren't! There are only eight distinct gluons and the reason has to do with three dimensions!
How interesting is it that, given that the three integer values of our three unit sizes (square root of 1, 2 and 3) of the S|T (T|S) oscillations making up our motion combos (see post on this above), are due to the fundamental concepts of two "directions" in three dimensions and 23 = 8?
The only way I could see to tie different color-like properties that fit together like primary "colors," neutralizing the combo, was to use our three units as the radii of three sets of oscillations, each of which has three associated oscillations, in which the radius of one and only one is a unique integer magnitude (1, 2 or 3). The integer 1 is associated with the 1d element of the first set (√((√1)2+(√0)2+(√0)2)); the integer 2 is associated with the 2d element of the second set (√((√2)2+(√2)2+(√0)2)); and the integer 3 is associated with the 3d element of the third set (√((√3)2+(√3)2+(√3)2)).
Though I hoped it would be, I had no idea at the time that the gluon concept of the LST's theory of quantumchromodynamics (QCD) was also based on the dimensional properties of these "charges," but so it turns out to be: One Internet commentator answered the question, why there are only 8 gluons, as follows:
“Quarks transform under this representation of SU(3), and because it's 3-dimensional we say quarks come in 3 colors: red, green and blue.” Since the matrices must have zero trace, the number of independent possibilities is cut to 8."
This is the most succinct statement I could find of this fact, but if you are interested in more detail, our old friend John Baez has explained it here. For those that don't mind computer voices, there's less math and more graphics here.
The bottom line is I can't put it all together yet, but there are enough clues coming in that I feel really positive that we can eventually get there - or not. I may be painting myself into a corner with the color "foolishness." Ha!
As the search for an explanation for the origin of mass in the LRC's RSt continues, we have seen Brian Nelson's brilliant use of unit energy, the Pythagorean theorem and Einstein's and Planck's energy equations to arrive at quark masses, through numerical methods, and we've seen neutrino physics contemplate a "seesaw" concept, or reciprocal idea of internal masses in the neutrino, to explain "neutrino oscillation," where the electron, muon and tau flavors of neutrinos transform into each other, over time, as they propagate.
In our nascent theory, neutrinos don't oscillate, at least not yet, but the neutrino and the anti-neutrino are identical, except for their chirality, which is probably impossible to distinguish in any physical manner, effectively making them "Majorana" particles, in our RSt. This is very interesting, because the LST community suspects that if this is so, it would explain many mysteries of physics, including the origin of mass (see here.)
While I see many connections and tantalizing hints in all of this, the biggest problem is sorting it out in a systematic way - deducing the answers from the fundamental postulates of the RST. Our RST-based investigation has proven spectacularly successful to this point, so there's no reason to suppose it won't continue to do so.
However, the latest conclusion that we are examining, based on the consequences of the three units of measure, the square roots of 1, 2 and 3, derived from the scalar algebra and geometry of three dimensions of space/time (time/space), has led me to fear lately that I may be out on a precarious limb here.
Yet, I can see no other way to differentiate the particle families that make up our version of the standard model, with three properties that have colorless combinations of color-like characteristics to solve the spin, anti-spin, conundrum of three, fractional, "charges," assuming the Pauli exclusion principle must hold.
Not only that, but then there is the matter of the gluons and the so-called "strong force," which the LST theory postulates to explain the inelastic scattering experiments.
The basic idea is to explain how the "nucleus" of the atom, the proton with its three quarks, and the combination of protons with their positive electrical charges so tightly bound, can be kept together, when these charges oppose each other with such force, at such small radii.
Of course, its seldom mentioned, but the LST electron itself is inexplicable, and for the same reason. However, in our RSt, the problem doesn't exist, because the "charges" are understood as reciprocal motions that balance out in the atom. The electron's "charge" of 6/3 = -3 (here 3 is the unit electrical charge) and the proton's "charge" of 10/13 = 3 are combined into the Hydrogen atom's neutral "charge" of 16/16, so there is no electrostatic repulsion between protons, in the atoms of the elements.
Furthermore, there is no repulsion within the nucleons between the two like quarks either (two ups or two downs), because a dimensional factor comes into play, which prevents it.
The dimensional factor is part of our own seesaw mechanism, in that a seesaw is necessarily one-dimensional. Since each fermion in our RSt consists of a combination of three seesaws, we can assume that they each occupy independent, that is, orthogonal dimensions.
In the case of neutrinos, quarks and leptons, this is straightforward, but in the case of the combos of quarks in the nucleons, it is more subtle. How can five unbalanced seesaws (sss) and four balanced ones, nine sss altogether, be made to fit into three independent dimensions?
The way to do that, in the case of the proton, is to take one of the two up quarks, containing two 1|2 sss, one in each of two dimensions and combine it with the down quark, containing one 2|1 ss:
Figure 1: Dimensional Distribution of Up Quark and Down Quark S|T Units
When combined with this up quark, the down quark will balance out one of the up quark's two unbalanced dimensions: 2|1 + 1|2 = 3|3. This effectively leaves two dimensions balanced and one dimension unbalanced in the quark combo, making it possible to add a second up quark to the combo in these two balanced dimensions:
Figure 2. Left: The Quark Combo. Right: The Second Up Quark
Combining this combo, with two balanced dimensions, with the second up quark, with two unbalanced dimensions, results in three unbalanced dimensions, of one positive unit each, and, like in the electron, the fact that each of the three total units exists in an orthogonal, or independent dimension means there can be no repulsion force between them:
Figure 3: The Proton's Three Quark Combo with Three Positively Charged Dimensions
Again, the dimensions are independent, so no repulsion force is generated between them, but the magnitude in one dimension differs from the others, because of the balancing act of the down quark in the 3|3 dimension. In that dimension the imbalance is the same as in the other dimensions (one unit), but the ss magnitude is 4|5, instead of 3|4, as in the other two dimensions.
The colors of the dimensions in the above graphics are meant to distinguish the three dimensions. They are not related to the LST's idea of "color charges." However, that idea is there too, as the three quarks are unbalanced in three unique dimensions, or set of dimensions: either 1&2 or 1&3 or 2&3 for the up quarks, and 3 or 2 or 1, for the down quark, depending on which configuration the up quarks take.
Of course, we can do the same thing with the three quarks of the neutron, but in that case, one dimension of lesser magnitude rather than greater emerges from the combo, and, as already noted, in the case of the electron, each of the three dimensions is unbalanced, so it repels other electrons and same goes for two positrons. In every case, there is no internal repulsion of like charges to overcome, because they reside in independent dimensions, but they do repulse like charges that are external to them.
Consequently, the F = qq'/r2 equation doesn't even apply in the case of the quark combos, and this means that there is no need for an autonomous "strong force" to overcome it, and there is no need of its supposed carrier particle, the gluon, to explain the stability of nucleons and combinations of nucleons, as atomic elements and their isotopes, either.
However, there's still the matter of the quantum spin states. If no two identical spin states can coexist in the quarks of nucleons, then the quantum spins of three quarks have to be incompatible, all else being equal, since two of the three would have to be the same (two up or two down states in the quantum theory of the LST).
Consequently, the LST community has also invented the color force property to deal with this problem. As long as each of the three constituent quarks of a nucleon has a unique one of these three primary "color charges," all three of their spin states can be identical and it makes no difference to the calculations of the theory (see here.)
It's worth noting, however, that they admit in this video that proving that these color charges actually exist is "tricky," but without them, they can't make sense of their experimental data.
However, in our model, it's easy to see, as I have just shown above, how the three quarks differ in their dimensional characteristics, in a three "color" set-like way. What makes this so interesting is that the gluons of their theory, that is the carriers of the color charge, come in eight different versions. This is because, for the theory to work, the gluons, even though they are bosons, as are photons, are nevertheless "charged" bosons, unlike photons. They are charged with the color charge and so there arises a color charge dynamic between them, further complicating their picture of physical reality.
Now, given that our theory has no need for autonomous forces, let alone one like the strong nuclear force, and thus no need of gluons, the fact remains that the LST can account for empirical observations, using these ad hoc concepts. This drives me to try to understand what it's all about and why David Gross et. al, received a Nobel Prize in theoretical physics, for coming up with it.
In their theory, the gluons actually carry a combination of color charge and anti-color charge, so, since there are three each of these, that would normally make you think that there should be 3 x 3 = 9, distinct gluons, but there aren't! There are only eight distinct gluons and the reason has to do with three dimensions!
How interesting is it that, given that the three integer values of our three unit sizes (square root of 1, 2 and 3) of the S|T (T|S) oscillations making up our motion combos (see post on this above), are due to the fundamental concepts of two "directions" in three dimensions and 23 = 8?
The only way I could see to tie different color-like properties that fit together like primary "colors," neutralizing the combo, was to use our three units as the radii of three sets of oscillations, each of which has three associated oscillations, in which the radius of one and only one is a unique integer magnitude (1, 2 or 3). The integer 1 is associated with the 1d element of the first set (√((√1)2+(√0)2+(√0)2)); the integer 2 is associated with the 2d element of the second set (√((√2)2+(√2)2+(√0)2)); and the integer 3 is associated with the 3d element of the third set (√((√3)2+(√3)2+(√3)2)).
Though I hoped it would be, I had no idea at the time that the gluon concept of the LST's theory of quantumchromodynamics (QCD) was also based on the dimensional properties of these "charges," but so it turns out to be: One Internet commentator answered the question, why there are only 8 gluons, as follows:
“Quarks transform under this representation of SU(3), and because it's 3-dimensional we say quarks come in 3 colors: red, green and blue.” Since the matrices must have zero trace, the number of independent possibilities is cut to 8."
This is the most succinct statement I could find of this fact, but if you are interested in more detail, our old friend John Baez has explained it here. For those that don't mind computer voices, there's less math and more graphics here.
The bottom line is I can't put it all together yet, but there are enough clues coming in that I feel really positive that we can eventually get there - or not. I may be painting myself into a corner with the color "foolishness." Ha!
Re: Meeting a Terrific Challenge
In the previous post above, the so-called "color charge" of the strong nuclear force, in the LST's standard model of particle physics, was shown not to exist in the model of the LRC's RSt.
However, our RSt model does contain a dimensional phenomena that acts in the same way the LST's "color charge" does, in that it requires each constituent quark of a nucleon to be unique in a dimensional sense that can be compared to the relation of three primary colors mixing to white, a colorless or neutral state.
Unfortunately, I didn't show how these dimensional "colors" work in the above post, so I would like to do that now. In the graphic below, the three dimensions are numbered, and unique sets of references to two of them are colored red, blue and green. These are the three possibilities of assigning dimensions to the quarks, where each up quark has two positively unbalanced S|T units (blue middle dots) and one balanced one (green middle dot):

Representing this quark on the three orthogonal axes, requires us to choose two to be the unbalanced dimensions (seesaws), leaving one balanced. This gives us three colored sets of unbalanced up quark axes to choose from, as shown in the graphic below.
Now, the down quark only has one negative unbalanced S|T unit (red middle dot) and two balanced (green) ones:

Consequently, this one unbalanced unit can align in any of the three dimensions, and these are listed in the graphic, as the colored numbers, 2, 1 and 3.
We need to have three dimensions that are unbalanced by one positive unit for a total of +3 for the proton, so first we choose a colored set, say red, for the first up quark. This red set has the two positively unbalanced S|T units in axes 1 and 2 and the balanced one is in axis 3. So, picking a down quark to balance one of the unbalanced positive units of the up quark, we pick the blue 2 down quark, to balance out axis 2 of the red up quark. So, now we have two of the three primary color quarks.
As a result, the positive and negative units in axis 2 of the combo now balance, providing two balanced axes for the second up quark to fit into (that is axes 2 and 3 of the nucleon are now balanced), and we can now add the green up quark to the combo, with positive unbalance in axes 2&3, giving us a total of three unbalanced axes in the combo, since axis 1 of the red up quark is also unbalanced and unchanged by the addition of the green up quark, with a balanced axis 1. Therefore, we now have the three "colors" we need for the quark combination of the proton, with three unbalanced dimensions, for a total of 3 positive charges.
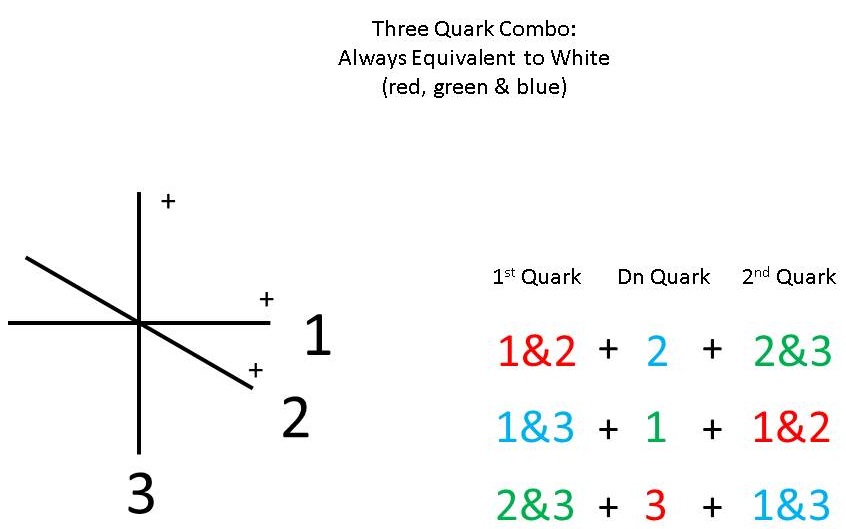
The alternative choices follow, in the same manner. In the second instance, the negative unit of axis 1 of the green down quark balances out the positive unit in axis 1 of the blue up quark, leaving its axis 3 unbalanced. Adding a red up quark to the combo, unbalanced in axes 1&2, again gives it a total of three unbalanced axes. In the third case, axis 3 of the green up quark is balanced by the red down quark, and adding the blue up quark gives the combo three unbalanced axes in total.
In each case, the combo of red, blue and green quarks is a colorless combination.
However, our RSt model does contain a dimensional phenomena that acts in the same way the LST's "color charge" does, in that it requires each constituent quark of a nucleon to be unique in a dimensional sense that can be compared to the relation of three primary colors mixing to white, a colorless or neutral state.
Unfortunately, I didn't show how these dimensional "colors" work in the above post, so I would like to do that now. In the graphic below, the three dimensions are numbered, and unique sets of references to two of them are colored red, blue and green. These are the three possibilities of assigning dimensions to the quarks, where each up quark has two positively unbalanced S|T units (blue middle dots) and one balanced one (green middle dot):

Representing this quark on the three orthogonal axes, requires us to choose two to be the unbalanced dimensions (seesaws), leaving one balanced. This gives us three colored sets of unbalanced up quark axes to choose from, as shown in the graphic below.
Now, the down quark only has one negative unbalanced S|T unit (red middle dot) and two balanced (green) ones:

Consequently, this one unbalanced unit can align in any of the three dimensions, and these are listed in the graphic, as the colored numbers, 2, 1 and 3.
We need to have three dimensions that are unbalanced by one positive unit for a total of +3 for the proton, so first we choose a colored set, say red, for the first up quark. This red set has the two positively unbalanced S|T units in axes 1 and 2 and the balanced one is in axis 3. So, picking a down quark to balance one of the unbalanced positive units of the up quark, we pick the blue 2 down quark, to balance out axis 2 of the red up quark. So, now we have two of the three primary color quarks.
As a result, the positive and negative units in axis 2 of the combo now balance, providing two balanced axes for the second up quark to fit into (that is axes 2 and 3 of the nucleon are now balanced), and we can now add the green up quark to the combo, with positive unbalance in axes 2&3, giving us a total of three unbalanced axes in the combo, since axis 1 of the red up quark is also unbalanced and unchanged by the addition of the green up quark, with a balanced axis 1. Therefore, we now have the three "colors" we need for the quark combination of the proton, with three unbalanced dimensions, for a total of 3 positive charges.

The alternative choices follow, in the same manner. In the second instance, the negative unit of axis 1 of the green down quark balances out the positive unit in axis 1 of the blue up quark, leaving its axis 3 unbalanced. Adding a red up quark to the combo, unbalanced in axes 1&2, again gives it a total of three unbalanced axes. In the third case, axis 3 of the green up quark is balanced by the red down quark, and adding the blue up quark gives the combo three unbalanced axes in total.
In each case, the combo of red, blue and green quarks is a colorless combination.
Re: Meeting a Terrific Challenge
I've been watching a six hour set of YouTube videos featuring Sean Carroll called "The Higgs Boson and Beyond." Wow, is it ever good. Great lecturer, super graphics and lots of non-mathematical detail in historical context.
It's helped me fill in lots of gaps in my understanding of the LST's development, and I'm only half-way through it. The trouble is, it makes me miserable as I see so many ways the LST's limited concept of motion and mathematics has forced them into complicated and tortuous solutions that would otherwise be quite simple and straightforward, if they were blessed with Larson's insight, as we are.
These people are really smart, but sometimes Sean's attitude seems a bit arrogant and over-confident, given the perspective of the RST community. We are so completely enamored with Larson's beautiful system of physical theory that the ideas of quantum fields, permeating all "space" and autonomous, spirit-like, forces and apparent ignorance of space/time (time/space) dimensions and much more, causes me, at least, to chaff, as I listen to complicated and difficult to grasp concepts of gauges and symmetry and gradients, etc, in connection with mass and spin and energy, and whatnot.
I suffer the pain, though, because I want to understand the Higgs boson, the Higgs field and the Higgs mechanism, since it's so highly regarded by them and they have been hoping to find it for so long and now that they think they have found it, at least the boson, you have to give them credit. But still...
The fact that, in their theory, the Higgs has 0 spin, but lots of energy and that fermions and leptons have spin, but no mass, except what they get by coupling with the Higgs field, tempts me to compare their Higgs with our unit progression, which has no spin, of course, but is also the origin of all mass (and charge and force and all else).
How would it be, if we could reach them and sit there in Sean's office at Cal Tech, and share with him over Feynman's desk, the conversation that the former university classmate of Larson's, Linus Pauling, the double winner of the Nobel Prize, had with Dewey, and discuss their ensuing correspondence on theoretical physics.
What Larson had to share with Pauling was truly revolutionary, but the Cal Tech professor was too much a member of the good old boys club of famous physicists, at that point in time, to care much about the discovery of his long-time friend, with whom he once shared a much more humble award.
Quantum mechanics was all the rage back then, even before Feynman and QED was well-known, let alone QCD and the standard model and now the Higgs business. How exasperated Larson must have felt, in the face of such disparity. The contrast of the much touted success of quantum mechanics and the tremendous world-wide resources dedicated to its development, with the tap, tap, tap of a solitary Royal typewriter, in Larson's home office, refuting it all, couldn't have been greater.
It's fun to imagine, though, what would have happened, if Larson had deduced the 3d space/time (time/space) oscillations to begin with, instead of the 1d vibration route of theoretical development he actually followed. Had he come up with what was to become the set of standard model particles, way before they were discovered, what would have happened? What would Pauling's reaction have been then? Would he have invited Larson to give a lecture at Cal Tech, recommending him and his new system of theory to his colleagues? Would the world's scientific community have turned to investigating scalar physics and scalar mathematics, and would they have awarded him a Nobel Prize for physics? To some, it is definitely laughable to think so, but look at what he would have been able to predict:
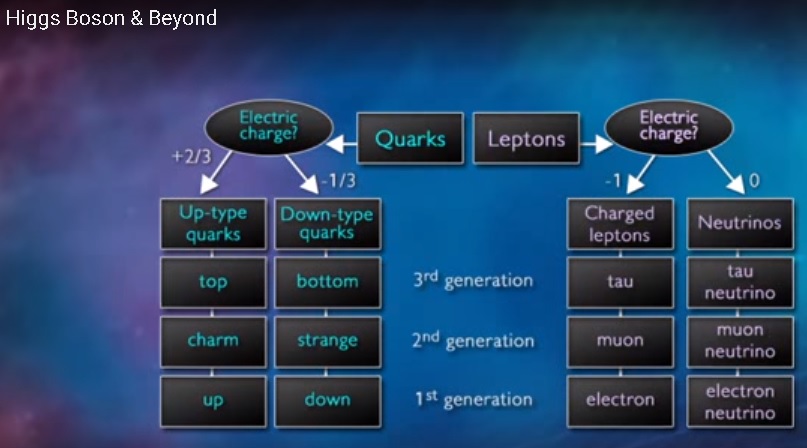
Admittedly, the content would have been interpreted differently. Larson's model of the atom is completely different. It's certainly not this:
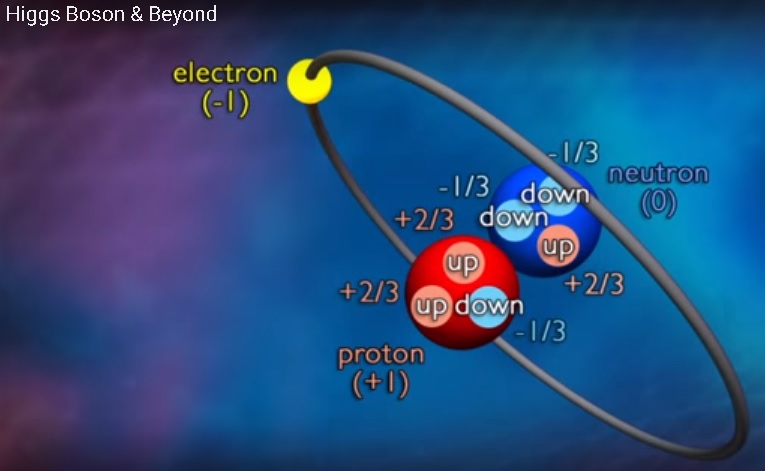
No, his argument in The Case Against the Nuclear Atom, is that the electron does not maintain its identity, orbiting the nucleus of the atom, but becomes absorbed by the proton, part and parcel, effectively neutralizing the two charges as a whole. His argument was bolstered by his attack on the electrical theory of solid cohesion, showing glaring inconsistencies that his critics were slow to refute. His conclusion was that:
"The inability of the electrical theory to furnish a consistent and comprehensive explanation of the cohesion of solids, together with the absence of any valid evidence of the existence of ions in the solid state, indicates that it will be necessary to abandon this theory as a whole, along with the concept of the nuclear atom."
However, if Larson's criticisms of the electrical theory are ignored, because the theory is all that is needed for present purposes, then it won't be abandoned and neither will the theory of the nuclear atom, and, as far as I can tell, neither one has been:
Here is one of many YouTube videos showing that fact.
Sean makes the point that the search for the Higgs was so important that the LST community spent nine billion dollars to find that little bump on the graph, but the whole truth is that the cost of not abandoning the electrical theory of solid cohesion and not abandoning the nuclear theory of the atom, as Larson suggested with his little typewriter, has cost the world orders of magnitude more than that.
In the RST, everything starts with the unit progression of space and time. There is no all pervasive field throughout space, because what is defined as space, a set of points that satisfies the postulates of geometry, does not exist until a set of points exists and sets of points, lines, areas and volumes arise from instantiation of deviations from the unity of the unit progression.
Once these deviations are instantiated, either as a positive deviation or a negative one, they can be combined in equal numbers or unequal numbers, in two different ways. If unequal, the number of one is greater or lesser than the number of the other, and combining these equalities and inequalities, in the two ways they may be combined, results in a set of building blocks that can be employed to construct the observed universe.
So, in a sense, we can agree with the LST that a "god particle" is needed to begin with, only we call it a space/time (time/space) deviation from unit progression, rather than the spontaneously broken symmetry of an all pervasive field, and it doesn't take an expensive machine to find it either, or at least the symmetry from which it derives. It only takes a modest telescope and a clock to see that.
Maybe we should call it the "Larson boson," but then, again, he wasn't exactly a "boson," was he?
It's helped me fill in lots of gaps in my understanding of the LST's development, and I'm only half-way through it. The trouble is, it makes me miserable as I see so many ways the LST's limited concept of motion and mathematics has forced them into complicated and tortuous solutions that would otherwise be quite simple and straightforward, if they were blessed with Larson's insight, as we are.
These people are really smart, but sometimes Sean's attitude seems a bit arrogant and over-confident, given the perspective of the RST community. We are so completely enamored with Larson's beautiful system of physical theory that the ideas of quantum fields, permeating all "space" and autonomous, spirit-like, forces and apparent ignorance of space/time (time/space) dimensions and much more, causes me, at least, to chaff, as I listen to complicated and difficult to grasp concepts of gauges and symmetry and gradients, etc, in connection with mass and spin and energy, and whatnot.
I suffer the pain, though, because I want to understand the Higgs boson, the Higgs field and the Higgs mechanism, since it's so highly regarded by them and they have been hoping to find it for so long and now that they think they have found it, at least the boson, you have to give them credit. But still...
The fact that, in their theory, the Higgs has 0 spin, but lots of energy and that fermions and leptons have spin, but no mass, except what they get by coupling with the Higgs field, tempts me to compare their Higgs with our unit progression, which has no spin, of course, but is also the origin of all mass (and charge and force and all else).
How would it be, if we could reach them and sit there in Sean's office at Cal Tech, and share with him over Feynman's desk, the conversation that the former university classmate of Larson's, Linus Pauling, the double winner of the Nobel Prize, had with Dewey, and discuss their ensuing correspondence on theoretical physics.
What Larson had to share with Pauling was truly revolutionary, but the Cal Tech professor was too much a member of the good old boys club of famous physicists, at that point in time, to care much about the discovery of his long-time friend, with whom he once shared a much more humble award.
Quantum mechanics was all the rage back then, even before Feynman and QED was well-known, let alone QCD and the standard model and now the Higgs business. How exasperated Larson must have felt, in the face of such disparity. The contrast of the much touted success of quantum mechanics and the tremendous world-wide resources dedicated to its development, with the tap, tap, tap of a solitary Royal typewriter, in Larson's home office, refuting it all, couldn't have been greater.
It's fun to imagine, though, what would have happened, if Larson had deduced the 3d space/time (time/space) oscillations to begin with, instead of the 1d vibration route of theoretical development he actually followed. Had he come up with what was to become the set of standard model particles, way before they were discovered, what would have happened? What would Pauling's reaction have been then? Would he have invited Larson to give a lecture at Cal Tech, recommending him and his new system of theory to his colleagues? Would the world's scientific community have turned to investigating scalar physics and scalar mathematics, and would they have awarded him a Nobel Prize for physics? To some, it is definitely laughable to think so, but look at what he would have been able to predict:

Admittedly, the content would have been interpreted differently. Larson's model of the atom is completely different. It's certainly not this:

No, his argument in The Case Against the Nuclear Atom, is that the electron does not maintain its identity, orbiting the nucleus of the atom, but becomes absorbed by the proton, part and parcel, effectively neutralizing the two charges as a whole. His argument was bolstered by his attack on the electrical theory of solid cohesion, showing glaring inconsistencies that his critics were slow to refute. His conclusion was that:
"The inability of the electrical theory to furnish a consistent and comprehensive explanation of the cohesion of solids, together with the absence of any valid evidence of the existence of ions in the solid state, indicates that it will be necessary to abandon this theory as a whole, along with the concept of the nuclear atom."
However, if Larson's criticisms of the electrical theory are ignored, because the theory is all that is needed for present purposes, then it won't be abandoned and neither will the theory of the nuclear atom, and, as far as I can tell, neither one has been:
Here is one of many YouTube videos showing that fact.
Sean makes the point that the search for the Higgs was so important that the LST community spent nine billion dollars to find that little bump on the graph, but the whole truth is that the cost of not abandoning the electrical theory of solid cohesion and not abandoning the nuclear theory of the atom, as Larson suggested with his little typewriter, has cost the world orders of magnitude more than that.
In the RST, everything starts with the unit progression of space and time. There is no all pervasive field throughout space, because what is defined as space, a set of points that satisfies the postulates of geometry, does not exist until a set of points exists and sets of points, lines, areas and volumes arise from instantiation of deviations from the unity of the unit progression.
Once these deviations are instantiated, either as a positive deviation or a negative one, they can be combined in equal numbers or unequal numbers, in two different ways. If unequal, the number of one is greater or lesser than the number of the other, and combining these equalities and inequalities, in the two ways they may be combined, results in a set of building blocks that can be employed to construct the observed universe.
So, in a sense, we can agree with the LST that a "god particle" is needed to begin with, only we call it a space/time (time/space) deviation from unit progression, rather than the spontaneously broken symmetry of an all pervasive field, and it doesn't take an expensive machine to find it either, or at least the symmetry from which it derives. It only takes a modest telescope and a clock to see that.
Maybe we should call it the "Larson boson," but then, again, he wasn't exactly a "boson," was he?
Re: Meeting a Terrific Challenge
The Higgs Boson was identified in RS2 back in 2012 as nothing more than the cosmic rotational base. See: Higgs Boson.dbundy wrote: ↑Mon Jul 09, 2018 2:47 pm I suffer the pain, though, because I want to understand the Higgs boson, the Higgs field and the Higgs mechanism, since it's so highly regarded by them and they have been hoping to find it for so long and now that they think they have found it, at least the boson, you have to give them credit.
If you accept Larson's premise that everything begins with a photon (a direction reversal), then the Higgs Boson is an impossible structure in the RS because the photon is spin-1 and therefore all motion compounded on it will have a non-zero spin.
There is only ONE condition of motion that exists with a spin-0, the one that Larson skipped and Nehru introduced: the angular progression of the natural reference system (the yin aspect). Because progression (both linear and angular forms) has no displacement, it cannot have spin, therefore, spin-0. Linear motion does not have the appearance of particles, but angular motion (Larson's scalar rotation) does. The reason the Higgs Boson is so elusive is that it has no displacement--and therefore cannot interact with anything in either space or time.
Every dogma has its day...