The shift in the scientific paradigm, from a system of theory, which posits matter in a framework of space and time, and seeks to reduce it to the fewest number of interactions between the fewest number of particles, to a system of theory, which posits nothing but motion, in three dimensions, existing in discrete units, with two reciprocal aspects, space and time, requires a significant shift in mathematics as well.
I know Larson didn't think so, but it's true. The entire foundation of the Newtonian program of research is based on his laws of motion and the algebra that developed along with them, culminating in Maxwell's equations, as reformulated by Gibbs and Heaviside. Thus, the equations of velocity, mass and energy enabled the construction of more and more useful and efficacious physical models, based on what came to be known as vector algebra.
For example, the simple equation of velocity, v = Δs/Δt, enabled the modeling of vector motion, the one-dimensional motion of an object in a given direction specified in a three-dimensional coordinate system. Given the mass of the object in motion, and the velocity, v, the momentum of the object, p, could be determined, and even the kinetic energy, E = 1/2 mv2.
Of course, this was just the "begeen of the begeen." Much, much more would follow from these simple equations, until only the most trained specialist could understand them, but when it came to modeling the Hydrogen atom, it was the simple equations of velocity, acceleration, energy, mass and momentum that enabled the Bohr model.
Today, it's being recognized more and more that it's the model of the Hydrogen atom, as it has evolved, which is the root cause of the trouble with physics. The most iconoclastic assault on it is being led by Randell Mills, but, while Mills is dismantling the scaffolding of Quantum Mechanics, his new model is built on the same foundation of velocity, acceleration, momentum, mass, energy, etc.
In other words, even though Larson and Xavier Borg have independently shown that all physical units are ultimately units of space and time, the physicists of the legacy system of theory (LST) continue to ignore that astounding and game-changing fact, and its far-reaching implications.
That leaves us peons to carry on as best we can. New bottles for new wine, as they say. In this discussion of the LRC Research, based on Larson's Reciprocal System of Physical Theory (RST), I'm trying to explain how we might construct a new RST-based model of the atomic elements.
Larson made the case against the nuclear atom (here), in which he flatly rejected the planetary analogy of the Bohr model. His model, based on scalar motion, has no nucleus of small positive charge, surrounded by electrons in orbit, or in clouds, or in shells. In his model, the electron combines with the proton, both of which are combinations of scalar motion, to form a greater combination of motion,
The atomic elements were simply greater and greater combinations of scalar motion. At the LRC, we've modified Larson's assumptions of how these combinations form, and from that has emerged the building blocks of matter and radiation. We are happy that it has worked thus far, but it's only a start. The biggest challenge we face now is how to forge ahead in terms of scalar motion equations. We need equations to build sophisticated models that are as predictive as the models of Mills, which we can't use, because of fundamental confusion of physical dimensions and terms.
Terms such as Bohr radius, Planck's constant, mass, charge and energy, have been adopted by students of the RST for years, as the language of the new system, but these are all based on LST concepts of vector motion, not scalar motion. They cannot be used in equations of scalar motion to model a combination of scalar motions!
The basic combinations of the LRC's RST-based theory (RSt), work out well for one-dimensional units of "charge," because the relations between the combinations is additive, but to go beyond the one-dimensional properties of the combos, we face a great language barrier.
The LST uses units of mass, which have the 3D dimensions of the cosmic sector (cs), not because material sector (ms) motion combinations are 3D combinations of cs motion, but because mass is a concept of measuring the resistance of the combos to vector motion (inertia). The LST uses units of energy, which have the 1D dimensions of cs motion, not because energy is cs motion, but because it expresses the amount of work required to move mass in a given direction of the reference system.
Then we have units of momentum, which have the 2D dimensions of the cs, not because it is 2D cs motion, but because it is a measure of mass in vector motion, mass that is measured in terms of its resistance to motion combos in the ms!
To make matters worse, the RSt combos of motion are not just made up of combinations of ms or cs scalar motions, but an equal, or unequal, balance of both, like a bank balance sheet, in three dimensions!
The challenge is terrific, but starting with the next post, I'll share a possible approach to formulating a whole new language, suitable for our research, for what it's worth.
Meeting a Terrific Challenge
Moderator: dbundy
Re: Meeting a Terrific Challenge
If only Larson and Xavior Borg were collaborators! Imagine what they could accomplish together! Larson postulated the fundamental relation between space and time that defines an entirely new cosmology, while Borg untangled the historical units of physical measurement that have confused the work of theoretical physicists of the LST for so long, and he did it by recognizing that they can all be reduced to space and time terms.
Recall, that Borg's clarification of the SI system of units, shows that mass, in units of kilograms, a central unit of the SI system of measurement units, is, after all, "a fictitious unit."

His analysis of the SI mass unit and others is fascinating (see here), if unacknowledged by the greater LST community. Of course, these things take time, lots of it, so it may be centuries before he is given the credit he is due in the LST community.
Yet, there is no reason why the RST community should take so long. I didn't know Larson personally, unfortunately, but I'm pretty sure he would have embraced Borg's work wholeheartedly, because the work of the two men fits together so well. Though Borg's work doesn't go so far as to recognize scalar motion and the fundamental implications of the reciprocal nature of space and time, he does recognize their fundamental nature in the physical realm of the LST, which is limited to the material system of the RST.
Borg re-draws the SI diagram shown above to show that, because the space and time units are the only ones that are truly independent, they are the fundamental units in the system, when it's correctly understood:

With this as his starting point, he goes on to show how all physical units and relations between them can be expressed in space and time terms, and gives the procedure for converting the LST dimensions of any formula into what he calls ST dimensions. This is so useful to RST research that it is hard to express the magnitude of it adequately, but it comes down to the value of his insight into the ratio of the natural units of space and time to their conventional units, even though he doesn't recognize the fundamental relation of space and time as scalar motion, as did Larson.
Years ago, I took the liberty to illustrate this simple but vital difference between the work of the two men by modifying Borg's modification of the SI diagram, shown above, to one showing the units from Larson's point of view of fundamental scalar motion:
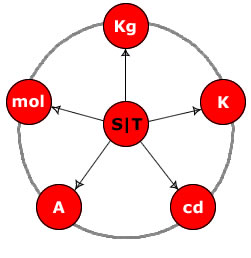
Students of the RST no doubt delight in the simplicity of the above diagram, but what's more, they realize that it is only the material sector (ms) diagram of physical units. For the cosmic sector (cs), the fundamental units of space and time are inverted, so that the unit of cs scalar motion, T/S, replaces the S/T unit, in the center of the cs version of the diagram (not shown).
How huge is this? It's almost unfathomable. It means that there is a heretofore unknown sector, an inverse sector, to the physical universe, and those of us who are familiar with Larson's works know what marvelous insight into physical phenomena that knowledge provides.
Yet, understanding that revolutionary view of the reciprocal nature of space and time and its tremendous power of clarification of the physical situation does not mean that we can use that power better than the LST community can use their view, which the brightest minds of the world have studied for centuries, regardless of how confusing we now see it is.
For sure, Larson and Borg may have argued over aspects of this situation, but I think both men would have stood their ground in certain areas, and one of those areas where Borg would have prevailed is in the conversion of conventional units to the natural units of space and time.
Larson's procedure was to use the speed of light and the Rydberg constant of Hydrogen to derive the natural units of 4.558816×10-8 m for space and 1.520655×10-16 sec, for time.
However, Borg used a different procedure, to derive the much smaller natural units of 4.051319933x10-35 m, for space and 1.351374868x10-43, for time.
This difference in the magnitude of natural units has obvious consequences in the development of theoretical values, especially given that the LST's mass unit of kilograms is an arbitrary one in the SI system, treated by Borg, but Larson also realized that this complication had to be taken into account, as he explains:
Yet, this is not all. The dimensions of the "energy group" of units are subject to another aspect of confusion, which Larson attributes to the fact that, in the RST, unlike in the LST, gravity is not a force between masses, but simply the independent inward scalar motion of matter.
As Larson explains it, the gravitational force equation is an observed equality, not a defined equality. Therefore, it must be analyzed in such a way as will reflect its true space and time dimensions, which he argues are
(s3/t3 × t3/s3) × t/s2 = t/s2
Of course, Borg cannot consider this argument, as it is incorporates an incomprehensible concept in the LST, but he uses what he describes as "Planck constants," to calculate the natural units of space and time, and then, using those, he arrives at a mass conversion constant, 1.469944166x1018, which, when multiplied by his natural mass unit, with dimensions t3/s3, yields the correct value of the SI mass unit called the kilogram.
With this dimensionless conversion factor, Borg then goes on to calculate two other conversion factors and then, with these three, he calculates the values of many observed physical constants and asserts that any physical constant whatsoever can be calculated in this manner.
Hopefully, I haven't confused the reader to this point, but if so, please refer to chapter 13 of Nothing But Motion, and Borg's paper linked above, to study more of the details.
The bottom line here is that taking Borg's work on dimensions of natural and conventional units together with Larson's work on reciprocity, we may have a better chance to translate between the LST-based results of Mills and Borg and the RST-based results of the LRC's RSt.
I see it as a preliminary and necessary step to constructing a new language of scalar mathematics, whereby we can simplify the complicated and baroque and obtuse vector mathematics, used by the LST community, to the same degree, more or less, that the S/T and T/S system of physical units simplify the SI system.
As I said, it's a terrific challenge that were up against.
Recall, that Borg's clarification of the SI system of units, shows that mass, in units of kilograms, a central unit of the SI system of measurement units, is, after all, "a fictitious unit."

His analysis of the SI mass unit and others is fascinating (see here), if unacknowledged by the greater LST community. Of course, these things take time, lots of it, so it may be centuries before he is given the credit he is due in the LST community.
Yet, there is no reason why the RST community should take so long. I didn't know Larson personally, unfortunately, but I'm pretty sure he would have embraced Borg's work wholeheartedly, because the work of the two men fits together so well. Though Borg's work doesn't go so far as to recognize scalar motion and the fundamental implications of the reciprocal nature of space and time, he does recognize their fundamental nature in the physical realm of the LST, which is limited to the material system of the RST.
Borg re-draws the SI diagram shown above to show that, because the space and time units are the only ones that are truly independent, they are the fundamental units in the system, when it's correctly understood:

With this as his starting point, he goes on to show how all physical units and relations between them can be expressed in space and time terms, and gives the procedure for converting the LST dimensions of any formula into what he calls ST dimensions. This is so useful to RST research that it is hard to express the magnitude of it adequately, but it comes down to the value of his insight into the ratio of the natural units of space and time to their conventional units, even though he doesn't recognize the fundamental relation of space and time as scalar motion, as did Larson.
Years ago, I took the liberty to illustrate this simple but vital difference between the work of the two men by modifying Borg's modification of the SI diagram, shown above, to one showing the units from Larson's point of view of fundamental scalar motion:

Students of the RST no doubt delight in the simplicity of the above diagram, but what's more, they realize that it is only the material sector (ms) diagram of physical units. For the cosmic sector (cs), the fundamental units of space and time are inverted, so that the unit of cs scalar motion, T/S, replaces the S/T unit, in the center of the cs version of the diagram (not shown).
How huge is this? It's almost unfathomable. It means that there is a heretofore unknown sector, an inverse sector, to the physical universe, and those of us who are familiar with Larson's works know what marvelous insight into physical phenomena that knowledge provides.
Yet, understanding that revolutionary view of the reciprocal nature of space and time and its tremendous power of clarification of the physical situation does not mean that we can use that power better than the LST community can use their view, which the brightest minds of the world have studied for centuries, regardless of how confusing we now see it is.
For sure, Larson and Borg may have argued over aspects of this situation, but I think both men would have stood their ground in certain areas, and one of those areas where Borg would have prevailed is in the conversion of conventional units to the natural units of space and time.
Larson's procedure was to use the speed of light and the Rydberg constant of Hydrogen to derive the natural units of 4.558816×10-8 m for space and 1.520655×10-16 sec, for time.
However, Borg used a different procedure, to derive the much smaller natural units of 4.051319933x10-35 m, for space and 1.351374868x10-43, for time.
This difference in the magnitude of natural units has obvious consequences in the development of theoretical values, especially given that the LST's mass unit of kilograms is an arbitrary one in the SI system, treated by Borg, but Larson also realized that this complication had to be taken into account, as he explains:
Nevertheless, given the differing values of Borg's natural units of space and time, all the magnitudes of Larson's derived values are going to differ, if Borg is correct, not just those of the energy group.In the case of the quantities of the speed or velocity type, these [values given in a table] are also the values applicable in the conventional systems of measurement. However, mass is regarded as an independent fundamental variable in the conventional systems, and a mass term is introduced into each of the quantities of the energy type. Momentum, for example, is not treated as t2/s2, but as the product of mass and velocity, which, in space-time terms, is t3/s3 × s/t. The use of an arbitrary unit of mass then introduces a numerical factor. Thus, in order to arrive at the values of the natural units in terms of the cgs system of measurement, each of the values given for the energy group in the first column of the tabulation must be divided by this factor: 2.236055×10-8.
Yet, this is not all. The dimensions of the "energy group" of units are subject to another aspect of confusion, which Larson attributes to the fact that, in the RST, unlike in the LST, gravity is not a force between masses, but simply the independent inward scalar motion of matter.
As Larson explains it, the gravitational force equation is an observed equality, not a defined equality. Therefore, it must be analyzed in such a way as will reflect its true space and time dimensions, which he argues are
(s3/t3 × t3/s3) × t/s2 = t/s2
Of course, Borg cannot consider this argument, as it is incorporates an incomprehensible concept in the LST, but he uses what he describes as "Planck constants," to calculate the natural units of space and time, and then, using those, he arrives at a mass conversion constant, 1.469944166x1018, which, when multiplied by his natural mass unit, with dimensions t3/s3, yields the correct value of the SI mass unit called the kilogram.
With this dimensionless conversion factor, Borg then goes on to calculate two other conversion factors and then, with these three, he calculates the values of many observed physical constants and asserts that any physical constant whatsoever can be calculated in this manner.
Hopefully, I haven't confused the reader to this point, but if so, please refer to chapter 13 of Nothing But Motion, and Borg's paper linked above, to study more of the details.
The bottom line here is that taking Borg's work on dimensions of natural and conventional units together with Larson's work on reciprocity, we may have a better chance to translate between the LST-based results of Mills and Borg and the RST-based results of the LRC's RSt.
I see it as a preliminary and necessary step to constructing a new language of scalar mathematics, whereby we can simplify the complicated and baroque and obtuse vector mathematics, used by the LST community, to the same degree, more or less, that the S/T and T/S system of physical units simplify the SI system.
As I said, it's a terrific challenge that were up against.
Re: Meeting a Terrific Challenge
Knowing the confusion introduced by the measurement systems of the LST community, as clarified by Xavier Borg, which results in the mis-comprehension of the dimensions of the energy group of physical constants, as clarified by Larson, helps us tremendously in our efforts to develop an RST-based theory, or RSt.
With the work of these men, we can clearly see that the dimensions of physical units in the material sector (ms) are the dimensions of velocity, space/time units (s/t), while the dimensions of physical units in the cosmic sector (cs) are time/space units (t/s).
Though the LST community totally rejects any theoretical entity with dimensions of inverse velocity, which they interpret as magnitudes of vector motion with greater-than-light speed, their concept of energy, with dimensions t/s, permits them to accommodate the misunderstanding.
In the RST, however, ms energy, with dimensions t/s, is just cs velocity, or motion in time, while ms velocity, with dimensions s/t, is just cs energy, or motion in space, and while this concept of reciprocity is simple to understand, once it is explained properly, it's not that easy to keep the consequences of this theoretical proposition straight, as we develop the theory and seek to compare the results with observations expressed in terms of the vector motion-based LST.
The major difference between the RST and the LST is the incorporation of the concept of scalar motion in the former that is unrecognized in the latter. Scalar motion, by definition, is a ratio of change in space and time units, but it is a change in the size, or the scale of the space/time ratio, not a change in the position or location of an object, as defined in vector motion.
As Larson developed his RST-based RSt, he avoided expressing his scalar concepts mathematically, as much as possible, making it difficult to know for sure exactly what it was he was saying. This frequently led to a call for a mathematical formalism of his theory, but he contended that it was not necessary, because the mathematics of the LST sufficed, when the existing equations were properly interpreted. In a letter to Frank Meyer, two years before Frank passed away, Larson wrote:
Nevertheless, our investigations show otherwise, because not only is there confusion in the physical units of the LST systems of measurement, as explained by Borg, and confusion with respect to the dimensions of the energy group of physical constants, as explained by Larson, but there is also confusion in the units of the LST mathematics, as explained by this investigator.
As it turns out, in the LRC's RSt, the fundamental scalar motion is not the 1D scalar vibration of Larson's RSt, which rotates as a propeller in a second dimension, forming a 2D disk, which, when flipped as a tossed coin, forms a 3D sphere, which is then utilized as the basic building block of scalar motions to be combined into higher and higher combinations of scalar motion, the relations between which explain physical phenomena.
To the contrary, our RSt begins and ends with 3D, scalar oscillations, combinations of these, and relations between them, and as such the theoretical entities formed have intrinsic 1D, 2D and 3D components, and the relation between these produce 1D, 2D and 3D physical phenomena, such as electric monopole, magnetic dipole and gravitic quadrupole phenomena, that can only be properly understood using a new scalar algebra, which is unrecognized in the mathematics of LST science.
Of course, if there is to be any hope of validating a scalar approach to multi-dimensional mathematics, we not only have to understand the scalar concepts it may be based on, but also how these relate to the concepts of the established vector mathematics used by the LST community.
Though, to be sure, this is an impossible task to complete in any sense of the word, perhaps we can begin it, by looking at the fundamentals, as Larson and Borg have done. In our investigations to date, we have discovered that the group of rational numbers (1/n, ...1/3, 1/2, 1/1, 2/1, 3/1, ...n/1) is isomorphic to the logical combinations of 3D scalar motion oscillations, developed in our RSt, as I have explained them in previous posts of this discussion of LRC Research.
This is a fortuitous discovery, since it permits us to formulate the fundamental combinations of these scalar oscillations mathematically, as
S|T = 1/2+1/1+2/1 = 4|4 ..............................................................(1)
where S is an instance of space oscillation over time, s/t, and T is an instance of time oscillation over space, but with inverted time/space dimensions, to match the dimensions of the S unit.
The total motion of equation (1) is always balanced (i.e. equal), while its outer terms are never balanced terms. However, the middle term may be either balanced or not, depending upon the relative values of the outer terms.
The algebra is straight forward, but both the addition and multiplication operations require us to add/multiply both the denominator and the numerator of the three terms. Thus, adding the denominators of equation (1) together sums to 4 and adding the numerators also sums to 4. Multiplying the equation by x, we write:
x(S|T) = x(1/2+1/1+2/1) = (x1/x2+x1/x1+x2/x1) = x(4|4)..................................................(2)
Of course, this is just the start, as the units of equation (1) may be non-integer values, as well, although not actually non-rational values in the sense understood in the LST community. In the scalar mathematics of the RSt, there are only discrete units, as required by the postulates of the system. However, given that the fundamental oscillations of the system are 3D, there are actually three different units that can be identified, within the oscillating volume.
To understand this, we have to recognize that the scalar oscillation in three dimensions is necessarily spherical, but the equivalent scalar mathematical formulation of that expansion is not. When a scalar expansion of a point is expressed, in a 3D coordinate system, and the change is effective in all three dimensions of that system, the mathematics expands two "directions" for each dimension:
21 = 2,
22 = 2x2 = 4,
23 = 2x2x2 = 8.
Therefore, the 3D mathematical expansion, 2x2x2 = 8 expresses a 3D stack of 8 one-unit cubes, but the algebra doesn't tell us that. Only if we interpret the operation geometrically and posit that the two "directions" are opposite "directions" do we arrive at this understanding of the mathematics. Larson had a lot to say about this, and you can read some of it here.
Consequently, it's plain to see that there is a mismatch between the physical spherical expansion, posited in our RSt oscillations, and the mathematical/geometrical expansion of the rational numbers of equation (1). It really comes down to the most fundamental scientific challenge of mankind: How do we reconcile analog magnitudes of geometry with the discrete magnitudes of numbers? It's simply put as the age-old challenge of "squaring the circle."
If we assign the normal exponents denoting dimensions to the rational numbers of equation (1), the results will not reflect the physical situation correctly. This is true primarily because 10 = 11 = 12 =13 in LST algebra, but not in our physical oscillation.
What is needed is a multi-dimensional scalar unit, where 10 ≠ 11 ≠ 12 ≠ 13, but 1 = 20, 1 = 21, 1 = 22, 1 = 23, respectively. In other words, a unit point, a unit line, a unit square and a unit volume, with two "directions" in each dimension!
This was a real challenge in the beginning, since we needed the mathematical operators, as well as the geometrical operands, in our scalar equations. However, I think that the answer to the question of how to integrate the two is found in the Pythagorean theorem, which will be discussed next.
With the work of these men, we can clearly see that the dimensions of physical units in the material sector (ms) are the dimensions of velocity, space/time units (s/t), while the dimensions of physical units in the cosmic sector (cs) are time/space units (t/s).
Though the LST community totally rejects any theoretical entity with dimensions of inverse velocity, which they interpret as magnitudes of vector motion with greater-than-light speed, their concept of energy, with dimensions t/s, permits them to accommodate the misunderstanding.
In the RST, however, ms energy, with dimensions t/s, is just cs velocity, or motion in time, while ms velocity, with dimensions s/t, is just cs energy, or motion in space, and while this concept of reciprocity is simple to understand, once it is explained properly, it's not that easy to keep the consequences of this theoretical proposition straight, as we develop the theory and seek to compare the results with observations expressed in terms of the vector motion-based LST.
The major difference between the RST and the LST is the incorporation of the concept of scalar motion in the former that is unrecognized in the latter. Scalar motion, by definition, is a ratio of change in space and time units, but it is a change in the size, or the scale of the space/time ratio, not a change in the position or location of an object, as defined in vector motion.
As Larson developed his RST-based RSt, he avoided expressing his scalar concepts mathematically, as much as possible, making it difficult to know for sure exactly what it was he was saying. This frequently led to a call for a mathematical formalism of his theory, but he contended that it was not necessary, because the mathematics of the LST sufficed, when the existing equations were properly interpreted. In a letter to Frank Meyer, two years before Frank passed away, Larson wrote:
As I have tried to emphasize throughout my writings, the conceptual aspects of physical theory, our understanding of what the mathematics of physical events mean, is independent of the mathematical relations. There are usually many possible interpretations of the same mathematics. Consequently, the true meaning cannot be derived from the mathematics. As matters now stand, the accepted physical meaning of each mathematical relation is based on assumptions applicable to that particular case. Conventional physical theory has a general mathematical structure into which each individual conclusion is required to fit, but it has no similar conceptual structure, and it therefore has no way of verifying the conceptual interpretations of the mathematical relations. Our contribution is to provide the conceptual structure that is needed. Since the previous interpretations were based on unconnected assumptions, it was inevitable that some of them would turn out to be wrong, but this does not necessarily mean that the mathematical expressions are incorrect. And where we do find that some modification of the mathematical relations is necessary, we do not need any new kind of mathematics.
Nevertheless, our investigations show otherwise, because not only is there confusion in the physical units of the LST systems of measurement, as explained by Borg, and confusion with respect to the dimensions of the energy group of physical constants, as explained by Larson, but there is also confusion in the units of the LST mathematics, as explained by this investigator.
As it turns out, in the LRC's RSt, the fundamental scalar motion is not the 1D scalar vibration of Larson's RSt, which rotates as a propeller in a second dimension, forming a 2D disk, which, when flipped as a tossed coin, forms a 3D sphere, which is then utilized as the basic building block of scalar motions to be combined into higher and higher combinations of scalar motion, the relations between which explain physical phenomena.
To the contrary, our RSt begins and ends with 3D, scalar oscillations, combinations of these, and relations between them, and as such the theoretical entities formed have intrinsic 1D, 2D and 3D components, and the relation between these produce 1D, 2D and 3D physical phenomena, such as electric monopole, magnetic dipole and gravitic quadrupole phenomena, that can only be properly understood using a new scalar algebra, which is unrecognized in the mathematics of LST science.
Of course, if there is to be any hope of validating a scalar approach to multi-dimensional mathematics, we not only have to understand the scalar concepts it may be based on, but also how these relate to the concepts of the established vector mathematics used by the LST community.
Though, to be sure, this is an impossible task to complete in any sense of the word, perhaps we can begin it, by looking at the fundamentals, as Larson and Borg have done. In our investigations to date, we have discovered that the group of rational numbers (1/n, ...1/3, 1/2, 1/1, 2/1, 3/1, ...n/1) is isomorphic to the logical combinations of 3D scalar motion oscillations, developed in our RSt, as I have explained them in previous posts of this discussion of LRC Research.
This is a fortuitous discovery, since it permits us to formulate the fundamental combinations of these scalar oscillations mathematically, as
S|T = 1/2+1/1+2/1 = 4|4 ..............................................................(1)
where S is an instance of space oscillation over time, s/t, and T is an instance of time oscillation over space, but with inverted time/space dimensions, to match the dimensions of the S unit.
The total motion of equation (1) is always balanced (i.e. equal), while its outer terms are never balanced terms. However, the middle term may be either balanced or not, depending upon the relative values of the outer terms.
The algebra is straight forward, but both the addition and multiplication operations require us to add/multiply both the denominator and the numerator of the three terms. Thus, adding the denominators of equation (1) together sums to 4 and adding the numerators also sums to 4. Multiplying the equation by x, we write:
x(S|T) = x(1/2+1/1+2/1) = (x1/x2+x1/x1+x2/x1) = x(4|4)..................................................(2)
Of course, this is just the start, as the units of equation (1) may be non-integer values, as well, although not actually non-rational values in the sense understood in the LST community. In the scalar mathematics of the RSt, there are only discrete units, as required by the postulates of the system. However, given that the fundamental oscillations of the system are 3D, there are actually three different units that can be identified, within the oscillating volume.
To understand this, we have to recognize that the scalar oscillation in three dimensions is necessarily spherical, but the equivalent scalar mathematical formulation of that expansion is not. When a scalar expansion of a point is expressed, in a 3D coordinate system, and the change is effective in all three dimensions of that system, the mathematics expands two "directions" for each dimension:
21 = 2,
22 = 2x2 = 4,
23 = 2x2x2 = 8.
Therefore, the 3D mathematical expansion, 2x2x2 = 8 expresses a 3D stack of 8 one-unit cubes, but the algebra doesn't tell us that. Only if we interpret the operation geometrically and posit that the two "directions" are opposite "directions" do we arrive at this understanding of the mathematics. Larson had a lot to say about this, and you can read some of it here.
Consequently, it's plain to see that there is a mismatch between the physical spherical expansion, posited in our RSt oscillations, and the mathematical/geometrical expansion of the rational numbers of equation (1). It really comes down to the most fundamental scientific challenge of mankind: How do we reconcile analog magnitudes of geometry with the discrete magnitudes of numbers? It's simply put as the age-old challenge of "squaring the circle."
If we assign the normal exponents denoting dimensions to the rational numbers of equation (1), the results will not reflect the physical situation correctly. This is true primarily because 10 = 11 = 12 =13 in LST algebra, but not in our physical oscillation.
What is needed is a multi-dimensional scalar unit, where 10 ≠ 11 ≠ 12 ≠ 13, but 1 = 20, 1 = 21, 1 = 22, 1 = 23, respectively. In other words, a unit point, a unit line, a unit square and a unit volume, with two "directions" in each dimension!
This was a real challenge in the beginning, since we needed the mathematical operators, as well as the geometrical operands, in our scalar equations. However, I think that the answer to the question of how to integrate the two is found in the Pythagorean theorem, which will be discussed next.
Re: Meeting a Terrific Challenge
The story of Pythagoras and the Pythagorean theorem is fascinating, but it's the connection to the story of Euclidean geometry, and the development of algebra, and on to the saga of Newton's Laws and the struggle to understand irrational numbers, imaginary numbers and vector algebra, and all the characters involved in the struggle, which fascinates the heck out of me.
The properties of the right triangle seem to sum it all up, actually. The fact that the square root of the sum of the squares of the sides of the unit triangle is an irrational number not only destroyed the secret society of the Pythagoreans eventually, but went on from there to cause havoc in any number of ways for the efforts of mankind to understand nature. And it still does, as the transition from analog physics to discrete physics has caused the science of mankind to become stuck in a theoretical morass, which seems impossible to escape.
Now, Randell Mills comes along and finds a way out by going back in time, or so it seems. Nevertheless, even if his GUT explains much more in terms of analog physics, than can be explained in terms of discrete physics, the fact remains that it can't begin to explain it all, if Larson's fundamental postulates hold, because it is unaware of scalar motion.
In the previous post, I showed how our need for a mathematical formalism of scalar motion has led to the equation,
S|T = 1/2+1/1+2/1 = 4|4, ......................................................................(1)
in the LRC's work to develop an RSt mathematically.
The work has been very successful in term of formulating the one-dimensional magnitudes of equation (1), but the two-dimensional and three-dimensional magnitudes, necessary to describe the magnetic and gravitic properties of these theoretical entities is another matter entirely.
As it turns out, we need a 2D and a 3D scalar unit, in addition to the 1D scalar unit we have now. Presumably, these multi-dimensional units would enter into equation (1) in the same manner as the 1D units do; that is, they they would substitute for the 1D units in the equation. For the nD equation, we would have,
S|T = 1n/2n+1n/1n+2n/1n = 4n|4n, ......................................................................(2)
but not where n = nx, denoting the dimension of the unit.
Instead, n for the 1D unit equals √1 and for the 2D unit it equals √2 and for the 3D unit it equals √3.
This may seem to be a bizarre proposition, but there is a very sound reason for it, illustrated by the graphic below:
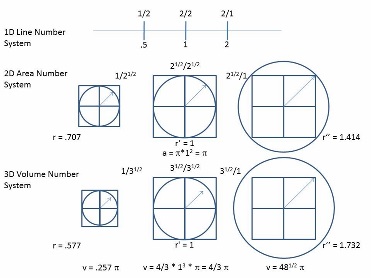
Figure 1. The Three Number Lines of a Three dimensional Scalar Number System
To understand what is illustrated in figure 1, recall that the equation,
23 = 2x2x2 = 8, ..........................................................(3)
can be interpreted geometrically as a stack of 8, one-unit cubes, as shown in the previous post. We call this stack Larson's Cube (LC), because he referred to it in explaining the eight "directions" of 3D magnitudes, but we use it to construct the multi-dimensional unit, n, for equation (2), using the Pythagorean Theorem, in three dimensions,
n = √(a2+b2+c2) ............................................................(4)
For the 1D unit, a is equal to 1, while b and c are equal to zero; For the 2D unit, a and b are equal to 1 and c is equal to zero, and for the 3D unit, a = b = c = 1.
Thus, the 1D unit is equal to the √1, the 2D unit is equal to the √2, and the 3D unit is equal to the √3. Each unit forms its own number line of magnitudes and inverse magnitudes, as shown in figure 1 (Note: The accompanying illustration for the length of the radius of the 3D figure is incorrect).
The rationale for pursuing this course is found in the geometrical relationship of LC to the ball that just fits within it and the ball that just contains it, referred to as the inner and outer ball respectively. While the radius of the inner ball is the √1, the radius of the outer ball is the √3, by the Pythagorean Theorem, but both are determined by the magnitude of LC.
Therefore, given equation (3), as a formulation of a 3D expansion in eight "directions," the magnitude of the radii of the two balls is also determined, and while the radius of the inner ball is equal to √1, the radius of a 2D slice of the balls and the cube, at the equator, is equal to the diagonal of LC, or the √2. Thus, all three unit magnitudes, √1, √2, and the √3, are intrinsic properties of LC.
Consequently, the three number lines are isomorphic to the rational number group, meaning that the variable, n, of equation (4) can be the value of any one of the units:
1) S|T = 1(√1)/2(√1)+1(√1)/1(√1)+2(√1)/1(√1) = 4(√1)|4(√1),
2) S2|T2 = 1(√2)/2(√2)+1(√2)/1(√2)+2(√2)/1(√2) = 4(√2)|4(√2),
3) S3|T3 = 1(√3)/2(√3)+1(√3)/1(√3)+2(√3)/1(√3) = 4(√3)|4(√3).
Now, the three number lines of figure 1 may seem a bit strange at first, since the unit value is shown both as 1 (1/1) and 2/2, but the reason for this is that, in the case of oscillation, the number 1/1 doesn't exist, since it takes 2 units to complete one cycle of oscillation.
Yet, for some reason, that point was neglected for the 2D and 3D lines. For our purposes, the chart of figure 1 should be revised to show the correct number line as,
...1n/2n, 2n/2n, 2n/1n...
In the LST, 2D magnitudes of velocity are replaced with 2D magnitudes of energy, momentum (t2/s2), by using the kilogram unit of mass times velocity,
p = m x v (or t2/s2 = t3/s3 x s/t)
and this is used in the model of the atom as a quantity of angular momentum, h, of the orbiting electron,
h = r x p (or t2/s = s x t2/s2).
In the scalar motion of the atom, there is no orbiting electron or orbiting current, as in the new atomic model of Mills, but only oscillating scalar motions. Yet, we have seen a marvelous revelation of scalar motion equivalents of electric charge in these scalar combos, explaining the play of positive and negative "charges" in the proton, neutron and electron relations and in the positive and negative beta decay processes.
It's hard to believe that these and other successes could be simple coincidences, but you never know. The next step is to see if we can find similar "coincidences" in the realm of the 2D (magnetic) and 3D (mass) properties of these scalar motion combos.
Now that we have a multi-dimensional scalar algebra, I'm optimistic.
The properties of the right triangle seem to sum it all up, actually. The fact that the square root of the sum of the squares of the sides of the unit triangle is an irrational number not only destroyed the secret society of the Pythagoreans eventually, but went on from there to cause havoc in any number of ways for the efforts of mankind to understand nature. And it still does, as the transition from analog physics to discrete physics has caused the science of mankind to become stuck in a theoretical morass, which seems impossible to escape.
Now, Randell Mills comes along and finds a way out by going back in time, or so it seems. Nevertheless, even if his GUT explains much more in terms of analog physics, than can be explained in terms of discrete physics, the fact remains that it can't begin to explain it all, if Larson's fundamental postulates hold, because it is unaware of scalar motion.
In the previous post, I showed how our need for a mathematical formalism of scalar motion has led to the equation,
S|T = 1/2+1/1+2/1 = 4|4, ......................................................................(1)
in the LRC's work to develop an RSt mathematically.
The work has been very successful in term of formulating the one-dimensional magnitudes of equation (1), but the two-dimensional and three-dimensional magnitudes, necessary to describe the magnetic and gravitic properties of these theoretical entities is another matter entirely.
As it turns out, we need a 2D and a 3D scalar unit, in addition to the 1D scalar unit we have now. Presumably, these multi-dimensional units would enter into equation (1) in the same manner as the 1D units do; that is, they they would substitute for the 1D units in the equation. For the nD equation, we would have,
S|T = 1n/2n+1n/1n+2n/1n = 4n|4n, ......................................................................(2)
but not where n = nx, denoting the dimension of the unit.
Instead, n for the 1D unit equals √1 and for the 2D unit it equals √2 and for the 3D unit it equals √3.
This may seem to be a bizarre proposition, but there is a very sound reason for it, illustrated by the graphic below:

Figure 1. The Three Number Lines of a Three dimensional Scalar Number System
To understand what is illustrated in figure 1, recall that the equation,
23 = 2x2x2 = 8, ..........................................................(3)
can be interpreted geometrically as a stack of 8, one-unit cubes, as shown in the previous post. We call this stack Larson's Cube (LC), because he referred to it in explaining the eight "directions" of 3D magnitudes, but we use it to construct the multi-dimensional unit, n, for equation (2), using the Pythagorean Theorem, in three dimensions,
n = √(a2+b2+c2) ............................................................(4)
For the 1D unit, a is equal to 1, while b and c are equal to zero; For the 2D unit, a and b are equal to 1 and c is equal to zero, and for the 3D unit, a = b = c = 1.
Thus, the 1D unit is equal to the √1, the 2D unit is equal to the √2, and the 3D unit is equal to the √3. Each unit forms its own number line of magnitudes and inverse magnitudes, as shown in figure 1 (Note: The accompanying illustration for the length of the radius of the 3D figure is incorrect).
The rationale for pursuing this course is found in the geometrical relationship of LC to the ball that just fits within it and the ball that just contains it, referred to as the inner and outer ball respectively. While the radius of the inner ball is the √1, the radius of the outer ball is the √3, by the Pythagorean Theorem, but both are determined by the magnitude of LC.
Therefore, given equation (3), as a formulation of a 3D expansion in eight "directions," the magnitude of the radii of the two balls is also determined, and while the radius of the inner ball is equal to √1, the radius of a 2D slice of the balls and the cube, at the equator, is equal to the diagonal of LC, or the √2. Thus, all three unit magnitudes, √1, √2, and the √3, are intrinsic properties of LC.
Consequently, the three number lines are isomorphic to the rational number group, meaning that the variable, n, of equation (4) can be the value of any one of the units:
1) S|T = 1(√1)/2(√1)+1(√1)/1(√1)+2(√1)/1(√1) = 4(√1)|4(√1),
2) S2|T2 = 1(√2)/2(√2)+1(√2)/1(√2)+2(√2)/1(√2) = 4(√2)|4(√2),
3) S3|T3 = 1(√3)/2(√3)+1(√3)/1(√3)+2(√3)/1(√3) = 4(√3)|4(√3).
Now, the three number lines of figure 1 may seem a bit strange at first, since the unit value is shown both as 1 (1/1) and 2/2, but the reason for this is that, in the case of oscillation, the number 1/1 doesn't exist, since it takes 2 units to complete one cycle of oscillation.
Yet, for some reason, that point was neglected for the 2D and 3D lines. For our purposes, the chart of figure 1 should be revised to show the correct number line as,
...1n/2n, 2n/2n, 2n/1n...
In the LST, 2D magnitudes of velocity are replaced with 2D magnitudes of energy, momentum (t2/s2), by using the kilogram unit of mass times velocity,
p = m x v (or t2/s2 = t3/s3 x s/t)
and this is used in the model of the atom as a quantity of angular momentum, h, of the orbiting electron,
h = r x p (or t2/s = s x t2/s2).
In the scalar motion of the atom, there is no orbiting electron or orbiting current, as in the new atomic model of Mills, but only oscillating scalar motions. Yet, we have seen a marvelous revelation of scalar motion equivalents of electric charge in these scalar combos, explaining the play of positive and negative "charges" in the proton, neutron and electron relations and in the positive and negative beta decay processes.
It's hard to believe that these and other successes could be simple coincidences, but you never know. The next step is to see if we can find similar "coincidences" in the realm of the 2D (magnetic) and 3D (mass) properties of these scalar motion combos.
Now that we have a multi-dimensional scalar algebra, I'm optimistic.
Re: Meeting a Terrific Challenge
The need to translate between the LST's vectorial motion concepts, expressed in terms of SI units, and scalar motion concepts, expressed in terms of natural units of space and time is obvious. Of course, Larson was the first to attempt it, in the development of his RSt, as can be found in Chapter 13 of NBM.
But since his RSt is based on a rotation of a 1D oscillation, and the LRC's RSt is based on 3D oscillations, his procedure for determining the magnitude of the natural units of space and time may not be applicable. Besides that, coming from the LST community perspective, Xavior Borg's calculations show much smaller magnitudes for the natural units of space and time.
Whose values are correct? Can they be reconciled somehow? That is the question that must be answered in light of the terrific challenge we face to develop a scalar algebra suitable for calculating theoretical values, which correspond to observed values, as close as do those of Randell Mills, which are very, very close, in contrast to QM calculations.
Mills has rejected the quantum mechanics approach for the most part, which he considers mathematical only, or "non-physical," and has gone back in time to the model of the Bohr atom, where his solution to the radiation of a point charge surrounding the nucleus is a lot like the standing wave approach of Bohr, but without the concept of duality, the wave/particle nature of quantum mechanics.
In both models, the classical physics concept of "balance of forces" is key. The idea is to balance the potential and kinetic energy, given the total energy of the system, just as it is in the classical case of the oscillating pendulum. So, in the Bohr model, the point charge of the electron orbits the nucleus and, like a planet orbiting a star, the radius of the orbit is determined by the laws of Newton, but the electrostatic force replaces the gravitic force in the force balance equation:
 ....................................................(1)
....................................................(1)
In the Mills model, the point charge of the electron mass is replaced by an eggshell-like sphere of charge currents, as if a circle of current has been rotated, sweeping out a sphere around the nucleus, thus avoiding the need to invoke the dual particle/wave nature of the electron to get around its radiation problem. The basic idea to overcome is that an orbiting mass like the electron has to radiate energy, because of the acceleration forces inherent in the continuous change of direction of the orbit, but Mills read that a continuous loop of current does not radiate.
Consequently, he decided to investigate the theoretical results of substituting this non-radiating loop of current, spread over a spherical surface, surrounding the proton, for the standing wave of Bohr's orbiting electron point charge.
There are other important differences between the Bohr model and Mills' modification of it, but the most relevant point for our purposes is that both models depend on this balance of forces: The electrostatic force side of equation (1) for the Bohr model calculates the attractive electrostatic force required to balance out the centrifugal force of the orbiting electron mass, to keep the electron in its orbit, provided it doesn't radiate away its energy, due to the forces of acceleration.
By a tortured process of algebraic substitution, it can be shown that the angular momentum, and thus the energy, of a charged, non radiating mass, orbiting a stationary charge, must be quantized in units that are equivalent to units of h bar.
The major, or principle, difference, then, between Bohr's model and Mills' model is this "quantization condition," or rationalization for how the energy is quantized in the atom. For Bohr, it was the fixed number of wave-lengths that could fit the allowed orbital radii, but for Mills, it is the allowed magnitudes of angular momentum, which determine the size of the orbitsphere, that is the "quantization condition" of his model.
Of course, in an RST-based theory, like ours, there is no moving mass, no angular momentum, which can be quantized by the vector motion of orbiting charges or circulating currents. There is only a combination of 3D oscillations in the LRC's RSt. We START with quantized motion, but it is scalar motion, not vector motion. So, how does one go about calculating the observables in this scalar motion model of the atom? We think that the answer, at least in part, is given by our scalar motion equation,
Sx|Tx = 1n/2n+1n/1n+2n/1n = 4n|4n, ...............................................................(2)
which is a balance of opposing scalar motions, not a balance of "forces," as defined by Newton. As I explained in the previous post, the exponent, x, in equation (2) is determined by three values of n: When n is = √1, the exponent, x, indicating the dimension of the equation, is equal to 1; When n is = √2, the exponent, x, is equal to 2; When n is = √3, the exponent is equal to 3.
As shown already in previous posts of this discussion, the equation works out great for one-dimensional electrical "charges," when x = 1, but it remains to be shown how it works out for higher dimensional properties.
Our model of the atom is static, as far as vector motion is concerned. It has no moving parts other than the 3D oscillations themselves, which are scalar oscillations, or changes in size, not changes in location. over time. The positive "charge" of the proton is the net combination of the scalar motions of its 23 Ss and Ts, while the negative "charge" of the electron is the net combination of the scalar motions of its 9 Ss and Ts.
In our scalar model, the positive "charge" of the proton is due to its excess of 3 Ts, while the negative "charge" of the electron is due its excess of 3 Ss, when these sums are 1D (i.e. x =1). However, these net magnitudes are not 1D when x = 2, or x = 3, of course, they are 2D and 3D sums, respectively.
On this basis, we can see that adding scalar motion in discrete units, as we do, can be calculated in any of the three dimensions, whether its the 2D motion identifiable with momentum, or the 3D motion, identifiable with mass. In any event, it's the translation between the magnitudes of the physical observables, as measured in the LST system, and the calculations of the RSt theoretical magnitudes, using its natural units, that's going to confirm the results.
We've succeeded to some extent with the simple 1D calculations, showing that the positive (time motion) side of equation (2) for the proton and the negative (space motion) side of the electron, balances, without any need to resort to the general force equations of Newton, or the electrostatic force equations of Coulomb.
As already pointed out, ignorant of the RST concept of energy as scalar time-motion, or inverse scalar space-motion, native to the cosmic sector (cs) of the universe, the LST community has defined units of momentum, p, with time/space dimensions, t2/s2, using the dimensions of mass times velocity, or p = mv, and angular momentum, pθ, as mass times velocity times radius, pθ = mvr.
However, in our new RST-based theory, t2/s2 is the two-dimensional version of cs velocity, t/s. which is calculated from equation (2), by setting n = to the √2, but it is expressed in that equation as superluminal s/t velocity, where the numerator is greater than the denominator.
Recall that plugging the proton, electron and photon into equation (2), when n = √1, we get:
P = (46|46)1 num;
e = (18|18)1 num;
γ = (12|12)1 num;
and the total motion for the H atom is just the sum of the first two entities, the proton and the electron:
H1 = (64|64)1 num,
where the subscript 1 denotes the ground state of the atom.
Adding a photon of unspecified frequency to the H atom, we get
H2 = (76|76)1 num;
However, the photon is a balanced space|time motion and does not affect the opposed balance of the positive and negative "charges" of the electron (-3) or the proton (+3), even though it does change the total natural units of motion (num), from 64 to 76.
Moreover, the total motion summed in these equations, where n = √1, is 1D motion, while the unit speed of the propagation of the photon makes it effective in two dimensions (think of the profile of a volume impacting a surface.) Considering this fact, we set the n value of equation (2) for the photon to n = √2, which gives us the two-dimensional, expanded equation for the photon,
(S|T)2 = 3((√2/2(√2))+(√2/√2)+(2(√2)/√2) = 12√2|12√2,
therefore,
γ2 = (√288|√288) num2.
Of course, our natural units are not mathematical square units, but area units of a circle (πr2). These are inverted units of t2/s2 scalar motion, or over unity s2/t2 units, but since t/s velocity is actually motion in time, it only appears to be over-unity, when expressed that way. In reality, it's not any more over-unity than our space oscillation, when viewed from the correct point of view in the cs.
So, we now have a photon with the 2D scalar motion property that is the equivalent of vector momentum, at least qualitatively speaking, even though it doesn't have any ms momentum at all. It's simply a combination of motion in space and motion in time, with 1, 2 and 3D properties. This is a good start, but there is still a long way to go, before we can make the transition, from vector motion concepts of the LST, to the scalar motion concepts of our RSt.
One of the next things we need to do is modify equation (2), yet again.
But since his RSt is based on a rotation of a 1D oscillation, and the LRC's RSt is based on 3D oscillations, his procedure for determining the magnitude of the natural units of space and time may not be applicable. Besides that, coming from the LST community perspective, Xavior Borg's calculations show much smaller magnitudes for the natural units of space and time.
Whose values are correct? Can they be reconciled somehow? That is the question that must be answered in light of the terrific challenge we face to develop a scalar algebra suitable for calculating theoretical values, which correspond to observed values, as close as do those of Randell Mills, which are very, very close, in contrast to QM calculations.
Mills has rejected the quantum mechanics approach for the most part, which he considers mathematical only, or "non-physical," and has gone back in time to the model of the Bohr atom, where his solution to the radiation of a point charge surrounding the nucleus is a lot like the standing wave approach of Bohr, but without the concept of duality, the wave/particle nature of quantum mechanics.
In both models, the classical physics concept of "balance of forces" is key. The idea is to balance the potential and kinetic energy, given the total energy of the system, just as it is in the classical case of the oscillating pendulum. So, in the Bohr model, the point charge of the electron orbits the nucleus and, like a planet orbiting a star, the radius of the orbit is determined by the laws of Newton, but the electrostatic force replaces the gravitic force in the force balance equation:
In the Mills model, the point charge of the electron mass is replaced by an eggshell-like sphere of charge currents, as if a circle of current has been rotated, sweeping out a sphere around the nucleus, thus avoiding the need to invoke the dual particle/wave nature of the electron to get around its radiation problem. The basic idea to overcome is that an orbiting mass like the electron has to radiate energy, because of the acceleration forces inherent in the continuous change of direction of the orbit, but Mills read that a continuous loop of current does not radiate.
Consequently, he decided to investigate the theoretical results of substituting this non-radiating loop of current, spread over a spherical surface, surrounding the proton, for the standing wave of Bohr's orbiting electron point charge.
There are other important differences between the Bohr model and Mills' modification of it, but the most relevant point for our purposes is that both models depend on this balance of forces: The electrostatic force side of equation (1) for the Bohr model calculates the attractive electrostatic force required to balance out the centrifugal force of the orbiting electron mass, to keep the electron in its orbit, provided it doesn't radiate away its energy, due to the forces of acceleration.
By a tortured process of algebraic substitution, it can be shown that the angular momentum, and thus the energy, of a charged, non radiating mass, orbiting a stationary charge, must be quantized in units that are equivalent to units of h bar.
The major, or principle, difference, then, between Bohr's model and Mills' model is this "quantization condition," or rationalization for how the energy is quantized in the atom. For Bohr, it was the fixed number of wave-lengths that could fit the allowed orbital radii, but for Mills, it is the allowed magnitudes of angular momentum, which determine the size of the orbitsphere, that is the "quantization condition" of his model.
Of course, in an RST-based theory, like ours, there is no moving mass, no angular momentum, which can be quantized by the vector motion of orbiting charges or circulating currents. There is only a combination of 3D oscillations in the LRC's RSt. We START with quantized motion, but it is scalar motion, not vector motion. So, how does one go about calculating the observables in this scalar motion model of the atom? We think that the answer, at least in part, is given by our scalar motion equation,
Sx|Tx = 1n/2n+1n/1n+2n/1n = 4n|4n, ...............................................................(2)
which is a balance of opposing scalar motions, not a balance of "forces," as defined by Newton. As I explained in the previous post, the exponent, x, in equation (2) is determined by three values of n: When n is = √1, the exponent, x, indicating the dimension of the equation, is equal to 1; When n is = √2, the exponent, x, is equal to 2; When n is = √3, the exponent is equal to 3.
As shown already in previous posts of this discussion, the equation works out great for one-dimensional electrical "charges," when x = 1, but it remains to be shown how it works out for higher dimensional properties.
Our model of the atom is static, as far as vector motion is concerned. It has no moving parts other than the 3D oscillations themselves, which are scalar oscillations, or changes in size, not changes in location. over time. The positive "charge" of the proton is the net combination of the scalar motions of its 23 Ss and Ts, while the negative "charge" of the electron is the net combination of the scalar motions of its 9 Ss and Ts.
In our scalar model, the positive "charge" of the proton is due to its excess of 3 Ts, while the negative "charge" of the electron is due its excess of 3 Ss, when these sums are 1D (i.e. x =1). However, these net magnitudes are not 1D when x = 2, or x = 3, of course, they are 2D and 3D sums, respectively.
On this basis, we can see that adding scalar motion in discrete units, as we do, can be calculated in any of the three dimensions, whether its the 2D motion identifiable with momentum, or the 3D motion, identifiable with mass. In any event, it's the translation between the magnitudes of the physical observables, as measured in the LST system, and the calculations of the RSt theoretical magnitudes, using its natural units, that's going to confirm the results.
We've succeeded to some extent with the simple 1D calculations, showing that the positive (time motion) side of equation (2) for the proton and the negative (space motion) side of the electron, balances, without any need to resort to the general force equations of Newton, or the electrostatic force equations of Coulomb.
As already pointed out, ignorant of the RST concept of energy as scalar time-motion, or inverse scalar space-motion, native to the cosmic sector (cs) of the universe, the LST community has defined units of momentum, p, with time/space dimensions, t2/s2, using the dimensions of mass times velocity, or p = mv, and angular momentum, pθ, as mass times velocity times radius, pθ = mvr.
However, in our new RST-based theory, t2/s2 is the two-dimensional version of cs velocity, t/s. which is calculated from equation (2), by setting n = to the √2, but it is expressed in that equation as superluminal s/t velocity, where the numerator is greater than the denominator.
Recall that plugging the proton, electron and photon into equation (2), when n = √1, we get:
P = (46|46)1 num;
e = (18|18)1 num;
γ = (12|12)1 num;
and the total motion for the H atom is just the sum of the first two entities, the proton and the electron:
H1 = (64|64)1 num,
where the subscript 1 denotes the ground state of the atom.
Adding a photon of unspecified frequency to the H atom, we get
H2 = (76|76)1 num;
However, the photon is a balanced space|time motion and does not affect the opposed balance of the positive and negative "charges" of the electron (-3) or the proton (+3), even though it does change the total natural units of motion (num), from 64 to 76.
Moreover, the total motion summed in these equations, where n = √1, is 1D motion, while the unit speed of the propagation of the photon makes it effective in two dimensions (think of the profile of a volume impacting a surface.) Considering this fact, we set the n value of equation (2) for the photon to n = √2, which gives us the two-dimensional, expanded equation for the photon,
(S|T)2 = 3((√2/2(√2))+(√2/√2)+(2(√2)/√2) = 12√2|12√2,
therefore,
γ2 = (√288|√288) num2.
Of course, our natural units are not mathematical square units, but area units of a circle (πr2). These are inverted units of t2/s2 scalar motion, or over unity s2/t2 units, but since t/s velocity is actually motion in time, it only appears to be over-unity, when expressed that way. In reality, it's not any more over-unity than our space oscillation, when viewed from the correct point of view in the cs.
So, we now have a photon with the 2D scalar motion property that is the equivalent of vector momentum, at least qualitatively speaking, even though it doesn't have any ms momentum at all. It's simply a combination of motion in space and motion in time, with 1, 2 and 3D properties. This is a good start, but there is still a long way to go, before we can make the transition, from vector motion concepts of the LST, to the scalar motion concepts of our RSt.
One of the next things we need to do is modify equation (2), yet again.
Re: Meeting a Terrific Challenge
One of the most important aspects of Larson new Reciprocal System of Physical Theory is that 3D time has no direction in space and 3D space has no direction in time (see here.)
This is vital to our attempt to formulate scalar equations for use in developing the LRC's RSt. The first equation we formulated as,
S|T = 1/2+1/1+2/1 = 4|4, .................................................................................(1)
helped us tremendously to explore the combinations of discrete scalar motions, but as we seek to advance our theory by investigating higher-dimensional properties, we need to do more than sum the units of scalar motions. We need to formulate the actual scalar motion; that is, we need to formulate the scalar change of space over the scalar change of time, in quantitative terms.
However, this is not that easy to do. Our 3D oscillation is a contracting/expanding volume, with 1D, 2D and 3D components, as explained in previous posts, and, though we have found that we can use the square roots of 1, 2 and 3 to define 1, 2 and 3 dimensional scalar units, the fact that time has no direction in the realm of space motion, that is, it is a scalar magnitude in the material sector (ms), and space has no direction in the realm of time motion, for the same reason, complicates the task to formulate the scalar motions involved, using equation (1).
It's similar to the trouble mathematicians face when they consider what David Hestenes calls the "geometric product" of his Geometric Algebra (GA) (see here for an introduction.)
They are not trained to treat scalars and vectors the way they are treated in GA, but GA has proven very useful to simplify vector algebra and integrate algebra into geometry. Years ago, I envisioned using it in the development of the LRC's RSt, but could not do it, for reasons that will eventually become clear in this discussion.
I used a GA modeling program for a while, which produced great animations, such as the one below, illustrating the geometric product:

The trouble is, it's a vector based way to generate scalar magnitudes. We need a model of a 3D oscillation, based on scalar motion, and a multi-dimensional scalar algebra to manipulate it. We now have the start of just such an algebra, but we need to take it to the next step, and I think the task of translating vector motion concepts inherent in the LST model of the atom, especially the Bohr model, as modified by Mills, into the scalar motion concepts of our RSt model, is a good approach to take, because it really brings the fundamental issues to light.
For instance, if we take the vector motion equation for linear motion, we can illustrate it as the time it takes to move a given distance in a given time, say two units of length, s, in one unit of time, t:
s = ------------------|------------------
t = ---------------------------------------------
v = 2s/t;
Likewise we can illustrate the same for rotational motion, substituting a rotational measure of "space" over time, like substituting 2π radians for the two units of length over one unit of time:
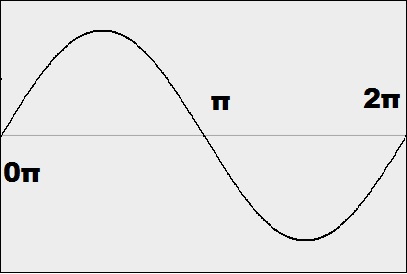
On the same basis, we can illustrate unit scalar motion, substituting a scalar measure of space over time, like substituting two unit areas (πr2) of an expanding/contracting circle over time:
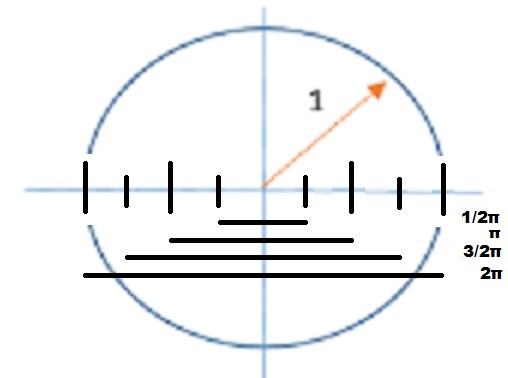
But notice, in the latter case, there is a one-to-one correspondence between the formulation of the rotational motion, measured in units of π radians, and the radial oscillation of the circle, measured in 2D area units:
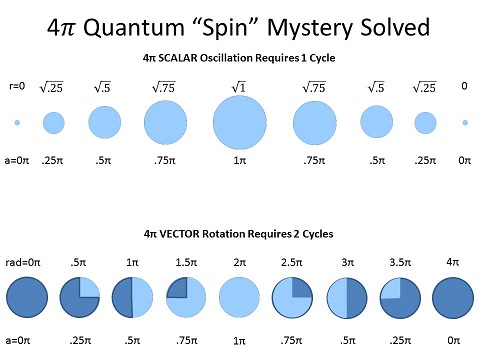
This is because the radial oscillation of the circle is a scalar motion, so it's the diameter of the circle that oscillates, and it expands/contracts in both "directions" of its two dimensions.
As shown in the illustration above, at r = √.25, the area of the expanded circle is actually .25π, which is equivalent to a quarter rotation of the radius of the unit circle, measured as .5π radians; At r = √.5, the area of the expanded circle is .5π, which is equivalent to a rotation of π radians; At r = √.75, it is .75π, which is equivalent to 1.5π radians of rotation, and at r = √1, the area of the circle is equal to π, the equivalent to 2π radians of rotation.
What's even more remarkable than this correspondence with rotational measure is that, at an equivalent of 2π rotation, the expansion is only half-way through its cycle! To contract back to zero where it started, will require another quantity of scalar motion equivalent to 2π rotation, explaining for the first time ever how quantum "spin" equates to 4π rotation per cycle, in the LST!
This is another encouraging sign that we are on the right track, but how do we formulate these observations into an equation of motion? I think the answer lies in recognizing that the oscillation cycle of the Ss and the Ts of equation (1) can be written as,
S = (exp)∪(ctr)/t = 4π/t and,
T = (exp)∪(ctr)/s = 4π/s,
where "exp" and "ctr" are expansion and contraction, respectively. The union of the two halves of the 4π scalar cycle is similar to the union of the two halves of the 2π rotation cycle. The expansion from r = 0 to r = √1, and the contraction from r = √1 back to r = 0, is analogous to a rotation of a unit radius, from 0 to 180 degrees, and from 180 degrees back to 0 degrees, in one unit of cycle time, only it requires an equivalent of two 2π rotations to complete one scalar cycle.
Hence, we combine the numerator of the LH term of equation (1) with the numerator of the middle term, and the denominator of the RH term with the denominator of the middle term. Since, the area of the expanding/contracting circle, given by πr2, at time t, is equal to the area swept out by the rotation of the unit radius, measured in radians, there should be a one-to-one correspondence in the quantitative measures of the two motions, though one be scalar and the other vectorial.
In the scalar case, we have a changing area of space over time, with dimensions, s2/t, as a fraction of unit area, analogous to the vectorial case, where we have a changing angle, measured as a fraction of 2π radians, with dimensions t2/s.
The one is the inverse of the other, just as the LST dimensions of mass are the inverse of the dimension of space motion in the ms. In the vectorial case of the LST science, the dimensions are radius (space) times momentum and the quantity is called angular momentum, the basis of Mills atomic model. In the scalar case, however, the dimensions are simply change of area magnitude over time, where no change of position and no mass are involved.
Thus, the angular momentum of LST theory is just the inverse of the 2D velocity of our RSt theory! Therefore, the LST equation for energy, E = hν, or
t/s = t2/s x 1/t (cycles per unit time),
translates to,
s/t = s2/t x 1/s (cycles per unit space),
in our RSt.
Nevertheless, we cannot afford to change the fundamental measure of the LST at this point, just the fundamental understanding. In reality, t/s is scalar motion in time, but it should be understood as a measure of scalar motion in space.
This is vital to our attempt to formulate scalar equations for use in developing the LRC's RSt. The first equation we formulated as,
S|T = 1/2+1/1+2/1 = 4|4, .................................................................................(1)
helped us tremendously to explore the combinations of discrete scalar motions, but as we seek to advance our theory by investigating higher-dimensional properties, we need to do more than sum the units of scalar motions. We need to formulate the actual scalar motion; that is, we need to formulate the scalar change of space over the scalar change of time, in quantitative terms.
However, this is not that easy to do. Our 3D oscillation is a contracting/expanding volume, with 1D, 2D and 3D components, as explained in previous posts, and, though we have found that we can use the square roots of 1, 2 and 3 to define 1, 2 and 3 dimensional scalar units, the fact that time has no direction in the realm of space motion, that is, it is a scalar magnitude in the material sector (ms), and space has no direction in the realm of time motion, for the same reason, complicates the task to formulate the scalar motions involved, using equation (1).
It's similar to the trouble mathematicians face when they consider what David Hestenes calls the "geometric product" of his Geometric Algebra (GA) (see here for an introduction.)
They are not trained to treat scalars and vectors the way they are treated in GA, but GA has proven very useful to simplify vector algebra and integrate algebra into geometry. Years ago, I envisioned using it in the development of the LRC's RSt, but could not do it, for reasons that will eventually become clear in this discussion.
I used a GA modeling program for a while, which produced great animations, such as the one below, illustrating the geometric product:

The trouble is, it's a vector based way to generate scalar magnitudes. We need a model of a 3D oscillation, based on scalar motion, and a multi-dimensional scalar algebra to manipulate it. We now have the start of just such an algebra, but we need to take it to the next step, and I think the task of translating vector motion concepts inherent in the LST model of the atom, especially the Bohr model, as modified by Mills, into the scalar motion concepts of our RSt model, is a good approach to take, because it really brings the fundamental issues to light.
For instance, if we take the vector motion equation for linear motion, we can illustrate it as the time it takes to move a given distance in a given time, say two units of length, s, in one unit of time, t:
s = ------------------|------------------
t = ---------------------------------------------
v = 2s/t;
Likewise we can illustrate the same for rotational motion, substituting a rotational measure of "space" over time, like substituting 2π radians for the two units of length over one unit of time:

On the same basis, we can illustrate unit scalar motion, substituting a scalar measure of space over time, like substituting two unit areas (πr2) of an expanding/contracting circle over time:

But notice, in the latter case, there is a one-to-one correspondence between the formulation of the rotational motion, measured in units of π radians, and the radial oscillation of the circle, measured in 2D area units:

This is because the radial oscillation of the circle is a scalar motion, so it's the diameter of the circle that oscillates, and it expands/contracts in both "directions" of its two dimensions.
As shown in the illustration above, at r = √.25, the area of the expanded circle is actually .25π, which is equivalent to a quarter rotation of the radius of the unit circle, measured as .5π radians; At r = √.5, the area of the expanded circle is .5π, which is equivalent to a rotation of π radians; At r = √.75, it is .75π, which is equivalent to 1.5π radians of rotation, and at r = √1, the area of the circle is equal to π, the equivalent to 2π radians of rotation.
What's even more remarkable than this correspondence with rotational measure is that, at an equivalent of 2π rotation, the expansion is only half-way through its cycle! To contract back to zero where it started, will require another quantity of scalar motion equivalent to 2π rotation, explaining for the first time ever how quantum "spin" equates to 4π rotation per cycle, in the LST!
This is another encouraging sign that we are on the right track, but how do we formulate these observations into an equation of motion? I think the answer lies in recognizing that the oscillation cycle of the Ss and the Ts of equation (1) can be written as,
S = (exp)∪(ctr)/t = 4π/t and,
T = (exp)∪(ctr)/s = 4π/s,
where "exp" and "ctr" are expansion and contraction, respectively. The union of the two halves of the 4π scalar cycle is similar to the union of the two halves of the 2π rotation cycle. The expansion from r = 0 to r = √1, and the contraction from r = √1 back to r = 0, is analogous to a rotation of a unit radius, from 0 to 180 degrees, and from 180 degrees back to 0 degrees, in one unit of cycle time, only it requires an equivalent of two 2π rotations to complete one scalar cycle.
Hence, we combine the numerator of the LH term of equation (1) with the numerator of the middle term, and the denominator of the RH term with the denominator of the middle term. Since, the area of the expanding/contracting circle, given by πr2, at time t, is equal to the area swept out by the rotation of the unit radius, measured in radians, there should be a one-to-one correspondence in the quantitative measures of the two motions, though one be scalar and the other vectorial.
In the scalar case, we have a changing area of space over time, with dimensions, s2/t, as a fraction of unit area, analogous to the vectorial case, where we have a changing angle, measured as a fraction of 2π radians, with dimensions t2/s.
The one is the inverse of the other, just as the LST dimensions of mass are the inverse of the dimension of space motion in the ms. In the vectorial case of the LST science, the dimensions are radius (space) times momentum and the quantity is called angular momentum, the basis of Mills atomic model. In the scalar case, however, the dimensions are simply change of area magnitude over time, where no change of position and no mass are involved.
Thus, the angular momentum of LST theory is just the inverse of the 2D velocity of our RSt theory! Therefore, the LST equation for energy, E = hν, or
t/s = t2/s x 1/t (cycles per unit time),
translates to,
s/t = s2/t x 1/s (cycles per unit space),
in our RSt.
Nevertheless, we cannot afford to change the fundamental measure of the LST at this point, just the fundamental understanding. In reality, t/s is scalar motion in time, but it should be understood as a measure of scalar motion in space.
Re: Meeting a Terrific Challenge
As they say, fools rush in, where angels dare not tread. The development of physical theory, using Larson's new system of theory, the RST, requires one to go out on a limb, for sure, risking foolish mistakes that can make one look so incompetent and even ignorant, at times.
Yet, the endeavor, even a misguided one, is a real learning experience, on a level only pioneers can know, and even if it's a painful experience at times, for me it's worth it. One of the things I've discovered by seeking to develop the LRC's RSt, which is a gem of knowledge, is the correspondence between the tetraktys and Larson's cube (LC).
Not only has a means for uniting the discrete numbers of algebra with the analog magnitudes of geometry been found, which is the holy grail for which the LST community is searching so desperately, but also the fact that numbers have only three fundamental properties: magnitude, dimension and "direction."
Each magnitude of a given dimension, and there are only three dimensions, four counting 0, has two "directions," and this marvelous fact is captured in the binary expansion of the tetraktys:

The number two is the number of "directions," or polarities, inherent in the dimension indicated in the number's exponent, which starts at 0, indicating the 0 dimension of a geometric point, the same center point, at the intersection of the three axes of LC.
This is the first level of the tetraktys, at the apex, the beginning of understanding, if you will. We can denote each level as level n, so n = 1 at 20. At n = 2, the dimension 1 is added to dimension 0. At this level, a 20 point and a 21 line correspond to a one-dimensional line in LC, extending in two opposite "directions" from the point.
When n = 3, the dimension 2 is added to the point and the line. This corresponds to a 2D plane, with 22 = 4 "directions," in LC, a plane divided by a line, divided by the center point.
Finally, when n = 4, the dimension 3 is added to the 0, 1 and 2 dimensions, and a 2D plane is extended in two "directions," forming a 3D volume, with 23 = 8 "directions," in LC, a volume divided by three 2D planes, six 1D lines and 1 0D point, at the intersection of them all.
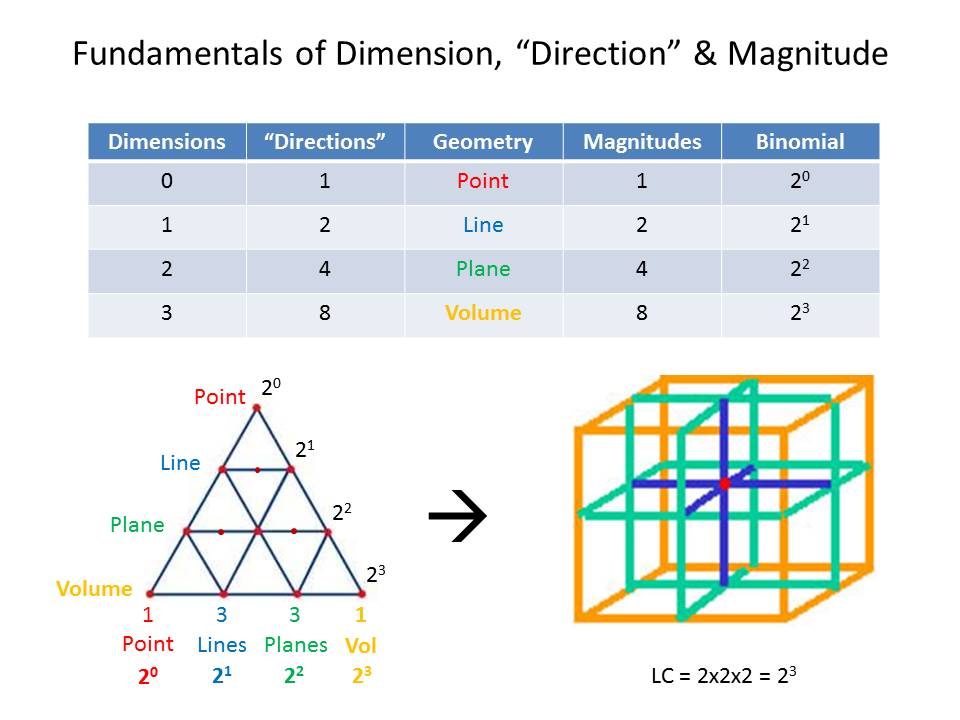
This was a phenomenal discovery for me, when I first realized its implications, years ago. Yet, I didn't realize then just how extensive those implications are, how they extend into the very foundations of the LST science: quantum mechanics and now the GUT of Mills.
Recall that QM employs four so-called quantum numbers, which it uses in the wave equation to generate the spherical harmonics leading to its atomic model with a set of electron orbitals, specifically associated with the spectrum of electron energies observed in the hydrogen atom.
These numbers are the principle quantum number, n, representing the electron's distance from the nucleus, the angular momentum number, L, which determines the shape of the orbital in which the electron may be found, the magnetic number, ml, which determines the orientations of the different orbitals, and the quantum "spin" number, s, which can take two, opposite values. The information is illustrated in the graphic below:

Certain rules apply to the use of these numbers:
But notice how these numbers reflect those of the tetraktys, and thus LC:
When n = 1, L = 0 and m = 0, just as n in the tetraktys equals 20 = 1, a point.
When n = 2, then L = 0, with m = 0 and L = 1, with m = -1, 0 and +1, just as n in the tetraktys = 20 = 1, a point and 21 = 2, a line, in two opposite "directions" from the point. There are three of these two-magnitude sets in LC, one in each of its three dimensions.
When n = 3, L = 0, 1 and 2, each with its set of corresponding m numbers, the latter of which adds m = -2, -1, 0 +1, +2 to the two already existing sets generated by m = 0 and m = 1, just as n = 3 in the tetraktys adds 22 = 4, to the point and the line, with unit magnitude in the four "directions" of its two dimensions.
Finally, when n = 4, as shown below, L = 0, 1, 2 and 3, which adds the seven orbitals of m = -3, -2, -1, 0, 1, 2, 3, to the others, just as n = 4 in the tetraktys = 23 = 8, and adds 8 volumes that can be oriented three ways, in two "directions" along each axis (up and down, left and right, forward and backward), relative to the center point (0), in addition to the four ways along the four diagonal axes, each extending out to corners in two "directions," as shown below:
(Sorry for the over large graphics. Nothing I do in BBcode to resize them works!)
This is a wonderful discovery, but, unfortunately, the wave equation doesn't work very well for QM calculations, because separation of variables becomes a nightmare for calculations involving more than one electron. With Mills' modification, however, which uses the spherical harmonics of the wave equation in a different way, the problem goes away.
This is because he assumes that the proper solution for the wave equation entails the properties of an extended electron, not the impossible point-like, charged structure of QM. The details are complicated and require an understanding of time, radial and angular solutions to the wave equation, but the crux of the matter is that any solution which permits radial motion gives rise to radiation, which would cause the point-like electron to lose energy over time and thus spiral into the nucleus.
However, Mills contends that a function that defines a constant charge density on a spherical shell where
the conditions are right, will cause the classical wave equation,

where ρ(t,x) is changed to ρ(r,θ,φ,t), to represent "the time dependent charge density function of the electron in time and space," to "become a two-dimensional wave equation plus time with separable time and angular functions," whatever that means.
Nevertheless, since there is one condition where the wave equation does not become a 2D wave, that is, it does not propagate as an oscillation over time, that condition can be considered as the ground state of Hydrogen. Thus, asserts Mills, "an electron is a spinning, two-dimensional spherical surface (zero thickness), called an electron orbitsphere ... that can exist in a bound state at only specified distances from the nucleus determined by an energy minimum."
He then goes on to explain how this hollow electron, with this fundamental radius, spins. The spin is due to current loops that produce two, orthogonal and unequal, angular momentum vectors, which give rise to the phenomenon of electron spin.
The explanation Mills gives for this is way over my head, but I notice that as part of it something he calls the orbitsphere current vector field "is rotated clockwise by an angle of π/4 about the z-axis." Well, the fact that the explanation of the quantum "spin" cycle, as a radial 2D space/time oscillation, spanning 4π, in π/4 increments, is our explanation of how that cycle can be equivalent to 4π = 720 degrees of rotation, got my attention.
Not that I'll ever be able to understand Mills' convoluted explanation. Trying to follow his mathematics and the associated technical jargon is enough to kill any interest in the subject, for me. I guess years of fascination with Larson's system of theory has completely spoiled me.
It seems to me that, from the start, the LST community has looked for a way to pair negatively charged electrons, with positively charged protons, in the atoms of the periodic table. What they ended up doing is building a complex set of "compartments," made up of three (four counting zero) dimensions, each with two, opposing "directions," where they could "park" the electrons, packing them into these "rooms," two at a time, paired as males and females would be in hotel room beds.
The trouble is, they had to abandon the established laws of nature to do so, so they did, creating the QM mysteries, and a whole host of inconsistencies and contradictions, hidden from the view of all but the most dedicated specialists, over a period of almost a century.
Now, Mills comes along and blasts it all to kingdom come, as they say, but in the process he transforms the impossible gospel of QM into the impossible gospel of CQM, which replaces the hotel room complex of probability "rooms," built according to the dimensions and the "directions" of the tetraktys and LC architecture, with this expanding/contracting sky of an infinitely thin overcast, surrounding the nucleus, with embedded thunderstorms, full of potential lightening bolts, spinning around the earth-like proton.
For the most part, the LST community is not buying it, and who can blame them? But Mills has the spot-on calculations that QM can't produce, and he has the Suncell. Hence, the proof of the pudding is in the eating, as they say, though you can expect a lot of indigestion, if you are as unprepared for the banquet as I am.
But the big question for us is, "Where does all this leave the RST-based theories, such as the LRC's RSt?" For me, the answer is Larson's answer; The mathematics might work marvelously, but the concepts need clarifying. There are no such things as infinitely thin shells or infinitesimal current loops. The assumption that there are is not a scientific one, and it's philosophically unsatisfying, to say the least.
On the other hand, unless we can calculate observables and predict discoveries as well as Mills can, we are not in much of a position to criticize. I have hopes that we will yet prevail, but I think we will need to follow Mills in abandoning the QM architecture and stick with our scalar model of motions, combinations of motions and relations between them, as an analog of the Bohr model - or the other way around.
If the Bohr (Mills) model of the atom is an analog of our RST-based scalar model, all we have to do is show it.
Ha!
As already pointed out, what Mills does is do away with the hotel room beds of QM and replace them with storm clouds in the proton sky:

In contrast, the positive and negative "charges" of our RSt model are combined together, canceling the effect of one another, while not eliminating the separate entities they belong to, as they do in the case of electron/positron combination.
This is due to the fact that positive "charge" of the proton is a positive imbalance in its space/time ratio of 10/13, while the negative "charge" of the electron is a negative imbalance in its space/time ratio of 6/3. Combined together, they correct each other's imbalance, so the inner term of the combo is (10/13) + (6/3) = 16/16, but without changing the structure of the combo of the two entities into a boson, as the combo would do, if the proton's inner term were 3/6, the inverse of the electron's inner term, as is the positron's.
This gives us a platform onto which we can add bosons, as in the case of Hydrogen, without affecting the intrinsic balance of the two entities in the combo, at least up to a point.

In other words, we don't have to find a place to "park" the electrons in the atom, because they become a part of the same combination of oscillating space and time as the proton, and we don't need to place them in layers of storm clouds in the proton's sky, either, for the same reason!
The good news for us is that Mills has essentially destroyed QM's hold on the LST community, which we never could have done, and he has done this, while leaving the essence of the Bohr model, the Rydberg formula for the atomic spectra of Hydrogen, intact, with which, as I'll discuss in the next post, we happen to have a lot of truck.
Yet, the endeavor, even a misguided one, is a real learning experience, on a level only pioneers can know, and even if it's a painful experience at times, for me it's worth it. One of the things I've discovered by seeking to develop the LRC's RSt, which is a gem of knowledge, is the correspondence between the tetraktys and Larson's cube (LC).
Not only has a means for uniting the discrete numbers of algebra with the analog magnitudes of geometry been found, which is the holy grail for which the LST community is searching so desperately, but also the fact that numbers have only three fundamental properties: magnitude, dimension and "direction."
Each magnitude of a given dimension, and there are only three dimensions, four counting 0, has two "directions," and this marvelous fact is captured in the binary expansion of the tetraktys:

The number two is the number of "directions," or polarities, inherent in the dimension indicated in the number's exponent, which starts at 0, indicating the 0 dimension of a geometric point, the same center point, at the intersection of the three axes of LC.
This is the first level of the tetraktys, at the apex, the beginning of understanding, if you will. We can denote each level as level n, so n = 1 at 20. At n = 2, the dimension 1 is added to dimension 0. At this level, a 20 point and a 21 line correspond to a one-dimensional line in LC, extending in two opposite "directions" from the point.
When n = 3, the dimension 2 is added to the point and the line. This corresponds to a 2D plane, with 22 = 4 "directions," in LC, a plane divided by a line, divided by the center point.
Finally, when n = 4, the dimension 3 is added to the 0, 1 and 2 dimensions, and a 2D plane is extended in two "directions," forming a 3D volume, with 23 = 8 "directions," in LC, a volume divided by three 2D planes, six 1D lines and 1 0D point, at the intersection of them all.

This was a phenomenal discovery for me, when I first realized its implications, years ago. Yet, I didn't realize then just how extensive those implications are, how they extend into the very foundations of the LST science: quantum mechanics and now the GUT of Mills.
Recall that QM employs four so-called quantum numbers, which it uses in the wave equation to generate the spherical harmonics leading to its atomic model with a set of electron orbitals, specifically associated with the spectrum of electron energies observed in the hydrogen atom.
These numbers are the principle quantum number, n, representing the electron's distance from the nucleus, the angular momentum number, L, which determines the shape of the orbital in which the electron may be found, the magnetic number, ml, which determines the orientations of the different orbitals, and the quantum "spin" number, s, which can take two, opposite values. The information is illustrated in the graphic below:

Certain rules apply to the use of these numbers:
- The number n must be a non-zero integer
- The number L must be less than n
- The number ml extends from -L to +L in integer steps
- The number s takes either a positive or negative value

But notice how these numbers reflect those of the tetraktys, and thus LC:
When n = 1, L = 0 and m = 0, just as n in the tetraktys equals 20 = 1, a point.
When n = 2, then L = 0, with m = 0 and L = 1, with m = -1, 0 and +1, just as n in the tetraktys = 20 = 1, a point and 21 = 2, a line, in two opposite "directions" from the point. There are three of these two-magnitude sets in LC, one in each of its three dimensions.
When n = 3, L = 0, 1 and 2, each with its set of corresponding m numbers, the latter of which adds m = -2, -1, 0 +1, +2 to the two already existing sets generated by m = 0 and m = 1, just as n = 3 in the tetraktys adds 22 = 4, to the point and the line, with unit magnitude in the four "directions" of its two dimensions.
Finally, when n = 4, as shown below, L = 0, 1, 2 and 3, which adds the seven orbitals of m = -3, -2, -1, 0, 1, 2, 3, to the others, just as n = 4 in the tetraktys = 23 = 8, and adds 8 volumes that can be oriented three ways, in two "directions" along each axis (up and down, left and right, forward and backward), relative to the center point (0), in addition to the four ways along the four diagonal axes, each extending out to corners in two "directions," as shown below:

(Sorry for the over large graphics. Nothing I do in BBcode to resize them works!)
This is a wonderful discovery, but, unfortunately, the wave equation doesn't work very well for QM calculations, because separation of variables becomes a nightmare for calculations involving more than one electron. With Mills' modification, however, which uses the spherical harmonics of the wave equation in a different way, the problem goes away.
This is because he assumes that the proper solution for the wave equation entails the properties of an extended electron, not the impossible point-like, charged structure of QM. The details are complicated and require an understanding of time, radial and angular solutions to the wave equation, but the crux of the matter is that any solution which permits radial motion gives rise to radiation, which would cause the point-like electron to lose energy over time and thus spiral into the nucleus.
However, Mills contends that a function that defines a constant charge density on a spherical shell where
the conditions are right, will cause the classical wave equation,

where ρ(t,x) is changed to ρ(r,θ,φ,t), to represent "the time dependent charge density function of the electron in time and space," to "become a two-dimensional wave equation plus time with separable time and angular functions," whatever that means.
Nevertheless, since there is one condition where the wave equation does not become a 2D wave, that is, it does not propagate as an oscillation over time, that condition can be considered as the ground state of Hydrogen. Thus, asserts Mills, "an electron is a spinning, two-dimensional spherical surface (zero thickness), called an electron orbitsphere ... that can exist in a bound state at only specified distances from the nucleus determined by an energy minimum."
He then goes on to explain how this hollow electron, with this fundamental radius, spins. The spin is due to current loops that produce two, orthogonal and unequal, angular momentum vectors, which give rise to the phenomenon of electron spin.
The explanation Mills gives for this is way over my head, but I notice that as part of it something he calls the orbitsphere current vector field "is rotated clockwise by an angle of π/4 about the z-axis." Well, the fact that the explanation of the quantum "spin" cycle, as a radial 2D space/time oscillation, spanning 4π, in π/4 increments, is our explanation of how that cycle can be equivalent to 4π = 720 degrees of rotation, got my attention.
Not that I'll ever be able to understand Mills' convoluted explanation. Trying to follow his mathematics and the associated technical jargon is enough to kill any interest in the subject, for me. I guess years of fascination with Larson's system of theory has completely spoiled me.
It seems to me that, from the start, the LST community has looked for a way to pair negatively charged electrons, with positively charged protons, in the atoms of the periodic table. What they ended up doing is building a complex set of "compartments," made up of three (four counting zero) dimensions, each with two, opposing "directions," where they could "park" the electrons, packing them into these "rooms," two at a time, paired as males and females would be in hotel room beds.
The trouble is, they had to abandon the established laws of nature to do so, so they did, creating the QM mysteries, and a whole host of inconsistencies and contradictions, hidden from the view of all but the most dedicated specialists, over a period of almost a century.
Now, Mills comes along and blasts it all to kingdom come, as they say, but in the process he transforms the impossible gospel of QM into the impossible gospel of CQM, which replaces the hotel room complex of probability "rooms," built according to the dimensions and the "directions" of the tetraktys and LC architecture, with this expanding/contracting sky of an infinitely thin overcast, surrounding the nucleus, with embedded thunderstorms, full of potential lightening bolts, spinning around the earth-like proton.
For the most part, the LST community is not buying it, and who can blame them? But Mills has the spot-on calculations that QM can't produce, and he has the Suncell. Hence, the proof of the pudding is in the eating, as they say, though you can expect a lot of indigestion, if you are as unprepared for the banquet as I am.
But the big question for us is, "Where does all this leave the RST-based theories, such as the LRC's RSt?" For me, the answer is Larson's answer; The mathematics might work marvelously, but the concepts need clarifying. There are no such things as infinitely thin shells or infinitesimal current loops. The assumption that there are is not a scientific one, and it's philosophically unsatisfying, to say the least.
On the other hand, unless we can calculate observables and predict discoveries as well as Mills can, we are not in much of a position to criticize. I have hopes that we will yet prevail, but I think we will need to follow Mills in abandoning the QM architecture and stick with our scalar model of motions, combinations of motions and relations between them, as an analog of the Bohr model - or the other way around.
If the Bohr (Mills) model of the atom is an analog of our RST-based scalar model, all we have to do is show it.
Ha!
As already pointed out, what Mills does is do away with the hotel room beds of QM and replace them with storm clouds in the proton sky:

In contrast, the positive and negative "charges" of our RSt model are combined together, canceling the effect of one another, while not eliminating the separate entities they belong to, as they do in the case of electron/positron combination.
This is due to the fact that positive "charge" of the proton is a positive imbalance in its space/time ratio of 10/13, while the negative "charge" of the electron is a negative imbalance in its space/time ratio of 6/3. Combined together, they correct each other's imbalance, so the inner term of the combo is (10/13) + (6/3) = 16/16, but without changing the structure of the combo of the two entities into a boson, as the combo would do, if the proton's inner term were 3/6, the inverse of the electron's inner term, as is the positron's.
This gives us a platform onto which we can add bosons, as in the case of Hydrogen, without affecting the intrinsic balance of the two entities in the combo, at least up to a point.

In other words, we don't have to find a place to "park" the electrons in the atom, because they become a part of the same combination of oscillating space and time as the proton, and we don't need to place them in layers of storm clouds in the proton's sky, either, for the same reason!
The good news for us is that Mills has essentially destroyed QM's hold on the LST community, which we never could have done, and he has done this, while leaving the essence of the Bohr model, the Rydberg formula for the atomic spectra of Hydrogen, intact, with which, as I'll discuss in the next post, we happen to have a lot of truck.
Re: Meeting a Terrific Challenge
Mills modified the Bohr model of the atom, by modifying the LST's model of the electron, changing it from a point-like particle to a shell-like, hollow sphere. At the Hydrogen ground state, it surrounds the proton, forming a cavity, with the so-called Bohr radius (5.2918 e-11 m), in which a photon of 13.6 eV resonates.
The sphere temporarily expands to accommodate higher energy photons, in quantum leaps of energy, where E = hν, and quickly contracts to the ground state, releasing the extra energy as radiation, just as the Bohr model electron does, when it transitions to a lower orbit, as given by the Rydberg formula.
Now, as explained previously, in the atomic model of the LRC's RSt, built from combinations of discrete scalar motions, the scalar motion of the electron combines with the scalar motion of the proton, forming a new entity, the scalar motion of the atom.
In this scalar model, there is no electric cavity to accommodate a photon, and there is no lower or higher orbit for a particle to transition to. The scalar motion of the photon momentarily combines with the scalar motion of the atom, but to understand the RSt scalar motion model quantitatively, we have to understand the basic building block of all these scalar motion entities, the SUDRs and TUDRs (Ss and Ts) of the S|T units.
In order to do this, we need to be able to express the magnitudes of space and time, which constitute the motion, in terms of natural units that can be equated with conventional units. Two attempts have been made to accomplish this, namely Larson's and Borg's, but the results are very different. Larson's natural space unit is 4.558816e-6 cm, while Borg's is 405.1319933e-33 cm, much, much smaller. Larson's natural time unit is 1.520655e-16 sec, Borg's is 1.351374868e-43 sec, again, much, much smaller.
So, which values are the correct ones? There may be many ways to go about investigating this question, but one way that occurs to me is to compare Borg's work to Mills', since Mills has managed to achieve astounding accuracy, when his theoretical calculations are compared to observed values, over a large range of physical phenomena.
One of the most critical magnitudes in Mills' work, if not the most critical, is the Bohr radius, a0, which lies at the heart of his new orbitsphere model of the electron. Recall, that the Louis de Broglie formula,
λ = h/mv,
converts the momentum (quantity of motion) of physical entities into a electromagnetic wavelength, λ, given Planck's constant h. Hence, given the electron's mass and assuming that it orbits the proton in the Hydrogen atom, the velocity that produces the force required to exactly oppose the electrical attraction, between the positive proton and the negative electron, according to the force balance equation, is given by:
v = √Ke e2/mr
Subsequently, with the electron's orbit velocity in hand, the de Broglie wavelength can be calculated, for any orbit. If we then assume that the orbit radius has to accommodate an integer number of these wavelengths, as Bohr did, then everything falls into place for his model. Each electron orbit, numbered from 1 to infinity, is then the label for the Bohr radius of that orbit and the rest is easy, because the Rydberg formula gives the energy differences between the numbered orbits.
So, it's a matter of the electron's velocity, changing from orbit to orbit, or changing its angular momentum from orbit to orbit, which is key, whether it's expressed as the number of integer wavelengths that fit along the orbital path, as Bohr chose to do, or whether it's expressed as the magnitude of the electron's angular momentum, as Mills chooses to do.
However, there is yet another aspect to consider, which affects its momentum, and that is its "spin," as it orbits the proton. Mathematically, in order for the magnitude of the total momentum to come out right for a given quantum of energy associated with a given orbit, the momentum of the electron's "spin" must be included.
This is a big deal, because, if I understand it correctly, Bohr's model doesn't need to deal with this at all, since the radii of its orbits turn out to be much greater than the radii of Mills' orbitspheres, in all but the ground state, where n = 1.
The reason is fascinating. In a nutshell, this big difference is ultimately due to the trapped photon within the orbitsphere, whereas Bohr's model, understandably, doesn't deal with how the electron accommodates absorbed photons. In Mills' model, the electric field of the photon affects the electric field of the proton that the electron "feels," a feature that changes the equation for the Bohr radius, a0,
In Bohr's equation, the radii of the electron orbits are given by, r = nλ/2π, whereas in Mills' equation, the radii of the orbitspheres are given by, r = λ/2π; That is to say, there are n electron wavelengths per 2π cycle in Bohr's model, while there is only 1 electron wavelength per 2π cycle in Mills' model, and, even though they are equivalent, when n =1 (because 12 = 1), they are definitely not equivalent at n ≠ 1.
So, how come, then, both equations work, to accurately calculate the atomic spectra of Hydrogen, one might wonder? The answer is, the two models are mathematically and physically equivalent, even though their radii are not, because Mills' model includes electron spin in the total momentum magnitude of the orbitsphere, compensating for the missing momentum that would be calculated by a greater radius of an orbiting particle!
Bohr wouldn't have had to bother with electron spin, even if he had known about it, because of his hasty assumption (from our historical perspective) that the electronic orbits had to contain an exact number of wavelengths, given the de Broglie and Rydberg formulae.
Mills, choosing the alternative quantum condition that the angular momentum is quantized, instead of the number of wavelengths at a given level of n, an alternative of which Bohr was unaware, until the so-called "new" QM, with its wave equation and its relativistic "solution" came along to reveal the need for quantum spin momentum, along with orbital angular momentum, in order to arrive at the total momentum required by the equations, has pulled off a coup d'etat in the LST community.
Of course, if Mills were to incorporate the angular momentum of electron spin into his calculations, he needed to "find" it in the orbitsphere, which he needed in turn, in order to have a vector motion that wouldn't radiate away its energy, like the point particle would do, if it were really a point particle and not a wave.
Thus, the idea was born of an infinite number of infinitely thin rings of electric currents, some of which are orthogonal to others, producing the spin angular momentum he needed. This is the ad hoc idea, as complicated and controversial as it is, which is revolutionizing the LST's concept of the electron. People hate it, but it works!
Moreover, because of this change from the number of wavelengths that will fit the orbit of a given radius, to the number of units of angular momentum that the orbitsphere of a given radius possesses, and because the trapped photon modifies the effective charge of the positive proton, something else changes, as well.
The wavelength, λ, now dictates the radius of the orbitsphere allowed, instead of the radius of the orbit, dictating the number of wavelengths allowed. In addition, the modification of the proton's electric field, by the interceding photon of one wavelength, trapped in the orbitsphere cavity, introduces a fractional charge, e/n, into the equation, so that not only do n magnitudes of angular-momentum-radii replace n2 wavelength-radii, if you will, but the math then reduces the dimensions of n from two to one, in the process, making fractional values of n possible, which would be impossible otherwise, because any number squared is always equal to 1 or more, never less than 1.
It's not hard to see why Mills' work has generated so much outrage and opposition over the years. Besides being iconoclastic in the extreme, it seems to be a tortured route to get to a new model of the electron, where the relatively large radii required for the multiple wavelengths of Bohr's spinless electrons in orbit are traded off for the much smaller radii allowed for the orbitsphere's multiple units of angular momentum, calculated by the classical wave equation, which includes the angular momentum of the electron's spin, to make it work.
In contrast, the two-dimensional scalar motion of our RSt model, is much simpler and much more straightforward, once one understands the concept of scalar motion. We've been considering it in terms of the 1D, 2D and 3D components of our new scalar math, but years ago I discovered something interesting about the ratio of surface areas associated with each of the radii.
It turns out that the ratio of the inner sphere area (IAs) to the middle sphere area (MAs) and to the outer sphere area (OAs), are integers:
IAs/IAs = 1
MAs/IAs = 2
OAs/IAs = 3
I didn't know what to do with it at the time, but now that we see how Mills has used the surface area of a unit sphere to turn the world of particle physics, atomic physics and more, upside down, it may be that we can see our way clear to quantify the scalar oscillations at last, if we can find the correct magnitudes of the natural units of space and time.
More next time.
The sphere temporarily expands to accommodate higher energy photons, in quantum leaps of energy, where E = hν, and quickly contracts to the ground state, releasing the extra energy as radiation, just as the Bohr model electron does, when it transitions to a lower orbit, as given by the Rydberg formula.
Now, as explained previously, in the atomic model of the LRC's RSt, built from combinations of discrete scalar motions, the scalar motion of the electron combines with the scalar motion of the proton, forming a new entity, the scalar motion of the atom.
In this scalar model, there is no electric cavity to accommodate a photon, and there is no lower or higher orbit for a particle to transition to. The scalar motion of the photon momentarily combines with the scalar motion of the atom, but to understand the RSt scalar motion model quantitatively, we have to understand the basic building block of all these scalar motion entities, the SUDRs and TUDRs (Ss and Ts) of the S|T units.
In order to do this, we need to be able to express the magnitudes of space and time, which constitute the motion, in terms of natural units that can be equated with conventional units. Two attempts have been made to accomplish this, namely Larson's and Borg's, but the results are very different. Larson's natural space unit is 4.558816e-6 cm, while Borg's is 405.1319933e-33 cm, much, much smaller. Larson's natural time unit is 1.520655e-16 sec, Borg's is 1.351374868e-43 sec, again, much, much smaller.
So, which values are the correct ones? There may be many ways to go about investigating this question, but one way that occurs to me is to compare Borg's work to Mills', since Mills has managed to achieve astounding accuracy, when his theoretical calculations are compared to observed values, over a large range of physical phenomena.
One of the most critical magnitudes in Mills' work, if not the most critical, is the Bohr radius, a0, which lies at the heart of his new orbitsphere model of the electron. Recall, that the Louis de Broglie formula,
λ = h/mv,
converts the momentum (quantity of motion) of physical entities into a electromagnetic wavelength, λ, given Planck's constant h. Hence, given the electron's mass and assuming that it orbits the proton in the Hydrogen atom, the velocity that produces the force required to exactly oppose the electrical attraction, between the positive proton and the negative electron, according to the force balance equation, is given by:
v = √Ke e2/mr
Subsequently, with the electron's orbit velocity in hand, the de Broglie wavelength can be calculated, for any orbit. If we then assume that the orbit radius has to accommodate an integer number of these wavelengths, as Bohr did, then everything falls into place for his model. Each electron orbit, numbered from 1 to infinity, is then the label for the Bohr radius of that orbit and the rest is easy, because the Rydberg formula gives the energy differences between the numbered orbits.
So, it's a matter of the electron's velocity, changing from orbit to orbit, or changing its angular momentum from orbit to orbit, which is key, whether it's expressed as the number of integer wavelengths that fit along the orbital path, as Bohr chose to do, or whether it's expressed as the magnitude of the electron's angular momentum, as Mills chooses to do.
However, there is yet another aspect to consider, which affects its momentum, and that is its "spin," as it orbits the proton. Mathematically, in order for the magnitude of the total momentum to come out right for a given quantum of energy associated with a given orbit, the momentum of the electron's "spin" must be included.
This is a big deal, because, if I understand it correctly, Bohr's model doesn't need to deal with this at all, since the radii of its orbits turn out to be much greater than the radii of Mills' orbitspheres, in all but the ground state, where n = 1.
The reason is fascinating. In a nutshell, this big difference is ultimately due to the trapped photon within the orbitsphere, whereas Bohr's model, understandably, doesn't deal with how the electron accommodates absorbed photons. In Mills' model, the electric field of the photon affects the electric field of the proton that the electron "feels," a feature that changes the equation for the Bohr radius, a0,
In Bohr's equation, the radii of the electron orbits are given by, r = nλ/2π, whereas in Mills' equation, the radii of the orbitspheres are given by, r = λ/2π; That is to say, there are n electron wavelengths per 2π cycle in Bohr's model, while there is only 1 electron wavelength per 2π cycle in Mills' model, and, even though they are equivalent, when n =1 (because 12 = 1), they are definitely not equivalent at n ≠ 1.
So, how come, then, both equations work, to accurately calculate the atomic spectra of Hydrogen, one might wonder? The answer is, the two models are mathematically and physically equivalent, even though their radii are not, because Mills' model includes electron spin in the total momentum magnitude of the orbitsphere, compensating for the missing momentum that would be calculated by a greater radius of an orbiting particle!
Bohr wouldn't have had to bother with electron spin, even if he had known about it, because of his hasty assumption (from our historical perspective) that the electronic orbits had to contain an exact number of wavelengths, given the de Broglie and Rydberg formulae.
Mills, choosing the alternative quantum condition that the angular momentum is quantized, instead of the number of wavelengths at a given level of n, an alternative of which Bohr was unaware, until the so-called "new" QM, with its wave equation and its relativistic "solution" came along to reveal the need for quantum spin momentum, along with orbital angular momentum, in order to arrive at the total momentum required by the equations, has pulled off a coup d'etat in the LST community.
Of course, if Mills were to incorporate the angular momentum of electron spin into his calculations, he needed to "find" it in the orbitsphere, which he needed in turn, in order to have a vector motion that wouldn't radiate away its energy, like the point particle would do, if it were really a point particle and not a wave.
Thus, the idea was born of an infinite number of infinitely thin rings of electric currents, some of which are orthogonal to others, producing the spin angular momentum he needed. This is the ad hoc idea, as complicated and controversial as it is, which is revolutionizing the LST's concept of the electron. People hate it, but it works!
Moreover, because of this change from the number of wavelengths that will fit the orbit of a given radius, to the number of units of angular momentum that the orbitsphere of a given radius possesses, and because the trapped photon modifies the effective charge of the positive proton, something else changes, as well.
The wavelength, λ, now dictates the radius of the orbitsphere allowed, instead of the radius of the orbit, dictating the number of wavelengths allowed. In addition, the modification of the proton's electric field, by the interceding photon of one wavelength, trapped in the orbitsphere cavity, introduces a fractional charge, e/n, into the equation, so that not only do n magnitudes of angular-momentum-radii replace n2 wavelength-radii, if you will, but the math then reduces the dimensions of n from two to one, in the process, making fractional values of n possible, which would be impossible otherwise, because any number squared is always equal to 1 or more, never less than 1.
It's not hard to see why Mills' work has generated so much outrage and opposition over the years. Besides being iconoclastic in the extreme, it seems to be a tortured route to get to a new model of the electron, where the relatively large radii required for the multiple wavelengths of Bohr's spinless electrons in orbit are traded off for the much smaller radii allowed for the orbitsphere's multiple units of angular momentum, calculated by the classical wave equation, which includes the angular momentum of the electron's spin, to make it work.
In contrast, the two-dimensional scalar motion of our RSt model, is much simpler and much more straightforward, once one understands the concept of scalar motion. We've been considering it in terms of the 1D, 2D and 3D components of our new scalar math, but years ago I discovered something interesting about the ratio of surface areas associated with each of the radii.
It turns out that the ratio of the inner sphere area (IAs) to the middle sphere area (MAs) and to the outer sphere area (OAs), are integers:
IAs/IAs = 1
MAs/IAs = 2
OAs/IAs = 3
I didn't know what to do with it at the time, but now that we see how Mills has used the surface area of a unit sphere to turn the world of particle physics, atomic physics and more, upside down, it may be that we can see our way clear to quantify the scalar oscillations at last, if we can find the correct magnitudes of the natural units of space and time.
More next time.
Re: Meeting a Terrific Challenge
The amazing feat of Mills (some call it sleight of hand), is that he traded the relatively large radii of orbiting point masses, for much smaller radii of circulating charge currents. His trade-off keeps the forces balanced between the outward angular momentum vector of the orbitsphere and the inward charge vector of the proton, the trapped photon and the electron, so the end result is the same for both the Bohr and the Mills models of the Hydrogen atom, because the forces balance. They just balance in different ways.
As a result, the Rydberg energy formula,
ΔE = Re(1/nf2 - 1/ni2) ..............................(1)
applies equally to both models, even though one employs orbiting point masses, at large radii, and the other a large number (actually an infinite number) of circulating charge currents, at much smaller radii. The difference is that, with Mills' model, fractional n states are possible, leading to the hydrino phenomenon. Of course, this is not all. With Mills' model, the frequency spectra of multi-electron atoms can be calculated as well, whereas they cannot with Bohr's model, showing the superiority, if not the validation, of Mills' choice of angular momentum, as the theoretical "quantization condition."
At first blush, it would seem that quantized angular momentum only makes sense in a vector motion model of the atom, where momentum, as the velocity of a mass, is clearly understood, as part of our human experience, but when we stop to think in terms of the space and time dimensions of oscillating scalar motion, there is a corollary. For instance, the scalar motion of two, 3D volumes, oscillating as reciprocals, with expanding/contracting radii, would also have the dimensions of momentum, even though no mass is moving.
In our scalar motion equation,
S|T = 1/2 + 1/1 + 2/1 = 4|4, ......................................................(2)
the number of inward and outward cycle halves are tallied separately for two scalar oscillations, one in space and one in time. We don't often think about it, but each of these oscillations is synonymous with the equation for vector rotation, where four .5π rotations are combined into 1 (4/4) unit of 2π rotation to represent a sine wave, where one fourth of the rotation is equated to one fourth the circumference of the unit circle. The sine wave changes "directions" four times over one cycle, but the analogous rotation is thought of as a unidirectional vector motion of rotation.
Years ago, Bob Palais, math prof at the UofU, attended one of our ISUS meetings in SLC. He related his frustration with the lack of fundamental understanding of Freshman students, regarding the sine wave and the unit circle. "I was wondering why students didn't realize π/2 was a quarter of the way around the unit circle , so that (cos(π/2), sin(π/2)) = (0, 1), and suddenly the disconnect between the half and the quarter forced me to realize that it wasn't their fault, it was ours. π was wrong!"
What he meant, of course, is that, while the diameter of the unit circle times π gives us the circumference of the circle, working with the diameter of the unit circle won't do, for many reasons. So, science uses the radius and the diameter, as twice the radius, and writes it as, 2πr, which is the same thing. Yet, somehow most high school students miss the "sleight of hand." involved.
Here's a well-done, entertaining, but short video, explaining the confusion: Pi is (still) wrong
However, what I wish I could have explained to Bob at the time, but didn't, because I didn't understand it then, is that we don't have to resort to sines and cosines to understand waves! A radial wave propagates out to the circumference of the unit circle, and its expansion can be understood as scalar motion in 1/4 π segments of an area of 2π magnitude, equivalent to the rotation around the circumference of the complex plane, by virtue of imaginary numbers, yet it has nothing to do with rotation and angles.
(Correction: The 2D magnitude is, of course, πr2, which would be π for the unit circle, and 2π for the full expansion/contraction cycle. The corrections are noted below in brackets.)
The kicker, though, is that the 2π [π] propagation of the wave over time is only one-half of the cycle. It's just that we've never seen a wave return from the circumference to its point of origin, except when we "run time backwards" in a movie of a wave. Even today, Bob could invite the entire University of Utah to attend a presentation on why quantum "spin" must be a 4π cycle and not a 2π cycle and astound them, because they are taught that nobody understands how this 4π cycle can be. [i.e. one 2D oscillation cycle is equivalent to two 1D rotation cycles.]
This is the huge disconnect between us and the LST community. We know that the scalar increase/decrease of area, or volume, over time, is just as much a form of motion as is the increase/decrease of linear distance, or linear trips around a unit circle's circumference, over time.
Scalar motion is indeed a neglected fact of science, among many that Larson has pointed out. Fortunately, we can reformulate our equation (2) to reflect the truth of multi-dimensional motion:
v1 = s+s/2t = 2s1/2t .....................................................................(3)
v2 = s2+s2/2t = 2s2/2t .....................................................................(4)
v3 = s3+s3/2t = 2s3/2t .....................................................................(5)
Now, we understand the coefficient 2 in the numerator of these equations, as the two halves of the 4π [2π] cycle (outward 2π [π] and inward 2π [π]), but what about the coefficient in the denominator? Why two units of time in the denominator? Well, this clears up another easily overlooked fact that is obscured by the rotation regime.
When the sine wave crosses over the datum, from a decreasing positive "direction," to an increasing negative "direction," half-way through its cycle, one unit of time has expired. We might say it's a "space of time" equal to π, because, without a change in "direction," at the 0 crossover point, we would measure the motion in units of space per units of time, in a one-to-one ratio, what we call "unit speed." Only when a change of "direction" is involved, as in oscillation, do we require two units of time; i.e. one unit of time for the motion in each "direction" (outward/inward).
However, in terms of a unit circumference, or one revolution of the complex plane, these two units of time are considered as one. The motion of rotation, and thus the wave, is measured in terms of one unit of circumference per "unit" of time, obscuring the true measure of two units of space per two units of time.
With this much understood, the question for us is how do we translate these fundamentals, based on vector motion and its associated calculus and algebra and geometry, into our scalar motion paradigm, where the one-dimensional science of the LST is replaced by the multi-dimensional science of the RST?
I wish I were smart enough to do the translation in a straightforward, easy to understand manner, but it's all I can do to understand the beautiful mathematics involved. If I understand it correctly, though, the key is still in the Euler formula,
eπi = -1, and ..........................................................(6)
(eπi)2 = (-1)2 = 1 .................................................(7)
It just so happens that, because exponents, properly understood, are actually members of what's called the additive group of numbers and their resultants are in the multiplicative group (i.e. nx+y = nx x ny), a transformation takes place from the additions on the grid of the complex plane to rotations of radius one on the complex plane. What this means is that, since any real number, n, raised to any real exponent, x, is positive, the change in magnitude is a scalar change of real magnitude, but doing the same thing with complex numbers, results in rotations on the unit circle of the complex plane.
Consequently, the number e, when raised to a power of 'πi', is equivalent to a rotation of π radians, which can be thought of as a rotation from a real positive 1, to a real negative 1, on the real number line of the complex plane, as explained in this short video clip. The full clip can be viewed here
But, by the same token, e raised to a power of πi, is equal to one half the area of the unit circle (π radians), which cannot only be seen as "a walk half-way around the unit circle," but also as an expansion of area to half the unit circle.
Equation (6), is very useful as a rotation, from +1 to -1, on the circumference, but it's really an infinite addition of areas that produces the rotation. Subsequently squaring it, we get:
(eπi)2 = eπi+πi = e2πi = 1,
rotating us back to positive one on the coordinate grid, sure enough, but in reality doubling the area of the half circle, from π radians to 2π radians.
Of course, this mathematical truth is arguably the foundation of everything electronic in our modern world, because it can be used as a "number that spins," due to the fact that,
eiθ = cos θ + i sin θ, and
e-iθ = cos θ - i sin θ,
where θ is the changing angle of the unit circle's radius.
On the unit circle, the square root of the sum of the squares applies for the radius, so that (cos2 θ + sin2 θ) = |(eiθ)|2 = 1.
Hence, for any value of the angle θ, the radius of the unit circle on the complex plane will always be 1, as expressed by |eiθ|, and i is a multiplier of the angle θ. What this amounts to is that the value e, the "complex exponential" as it's called, can be used as concise notation for the set of complex numbers on the unit circle on the complex plane.
Consequently, when we continuously increase the angle θ, over time, the complex exponential rotates around the unit circle. In electronics and signal processing, as well as physics, this is done by replacing the angle θ, in the complex exponential, with ωt, where ω is the frequency of change (2π rotation per second) and t is the unit of time, seconds.
However, this neat little trick is ultimately possible, because the variable cos θ is equal to one half the sum of two, opposite area expansions, 1/2(eiθ + e-iθ) (see this derived here at about time mark 5:20). So, what if we didn't use the complex exponential to cycle around the 2π [radian] circumference of the unit circle, but instead used it to expand the 0 point out to the 2π [π] area of the unit circle, and contract it back again? Or better yet, used it to expand/contract the 4π area of the unit sphere? Is that possible?
More on this next time.
As a result, the Rydberg energy formula,
ΔE = Re(1/nf2 - 1/ni2) ..............................(1)
applies equally to both models, even though one employs orbiting point masses, at large radii, and the other a large number (actually an infinite number) of circulating charge currents, at much smaller radii. The difference is that, with Mills' model, fractional n states are possible, leading to the hydrino phenomenon. Of course, this is not all. With Mills' model, the frequency spectra of multi-electron atoms can be calculated as well, whereas they cannot with Bohr's model, showing the superiority, if not the validation, of Mills' choice of angular momentum, as the theoretical "quantization condition."
At first blush, it would seem that quantized angular momentum only makes sense in a vector motion model of the atom, where momentum, as the velocity of a mass, is clearly understood, as part of our human experience, but when we stop to think in terms of the space and time dimensions of oscillating scalar motion, there is a corollary. For instance, the scalar motion of two, 3D volumes, oscillating as reciprocals, with expanding/contracting radii, would also have the dimensions of momentum, even though no mass is moving.
In our scalar motion equation,
S|T = 1/2 + 1/1 + 2/1 = 4|4, ......................................................(2)
the number of inward and outward cycle halves are tallied separately for two scalar oscillations, one in space and one in time. We don't often think about it, but each of these oscillations is synonymous with the equation for vector rotation, where four .5π rotations are combined into 1 (4/4) unit of 2π rotation to represent a sine wave, where one fourth of the rotation is equated to one fourth the circumference of the unit circle. The sine wave changes "directions" four times over one cycle, but the analogous rotation is thought of as a unidirectional vector motion of rotation.
Years ago, Bob Palais, math prof at the UofU, attended one of our ISUS meetings in SLC. He related his frustration with the lack of fundamental understanding of Freshman students, regarding the sine wave and the unit circle. "I was wondering why students didn't realize π/2 was a quarter of the way around the unit circle , so that (cos(π/2), sin(π/2)) = (0, 1), and suddenly the disconnect between the half and the quarter forced me to realize that it wasn't their fault, it was ours. π was wrong!"
What he meant, of course, is that, while the diameter of the unit circle times π gives us the circumference of the circle, working with the diameter of the unit circle won't do, for many reasons. So, science uses the radius and the diameter, as twice the radius, and writes it as, 2πr, which is the same thing. Yet, somehow most high school students miss the "sleight of hand." involved.
Here's a well-done, entertaining, but short video, explaining the confusion: Pi is (still) wrong
However, what I wish I could have explained to Bob at the time, but didn't, because I didn't understand it then, is that we don't have to resort to sines and cosines to understand waves! A radial wave propagates out to the circumference of the unit circle, and its expansion can be understood as scalar motion in 1/4 π segments of an area of 2π magnitude, equivalent to the rotation around the circumference of the complex plane, by virtue of imaginary numbers, yet it has nothing to do with rotation and angles.
(Correction: The 2D magnitude is, of course, πr2, which would be π for the unit circle, and 2π for the full expansion/contraction cycle. The corrections are noted below in brackets.)
The kicker, though, is that the 2π [π] propagation of the wave over time is only one-half of the cycle. It's just that we've never seen a wave return from the circumference to its point of origin, except when we "run time backwards" in a movie of a wave. Even today, Bob could invite the entire University of Utah to attend a presentation on why quantum "spin" must be a 4π cycle and not a 2π cycle and astound them, because they are taught that nobody understands how this 4π cycle can be. [i.e. one 2D oscillation cycle is equivalent to two 1D rotation cycles.]
This is the huge disconnect between us and the LST community. We know that the scalar increase/decrease of area, or volume, over time, is just as much a form of motion as is the increase/decrease of linear distance, or linear trips around a unit circle's circumference, over time.
Scalar motion is indeed a neglected fact of science, among many that Larson has pointed out. Fortunately, we can reformulate our equation (2) to reflect the truth of multi-dimensional motion:
v1 = s+s/2t = 2s1/2t .....................................................................(3)
v2 = s2+s2/2t = 2s2/2t .....................................................................(4)
v3 = s3+s3/2t = 2s3/2t .....................................................................(5)
Now, we understand the coefficient 2 in the numerator of these equations, as the two halves of the 4π [2π] cycle (outward 2π [π] and inward 2π [π]), but what about the coefficient in the denominator? Why two units of time in the denominator? Well, this clears up another easily overlooked fact that is obscured by the rotation regime.
When the sine wave crosses over the datum, from a decreasing positive "direction," to an increasing negative "direction," half-way through its cycle, one unit of time has expired. We might say it's a "space of time" equal to π, because, without a change in "direction," at the 0 crossover point, we would measure the motion in units of space per units of time, in a one-to-one ratio, what we call "unit speed." Only when a change of "direction" is involved, as in oscillation, do we require two units of time; i.e. one unit of time for the motion in each "direction" (outward/inward).
However, in terms of a unit circumference, or one revolution of the complex plane, these two units of time are considered as one. The motion of rotation, and thus the wave, is measured in terms of one unit of circumference per "unit" of time, obscuring the true measure of two units of space per two units of time.
With this much understood, the question for us is how do we translate these fundamentals, based on vector motion and its associated calculus and algebra and geometry, into our scalar motion paradigm, where the one-dimensional science of the LST is replaced by the multi-dimensional science of the RST?
I wish I were smart enough to do the translation in a straightforward, easy to understand manner, but it's all I can do to understand the beautiful mathematics involved. If I understand it correctly, though, the key is still in the Euler formula,
eπi = -1, and ..........................................................(6)
(eπi)2 = (-1)2 = 1 .................................................(7)
It just so happens that, because exponents, properly understood, are actually members of what's called the additive group of numbers and their resultants are in the multiplicative group (i.e. nx+y = nx x ny), a transformation takes place from the additions on the grid of the complex plane to rotations of radius one on the complex plane. What this means is that, since any real number, n, raised to any real exponent, x, is positive, the change in magnitude is a scalar change of real magnitude, but doing the same thing with complex numbers, results in rotations on the unit circle of the complex plane.
Consequently, the number e, when raised to a power of 'πi', is equivalent to a rotation of π radians, which can be thought of as a rotation from a real positive 1, to a real negative 1, on the real number line of the complex plane, as explained in this short video clip. The full clip can be viewed here
But, by the same token, e raised to a power of πi, is equal to one half the area of the unit circle (π radians), which cannot only be seen as "a walk half-way around the unit circle," but also as an expansion of area to half the unit circle.
Equation (6), is very useful as a rotation, from +1 to -1, on the circumference, but it's really an infinite addition of areas that produces the rotation. Subsequently squaring it, we get:
(eπi)2 = eπi+πi = e2πi = 1,
rotating us back to positive one on the coordinate grid, sure enough, but in reality doubling the area of the half circle, from π radians to 2π radians.
Of course, this mathematical truth is arguably the foundation of everything electronic in our modern world, because it can be used as a "number that spins," due to the fact that,
eiθ = cos θ + i sin θ, and
e-iθ = cos θ - i sin θ,
where θ is the changing angle of the unit circle's radius.
On the unit circle, the square root of the sum of the squares applies for the radius, so that (cos2 θ + sin2 θ) = |(eiθ)|2 = 1.
Hence, for any value of the angle θ, the radius of the unit circle on the complex plane will always be 1, as expressed by |eiθ|, and i is a multiplier of the angle θ. What this amounts to is that the value e, the "complex exponential" as it's called, can be used as concise notation for the set of complex numbers on the unit circle on the complex plane.
Consequently, when we continuously increase the angle θ, over time, the complex exponential rotates around the unit circle. In electronics and signal processing, as well as physics, this is done by replacing the angle θ, in the complex exponential, with ωt, where ω is the frequency of change (2π rotation per second) and t is the unit of time, seconds.
However, this neat little trick is ultimately possible, because the variable cos θ is equal to one half the sum of two, opposite area expansions, 1/2(eiθ + e-iθ) (see this derived here at about time mark 5:20). So, what if we didn't use the complex exponential to cycle around the 2π [radian] circumference of the unit circle, but instead used it to expand the 0 point out to the 2π [π] area of the unit circle, and contract it back again? Or better yet, used it to expand/contract the 4π area of the unit sphere? Is that possible?
More on this next time.
Re: Meeting a Terrific Challenge
Somehow, in the comment above, I started thinking of the area formula as A = 2πr2, instead of correct equation, A = πr2. Sorry for the confusion. I've edited the OP to show the necessary corrections in brackets.