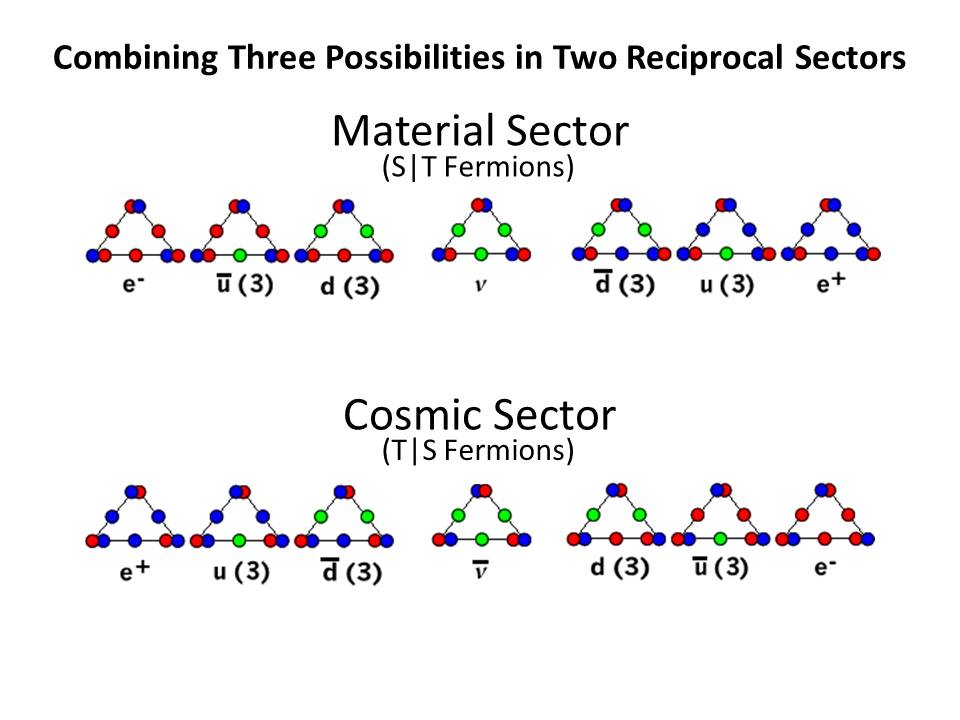
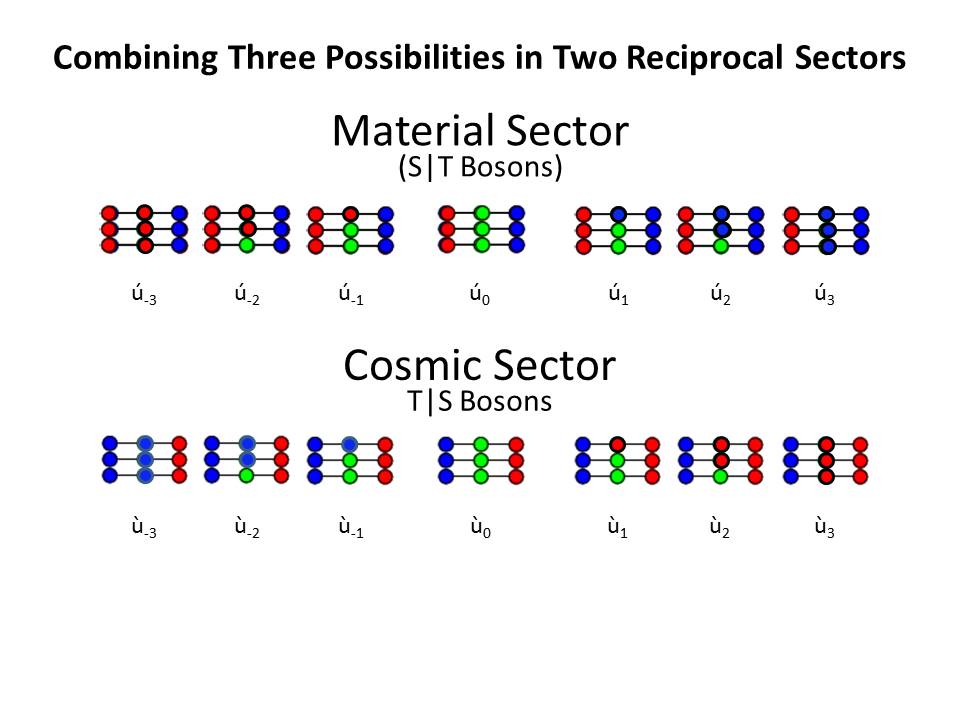
Recall that the reason we want to do this is that we want to translate the vector motion of the LST, as used in the model of the atom, to the scalar motion of the LRC's RST-based model of the atom, which has no vector motion, but consists of strictly scalar motion.
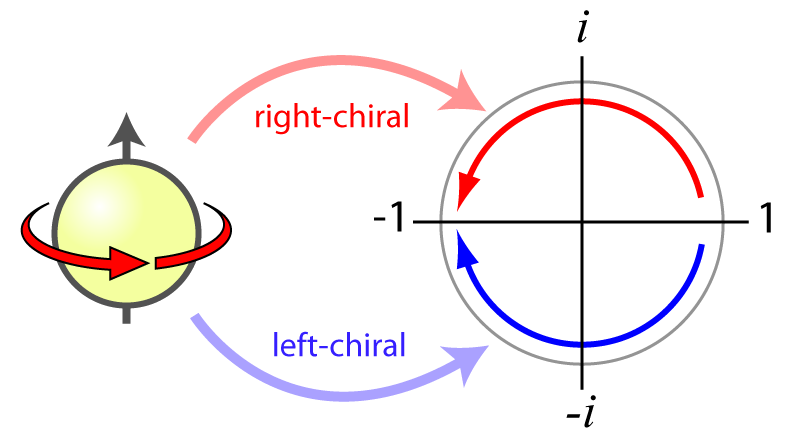
We want to use the "complex exponential," eπi = -1, because it consists of the sum of the cosine and i times the sine, of the angle θ. This is very useful for reconstructing a sine or cosine wave over time, but it's also applicable to the scalar motion expansion/contraction of the RSt's S|T unit, since the sine and cosine of angle θ are orthogonal and thus reciprocal magnitudes, as are the S and T oscillations of the S|T unit.
However, the ratio between the angles of the right triangle, upon which the sine and cosine are based, produce four changes of sign (polarity) as the angle θ grows from 0 to 90, 90 to 180, 180 to 270 and 270 to 360 degrees, each of which are associated with the four quadrantal rotations (4 x π/2). What we want are two changes of sign (a change equivalent to a rotation from 0 to 180, and from 180 to 360), as the sphere expands and contracts, over π, in each "direction."
This requires us to view the complex exponential, eiωt, from a new perspective. Instead of viewing it as the 2π rotation cycle in the positive direction, and its negative form, e-iωt, as the 2π rotation cycle in the negative direction, where their sum is divided by 2, i.e. ((eiωt) + (e-iωt))/2, to extract cos(ωt), we should view the same thing as a 2 x π = 2π expansion/contraction cycle, over two, 2π rotations.
Of course, there is an important distinction that remains to be made between scalar motion and vector motion: Scalar motion expands/contracts in all the "directions" of a given dimension simultaneously, while vector motion changes location in one "direction" at a time.
In one dimension of scalar motion, an oscillating length for example, there are two "directions" involved (positive and negative). Therefore, the scalar expansion/contraction of the 1D diameter takes place in these two opposite "directions," relative to the point of origin. So, one cycle of 1D oscillation involves expansion/contraction along four lengths of "radii," if you will: one in each of two opposite "directions," when expanding outward, and one in each of two opposite "directions," when contracting inward.
In two dimensions of scalar motion, as in the area of the circle, however, there are four "directions" (two positive and two negative). Therefore, the scalar expansion/contraction of the area takes place in these four opposing "directions" (quadrants) relative to the point of origin. The motion takes place in all of them simultaneously. So, one full cycle, involves motion over eight "radii," if you will: over four when expanding outward and back over the same four when contracting inward.
The corresponding 1D vector motion, on the other hand, always moves a point along the length of the radius, one "direction" at a time: For example, it extends outward one positive unit, retracts inward one positive unit, extends outward one negative unit and retracts inward one negative unit, every cycle. Moreover, vector motion in more than one dimension at a time is impossible, even though separate motions in more than one dimension, may be combined, as they are in the case of the sine and cosine of eiθ, which is actually the rotation of a complex number of magnitude one.
Vector motion along the x axis, composed of 1/2(eiθ) and 1/2(e-iθ), when the angle θ changes over time, as ωt, is shown here, as the vector sum of two opposite vector rotations. This vector sum transits the unit radius, four times per cycle, in and out, in two opposite "directions."
I wish I could produce a similar video for the corresponding motion of the changing scalar area, but I'll have to settle for a crude animated gif to show the comparison. First, I have to explain, though, that the reason the correspondence between the 1D vector motion of rotation and the 2D scalar motion of oscillation exists is that the unit of 2π radians of the unit circle is actually a dimensionless number, which can be derived from both a 1D length and a 2D area.
The dimension of the arc length of the 2π radians along the circumference, which is used to define the radian, is, of course, the same as the dimension of the 1D radius, while the dimensions of the area sector determined by the 1D arcs are obviously the same as the area of the circle. Thus, at the unit magnitude of r, the disparity in dimensions makes no difference, and the magnitude of the rotation is simply twice that of the expansion/contraction; that is, the rotation cycle is 2π versus the 1π expansion cycle.
2πr/r = 2π and πr2/r2 = π.
Consequently, given that the complex exponential, eπi, is equal to π radians, it is also equal to the number of area units of the expanded circle, but these units have different dimensions. In terms of rotating around the circle, the complex exponential is only half way around it, at π radians. To complete one revolution of the circle, it must rotate another π radians, thus taking two π, 1D radians of rotation, to "paint" one π, 2D radians of area, if you will.
I know that it is so much more precise and scientific to explain all this in terms of the functions of calculus, which people are used to seeing, but, for me, that approach is tantamount to taking the long way around. The simple truth we need to grasp is that the ratio of the circle's area to its circumference is 1:2. Thus, the rotation around the unit circle's circumference is a distance twice the magnitude of the area of the corresponding sector that the unit radius sweeps, and, since we know that the complex exponential, in its ωt form, rotates the angle θ of the unit radius, we can think of the vector rotation, as driving the scalar oscillation (or even vice versa), as shown in the animated gif below:
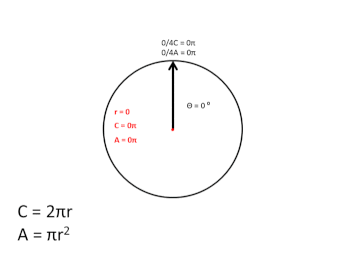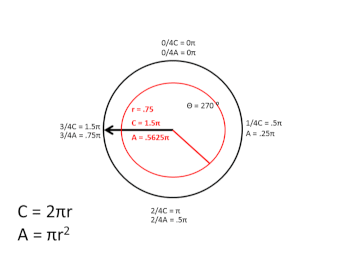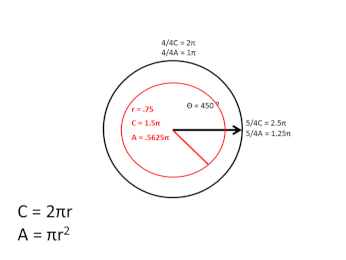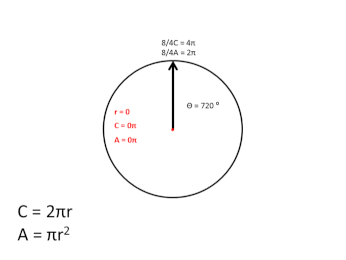
In the graphic above, I didn't follow the usual convention used, when plotting the sine/cosine of angle θ, by starting at 90 degrees and increasing counter-clockwise, but instead I started at 0 degrees, proceeding clockwise around the circle, and, as the graphic shows, as the angle increases, the magnitude of the 1D arc of the black circle's circumference that is transited to that point is equal to the entire circumference of the red expanding circle, during the first, 2π, rotation cycle. During the second, 2π, rotation cycle, the red circle contracts back to zero, completing one full scalar cycle.
However, since there are two, reciprocal oscillations that constitute the S|T unit, one space oscillation and one time oscillation, the associated, inverse rotation of the view of the rotation shown in the graphic above, occurs on the other side of the circle, which if we turned it around, would be rotating in the counter-clockwise "direction."
The result would be two, inverse, scalar oscillations. One is fully expanded at the beginning of the two rotation cycles, while the other is fully contracted at the beginning:
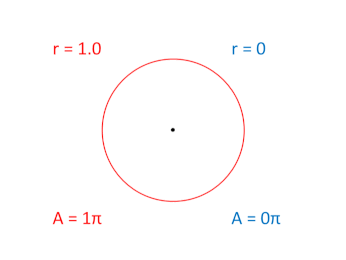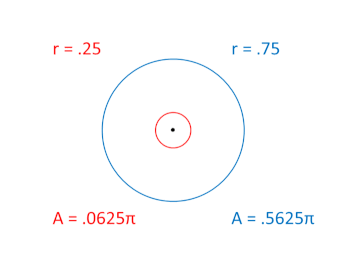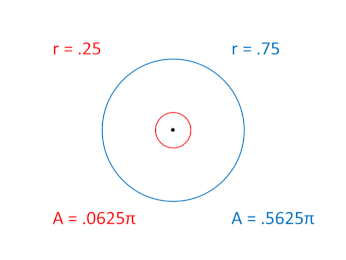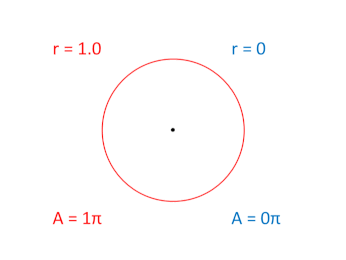
The two, 2π rotation cycles associated with these two scalar expansions are not shown in this graphic, but if we were to show them side by side, one would be rotating around the unit circle in the clockwise "direction" while the other would be rotating in the counter-clockwise "direction."
The bottom line is to show that there is a correspondence between the vector motion of the LST's complex exponential, eiωt, with its inverse, e-iωt, and the two, inverse scalar oscillations of the S|T unit.
Of course, the oscillations of the S|T unit are three dimensional volume oscillations, but they can be characterized by any of their dimensional components. In this case, the 2D scalar motion is isomorphic to the LST's 2D vector motion known as a "quantity of motion," or more commonly, momentum, even though no mass or vector velocity is involved.
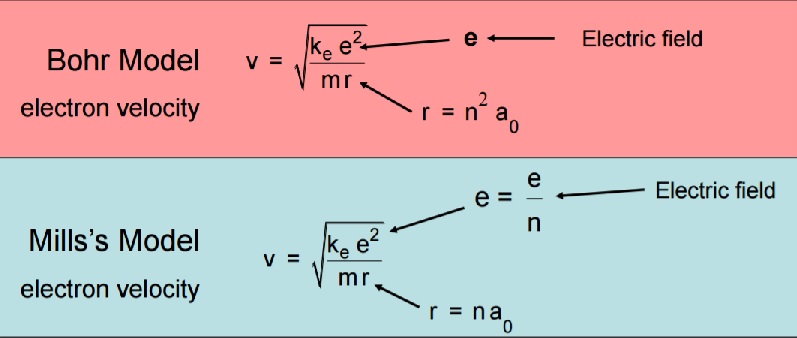
This is important for our theoretical development, since in our model of the atom, the space-like (negative) oscillation of the electron combines with the time-like (positive) oscillation of the proton, and there is no separation between the two, such as the all important Bohr radius in the LST model, which gives rise either to an orbiting point charge in the Bohr model, or a set of circulating electric currents in Mills' modification of the Bohr model.
With this much understood, we need to show that the 2D scalar motion of our model can be seen as the equivalent to the angular momentum of Mills' model, which will hopefully enable us to construct a scalar motion model of the atom as successful as his is.